
7一阶电路和二阶电路的时域分析 7-1动态电路的方程及其初始条件 7-2一阶电路的零输入响应 7-3一阶电路的零状态响应 7-4一阶电路的全响应 7-5二阶电路的零输入响应 7-6二阶电路的零状态响应和全响应 7-7一阶电路和二阶电路的阶跃响应 7-8一阶电路和二阶电路的冲激响应 7-10状方程
7 ж䱬⭫䐥ૂӂ䱬⭫䐥Ⲻᰬต࠼᷆ 7-3 а䱦⭥䐟Ⲵ䴦⣦ᘱ૽ᓄ 7-5 Ҽ䱦⭥䐟Ⲵ䴦䗃ޕ૽ᓄ 7-6 Ҽ䱦⭥䐟Ⲵ䴦⣦ᘱ૽ᓄ઼ޘ૽ᓄ 7-7 а䱦⭥䐟઼Ҽ䱦⭥䐟Ⲵ䱦䏳૽ᓄ 7-2 а䱦⭥䐟Ⲵ䴦䗃ޕ૽ᓄ 7-4 а䱦⭥䐟Ⲵޘ૽ᓄ 7-1 ࣘᘱ⭥䐟Ⲵᯩ〻৺ަࡍᶑԦ 7-8 а䱦⭥䐟઼Ҽ䱦⭥䐟Ⲵߢ૽◰ᓄ 7-10 ⣦ᘱᯩ〻

7-1动态电路的方程及其初始条件 一、动态电路(transient circuit). 动态电路:含有电容、电感的电路称为动态电路。 电容C、电感L一动态元件 动态电路的分析求解: 第7章一经典法时域分析法(低阶动态电路) 第14章一运算法1复频域分析法(高阶动态电路)
7-1 ࣞᘷ⭫䐥ⲺᯯぁެࡓခᶗԬ ࣘᘱ⭥䐟Ⲵ࠶≳᷀䀓˖ ㅜ7ㄐ——㓿ި⌅\ᰦฏ࠶˄⌅᷀վ䱦ࣘᘱ⭥䐟˅ ㅜ14ㄐ——䘀㇇⌅\༽仁ฏ࠶˄⌅᷀儈䱦ࣘᘱ⭥䐟˅ ࣘᘱ⭥䐟˖ਜ਼ᴹ⭥ᇩǃ⭥ᝏⲴ⭥䐟〠Ѫࣘᘱ⭥䐟DŽ ⭥ᇩCǃ⭥ᝏL——ࣘᘱݳԦ аǃࣘᘱ⭥䐟˄transient circuit˅
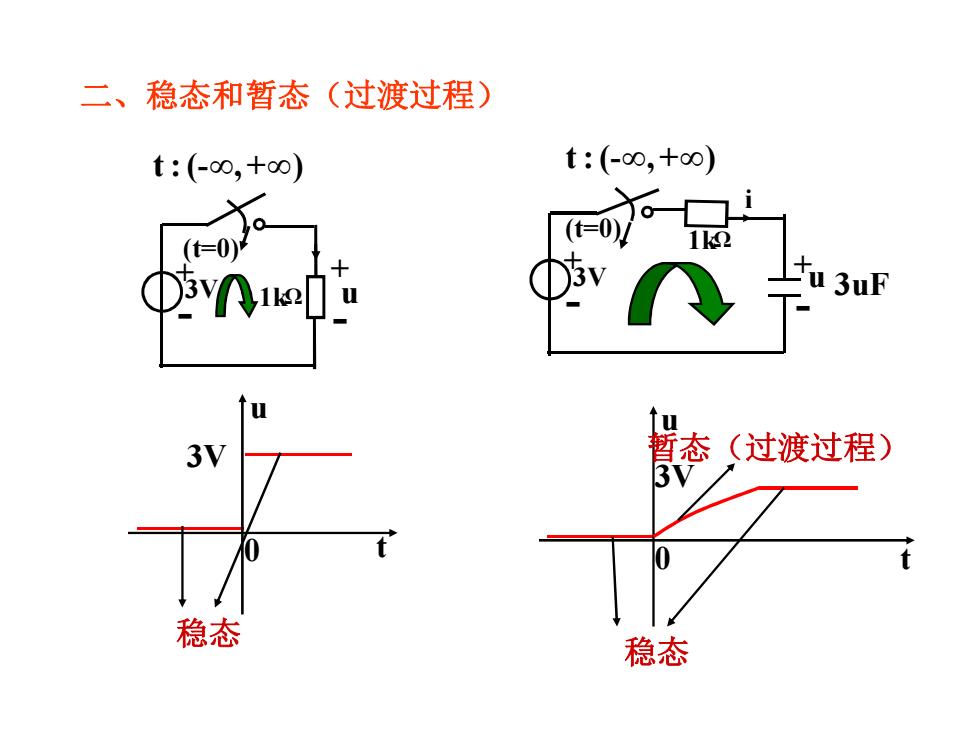
二、稳态和暂态(过渡过程) t:(-o0,+0) t:(-c0,+co) (t=0)/ 12 u 3uF 3V 暂态 (过渡过程) 3 稳态 稳态
Ҽǃっᘱ઼Ჲᘱ˄䗷䗷〻˅ 0 t u っᘱ 3V 0 t u 3V っᘱ Ჲᘱ˄䗷䗷〻˅ 3V+ - 1k (t=0) ȍ t : (- , + ) f f u + - t : (- , + ) f f 3V+ - 1k i (t=0) ȍ 3uF + - u
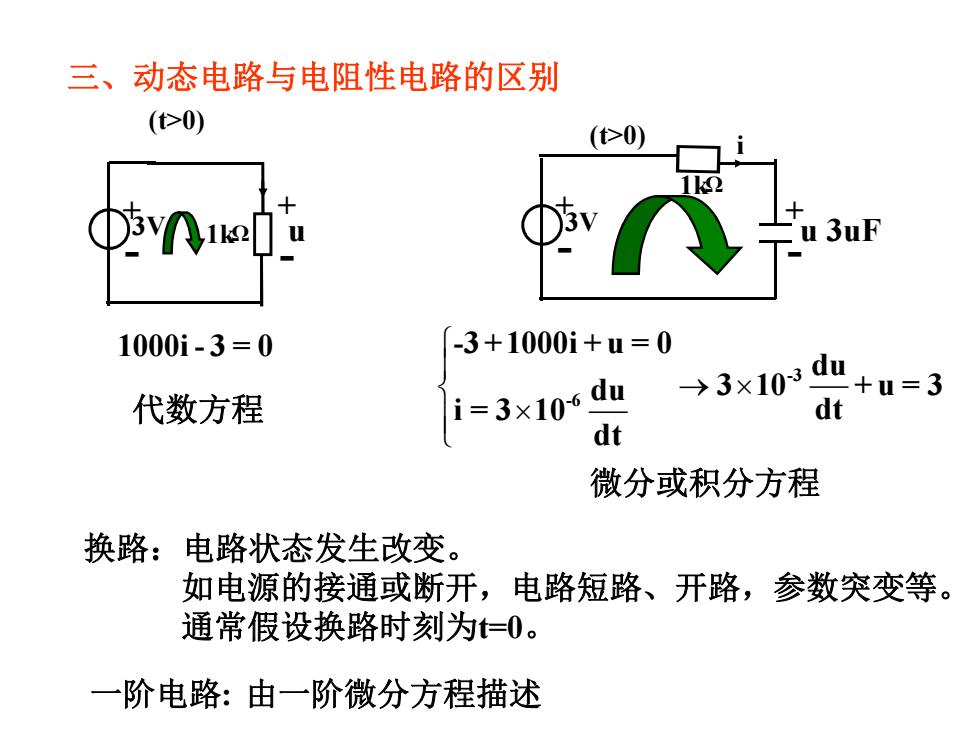
三、动态电路与电阻性电路的区别 (>0) (t>0) ①iv个attu u3uF 1000i-3=0 -3+1000i+u=0 代数方程 i=3x10c du →3×103d +u=3 dt dt 微分或积分方程 换路:电路状态发生改变。 如电源的接通或断开,电路短路、开路,参数突变等。 通常假设换路时刻为t=0。 一阶电路:由一阶微分方程描述
йǃࣘᘱ⭥䐟о⭥䱫ᙗ⭥䐟Ⲵ४࡛ ԓᮠᯩ〻 ᗞ࠶ᡆ〟࠶ᯩ〻 а䱦⭥䐟: ⭡а䱦ᗞ࠶ᯩ〻᧿䘠 1000i - 3 = 0 ° ® o u u ° ¯ -3 -6 -3 +1000i + u = 0 du du 3 10 + u = 3 i = 3 10 dt dt 3V+ - 1k (t>0) ȍ u + - 3V+ - 1k i (t>0) ȍ 3uF + - u ᦒ䐟˖⭥䐟⣦ᘱਁ⭏᭩ਈDŽ ྲ⭥ⓀⲴ᧕䙊ᡆᯝᔰˈ⭥䐟⸝䐟ǃᔰ䐟ˈ৲ᮠケਈㅹDŽ 䙊ᑨۇٴ䇮ᦒ䐟ᰦѪt=0DŽ
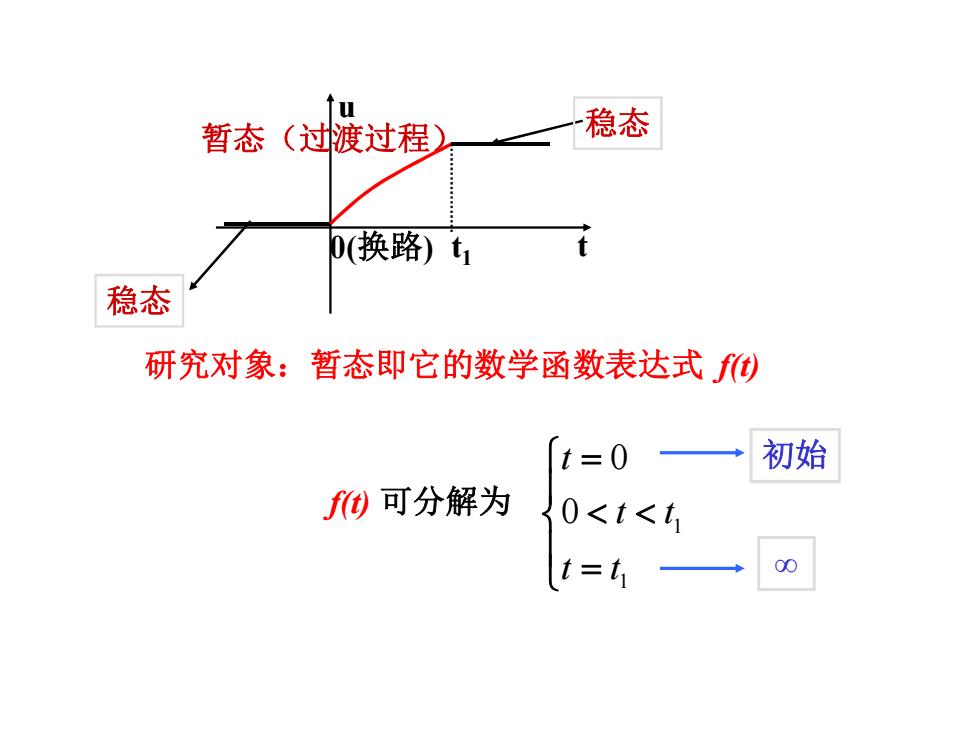
暂态(过渡过程) 稳态 0(换路)t 稳态 研究对象:暂态即它的数学函数表达式) t=0 初始 f)可分解为 0<t<t1 t=t 00
⹄ウሩ䊑˖ᲲᘱণᆳⲴᮠᆖ࠭ᮠ㺘䗮ᔿ f(t) 1 1 0 0 t t t t t ° ® ° ¯ f(t) ਟ࠶䀓Ѫ 0(ᦒ䐟) t u っᘱ Ჲᘱ˄䗷䗷〻˅ t1 っᘱ ࡍ