
电流1,从功率平衡角度看,二次绕组有电流,意味着有功率输出,一次绕组应增大相应 的电流,增加输入功率,才能达到功率平衡 变压器负载运行时,由于1《,可以认为一、二次电流关系为 i- 对降压变压器,12>I:对升压变压器12<1.无论是升压或降压变压器,额定负载 时,一、二次电流同时都为额定值(见变压器的铭牌). 2.负戴时二次电压、电流的关系 二次绕组磁动势户。=N:还要产生只环链二次绕组本身,而不环链一次绕组的称 为二次绕组稀磁通,其低值用中表示.它走的磁路如图2-9所示.与一次绕组漏磁通$, 对照,虽然各自的路径不同,但磁路材料性质都基本一样,包括了一段铁磁材料和一段 非铁磁材料.因此,本走的磁路也可以近似认为是线性磁路,且漏磁导A很小.在 次绕组中感应的电动势为E.中与它:的正方向如图 2-1所示,二者符合右手螺旋关系. 铁心 参照式(2-9),得 -学。 =-j4.44N,a 还可以写成 En=-joLnI: =-Xi: (2-26) NΦ 式中,La= 称为二次绕组漏自感; 图2-9一,二次绕组的清苦通 X,=L称为二次绕组漏电抗.当频率仙恒定时,为一常数.X:的数值也很小。 二次绕组的电阻用R,表示,当i2流过R,时,产生的压降为i,R根据电路的基尔 猫夫定律,参见图21中二次回路各电量的规定正方向,列出二次回路电压方程为 02=E2+龙e-iR2 =E2-i(R+X2)=E:-1Z (2-27) 式中,Z:=R十X:称为二次绕组漏阻抗 玉,变压器的基本方程式 综合前面推导各电磁量的关系,即式(2-22)、(2-27)、(2-14)、(2-25)、(218)和 (2-20),得变压器稳态运行时基本方程式, ·21·
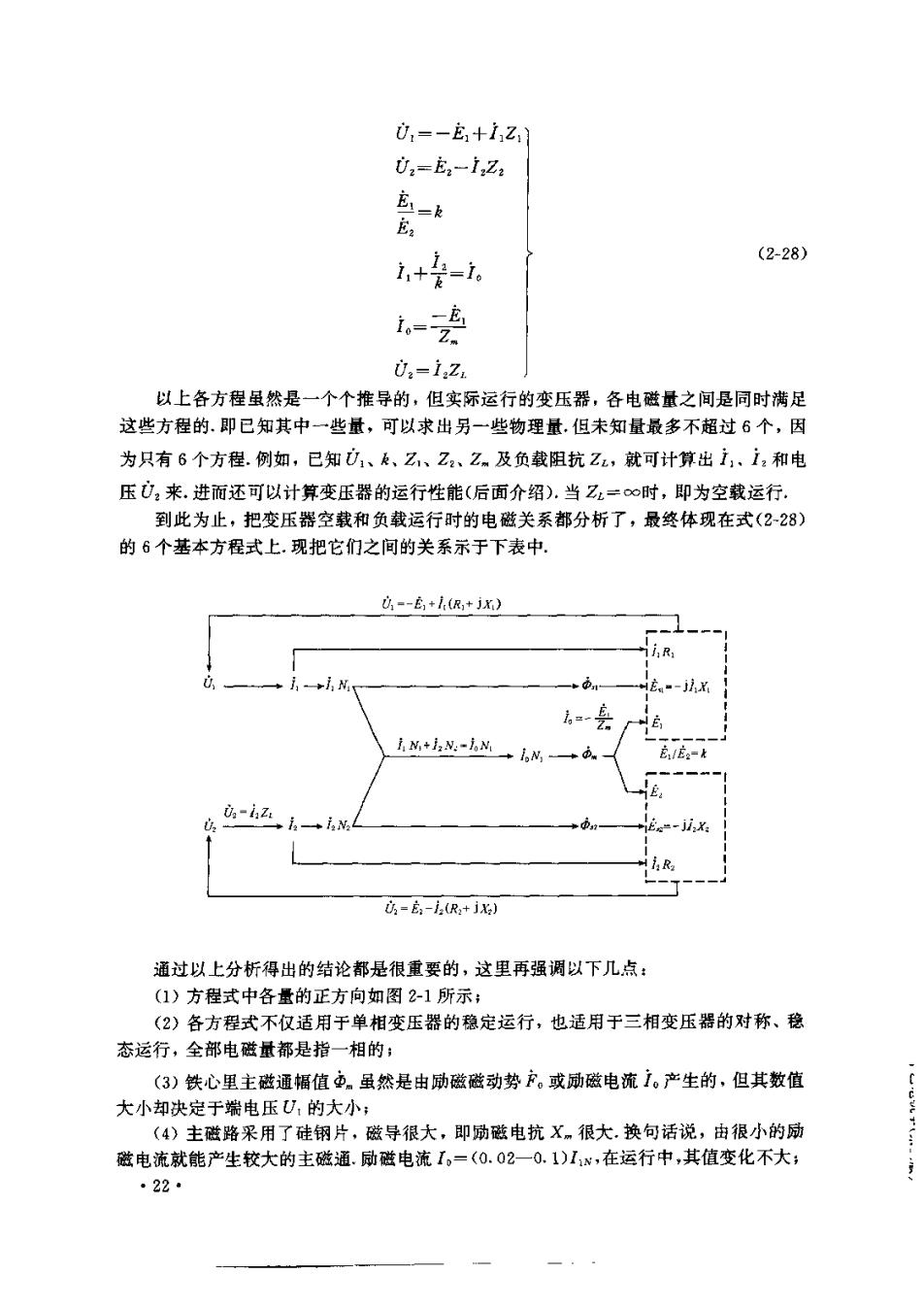
0,=-E1+1Z 02=E2一1Z2 (2-28) i+是=1。 -去 02=iZ 以上各方程虽然是一个个推导的,但实际运行的变压器,各电磁量之间是同时满足 这些方程的.即已知其中一些量,可以求出另一些物理量.但未知量最多不超过6个,因 为只有6个方程.例如,已知0、Z、Z、Z.及负载阻抗Z,就可计算出i、,和电 压0,来.进而还可以计算变压器的运行性能(后面介绍).当Z一∞时,即为空载运行 到此为止,把变压器空载和负载运行时的电磁关系都分析了,最终体现在式(2-28) 的6个基本方程式上.现把它们之间的关系示于下表中. a-高++j) R E。"-j N.+izN:-ioN ji.X: U=E:-l(R2+jxs) 通过以上分析得出的结论都是很重要的,这里再强调以下几点: (1)方程式中各量的正方向如图21所示; (2)各方程式不仅适用于单相变压器的稳定运行,也适用于三相变压器的对称、稳 态运行,全部电磁量都是指一相的: (3)铁心里主磁通幅值。虽然是由励磁磁动势。或动磁电流1。产生的,但其数值 大小却决定于端电压U,的大小; (4)主磁路采用了硅钢片,磁导很大,即励磁电抗X。很大.换句话说,由很小的励 磁电流就能产生较大的主磁通.励磁电流,=(0.02一0.1)1,在运行中,其值变化不大; ·22·

(5)漏磁路主要由非铁磁材料构成,对应的漏电抗X、X:数值很小: (6)当变压器一次绕组接额定电压心w,负载运行时,由于主磁通中。、一次和二次 电动势E:、E:数值变化不大,再加上一、二次稀阻抗Z、Z,数值很小,二次电压U:大 小变化也不大,属恒压源性质.当减小负载阻抗2红,则能增大二次电流12,而一次电流 i:也相应增大(反之亦然), (?)应掌握根据规定正方向判断变压器负载运行时功率(包括有功、无功)流动方向 及性质 4折合算法 从分析变压器电磁关系,得出了式(2-28)6个基本方程式,依此就可以分析其对称、 稳态运行性能.只要未知数不超过6个,解联立方程式,就能得到确定的解答.但是,当 变比较大时,一、二次电压、电流和漏阻抗等在数值相差很大,计算起来不方便,也不 精确,用同一比例尺画相盘图也很困难。通常采用折合算法克服这一困难。 变压器的一、二次绕组在电路上没有直接联系,仅有磁路的联系,从式(224)磁动势 平衡关系看出,二次绕组带负载时,二次绕组产生磁动势户2=,N,一次绕组磁动势中 同时增加一个负载分量(一F2)=(一1zNz)与二次绕组磁动势相平衡.这就是说,二次负 载电流:是通过它产生的磁动势户,与一次绕组联系的.可见,只要保持户,不变,就不 会影响一次的广,发生变化,为此,我们完全可以把实际二次绕组的匝数假想成为N,、电 流为:,令N,的大小和相位与原F:相同,即 IN:=I:N:=F 这样,一次虽不受任何影响,但磁动势平衡方程式可改写为 I:N+iN=ioN 消去N则为 1+i=io 上式中不再出现匝数N和N:了,磁动势平衡方程式成了很简单的电流平衡关系.!与 i:的关系为 =0=i: (229) 保持绕组磁动势值不变,而假想改变其匝数和电流的方法,称为折合算法.如果保 持二次绕组磁动势不变,而假想它的匝数与一次绕组匝数相同的折合算法,称为二次绕 组折合成一次绕组或简称为二次向一次折合.当然可以一次向二次折合,或者一次、二 次绕组匝数都折合到某一匝数N上 实际绕组的各个量称为实际值或称折合前的值,假想绕组的各个量称为折合值或折 合后的值.例如,二次绕组的实际值为心:、E,、1:以及Z:=R十X,其折合值用上角加 ”做标记,为、以及Z一R:十X.实际值与折合值或折合前的值与折合后的 值之间有一定的关系,称为换算关系.将二次绕组向一次绕组折合,其换算关系推导如下: ·23

电动势换算关亲 实际值 E:=-j4.44fN,西 折合值 E=-j4.44/N, 于是 -总点-kE (230) 阻抗换算关亲 实际值 2=龙2-i,2 Ea=0+1,Z=i(Z+Z2) 点-t2 折合值 +石贵-款喷 =k2(Z:+Z2) =kZ十k2 于是 Z=2或R=R,X=X Z=kZ2或R=kR2,X:=kX: (2-31) 上式说明,阻抗折合值为实际值的倍.由于电阻和电抗都同时差?倍,折合前后 的阻抗角不会改变. 端电压换算关 实际值 0=E2-1Z2 折合值 =龙2-1:z =kk:-iak'Za =k(E-iZ2)=k0: (2-32) 以上换算关系表明,电压、电流、电动势折合时,只变大小,相位不变;各参数折合 时,只变大小,阻抗角不变. 折合算法不改变变压器的功率传递关系.证明如下.先看一次侧折合算法的依据是 折合前后维持磁动势户,不变,一次侧各量值都不变,当然不会改变一次侧的功率关系。 ·24

二次侧的功率关系计算如下 二次侧铜损耗,用pc表示 pca=mrR=m京kR2 =m经R2 式中,m为相数。m=1是单相变压器,m=3是三相变压器.上式说明,折合前后二次绕 组铜损耗大小一样。 二次侧的有功功率P, P:-mUiTicose=mkU:cos =mU,Icosa 式中,c0s%是二次侧负载的功率因数.%是负载阻抗Z:有阻抗角,折合前后不变,因 此,cos%也不应变化. 上式说明,折合前后二次侧有功功率不改变 二次侧的无功功率Q Q:-mU:Iising=mkU:Ising =mU,I:sing 上式说明,折合前后无功功率也不变化 以上分析说明,折合算法仅仅作为一个方法来使用,不改变变压器运行的物理本 质,例如,并不改变电源向变压器输入功率,也不改变它向负载输出功率,更不改变它自 身的损耗。 当二次向一次折合时,一次侧各量为实际值,二次侧变为带”的量,如果要找二次 回路各量的实际值,再按上述公式把折合值换算为实际值, 5.等效电路 采用折合算法后,变压器一次侧量为实际值、二次侧量为折合值,基本方程式就成为 01=-E+12】 0=E-1:24 E=: 1+i=1。 (2-33) 1-多 U-lz 根据以上6个方程式,找出变压器的等效电路如图2-10所示.图中二次绕组两端接 着的负载阻抗的折合值为Z,若只看变压器本身的等效电路,其形状像字母“T”,故称 为T型等效电路。 采用折合算法后,使原本无电路联系的双绕组变压器,其一、二次电动势相等 ·25◆