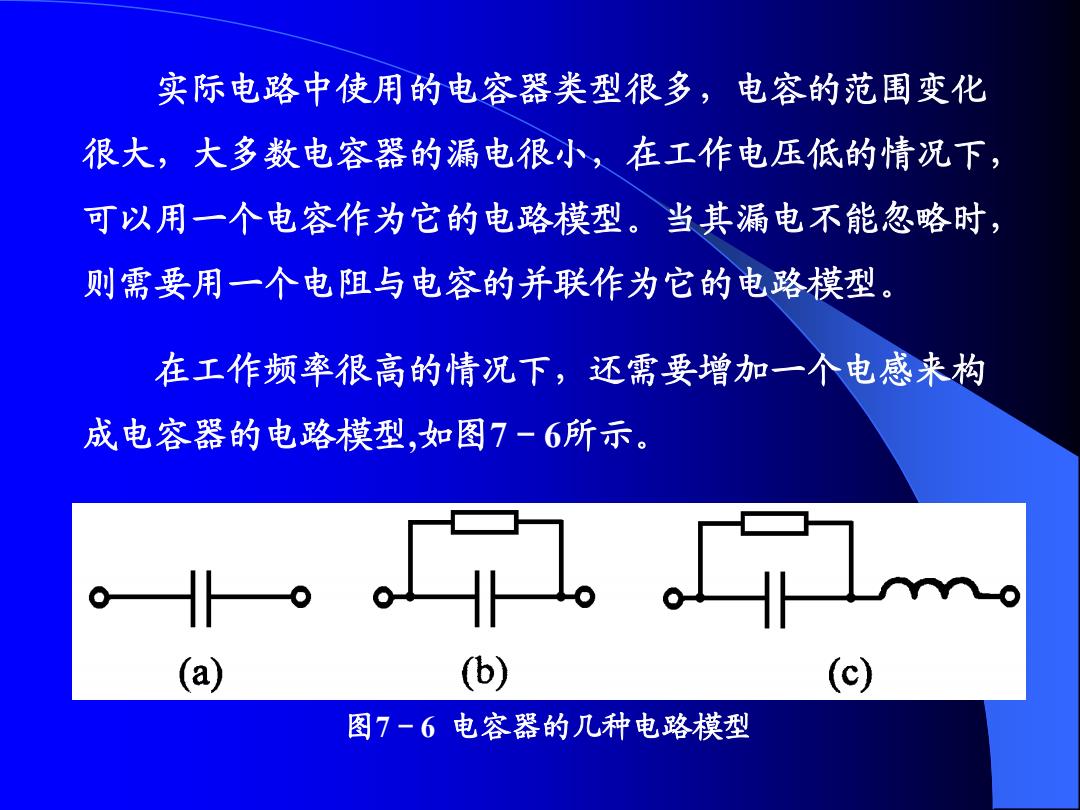
实际电路中使用的电容器类型很多,电容的范围变化 很大,大多数电容器的漏电很小,在工作电压低的情况下, 可以用一个电容作为它的电路模型。当其漏电不能忽略时, 则需要用一个电阻与电容的并联作为它的电路模型。 在工作频率很高的情况下,还需要增加一个电感来构 成电容器的电路模型,如图7-6所示。 a (b) 图7一6电容器的几种电路模型
实际电路中使用的电容器类型很多,电容的范围变化 很大,大多数电容器的漏电很小,在工作电压低的情况下, 可以用一个电容作为它的电路模型。当其漏电不能忽略时, 则需要用一个电阻与电容的并联作为它的电路模型。 在工作频率很高的情况下,还需要增加一个电感来构 成电容器的电路模型,如图7-6所示。 图7-6 电容器的几种电路模型

二、电容元件的电压电流关系 对于线性时不变电容元件来说,在采用电压电流关联 参考方向的情况下,可以得到以下关系式 du i(t)= dq d(Cu)=C (7-12) dt dt dt 此式表明电容中的电流与其电压对时间的变化率成正 比,它与电阻元件的电压电流之间存在确定的约束关系不 同,电容电流与此时刻电压的数值之间并没有确定的约束 关系。 在直流电源激励的电路模型中,当各电压电流均不随 时间变化的情况下,电容元件相当于一个开路(=0)
二、电容元件的电压电流关系 对于线性时不变电容元件来说,在采用电压电流关联 参考方向的情况下,可以得到以下关系式 (7 12) d d d d( ) d d ( ) t u C t Cu t q i t 此式表明电容中的电流与其电压对时间的变化率成正 比,它与电阻元件的电压电流之间存在确定的约束关系不 同,电容电流与此时刻电压的数值之间并没有确定的约束 关系。 在直流电源激励的电路模型中,当各电压电流均不随 时间变化的情况下,电容元件相当于一个开路(i=0)
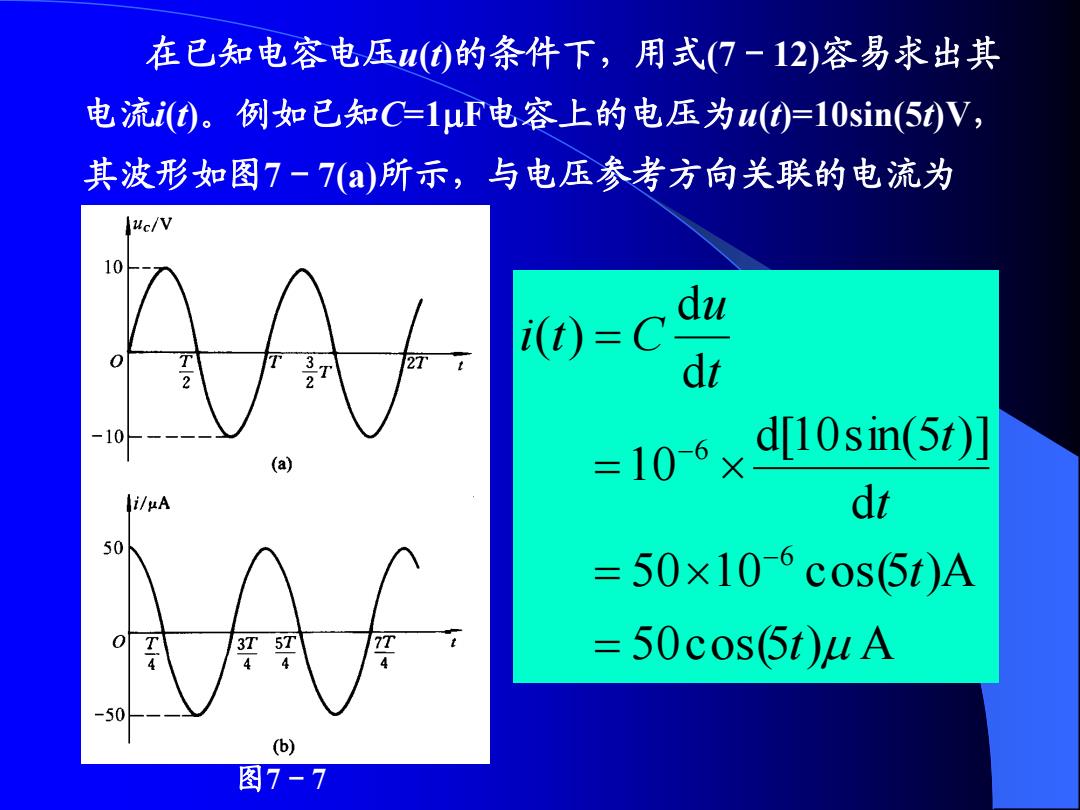
在已知电容电压()的条件下,用式(7-12)容易求出其 电流i(t)。例如已知C=1uF电容上的电压为u(t)=10sin(5)V, 其波形如图7-7(a)所示,与电压参考方向关联的电流为 uc/V 10 du i(t)=C 3T dt 10 =106× d[10sin(5t)] (a) i/uA dt 50 =50×106c0s5t)A 军 =50cos(5t)uA 50 (b) 图7-7
在已知电容电压u(t)的条件下,用式(7-12)容易求出其 电流i(t)。例如已知C=1F电容上的电压为u(t)=10sin(5t)V, 其波形如图7-7(a)所示,与电压参考方向关联的电流为 50cos(5 ) A 50 10 cos(5 )A d d[10sin(5 ) ] 10 d d ( ) 6 6 t t t t t u i t C 图7-7
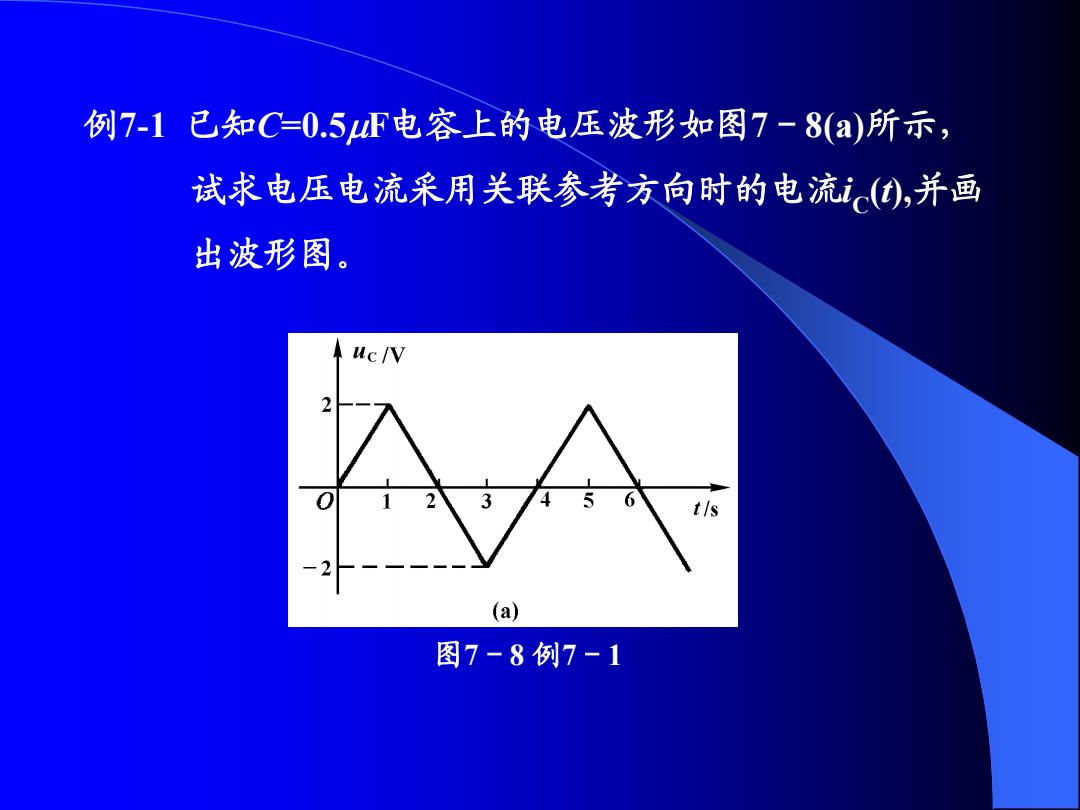
例7-1已知C=0.5F电容上的电压波形如图7-8(a)所示, 试求电压电流采用关联参考方向时的电流(①),并画 出波形图。 uc/V t/s (a) 图7-8例7-1
例7-1 已知C=0.5F电容上的电压波形如图7-8(a)所示, 试求电压电流采用关联参考方向时的电流iC (t),并画 出波形图。 图7-8 例7-1

解:根据图7-8(a波形的具体情况,按照时间分段来进行 计算 1.当0≤1s时,4c()=2t,根据式7-12可以得到 (t)= de=0.5x10-6d20-1x10A=lA d dt 2.当1s≤3s时,4c()=4-2t,根据式7-12可以得到 e0=cdk=0.5x106d4-20-1x10A=-1A dt dt
1 10 A = 1 A d d(2 ) 0.5 10 d d ( ) C 6 6 C t t t u i t C 2.当1st3s时,uC (t)=4-2t,根据式7-12可以得到 1 10 A 1 A d d(4 2 ) 0.5 10 d d ( ) C 6 6 C t t t u i t C 1.当0t1s 时,uC (t)=2t,根据式7-12可以得到 解:根据图7-8(a)波形的具体情况,按照时间分段来进行 计算