四、样本回归函数(SRF) 样本回归线: 对于X的一定值,取得Y的样本观测值,可计算其条 件均值,样本观测值条件均值的轨迹称为样本回归线。 样本回归函数: 如果把应变量Y的样本条件均值表示为解释变量的某 种函数,这个函数称为样本回归函数(SRF)
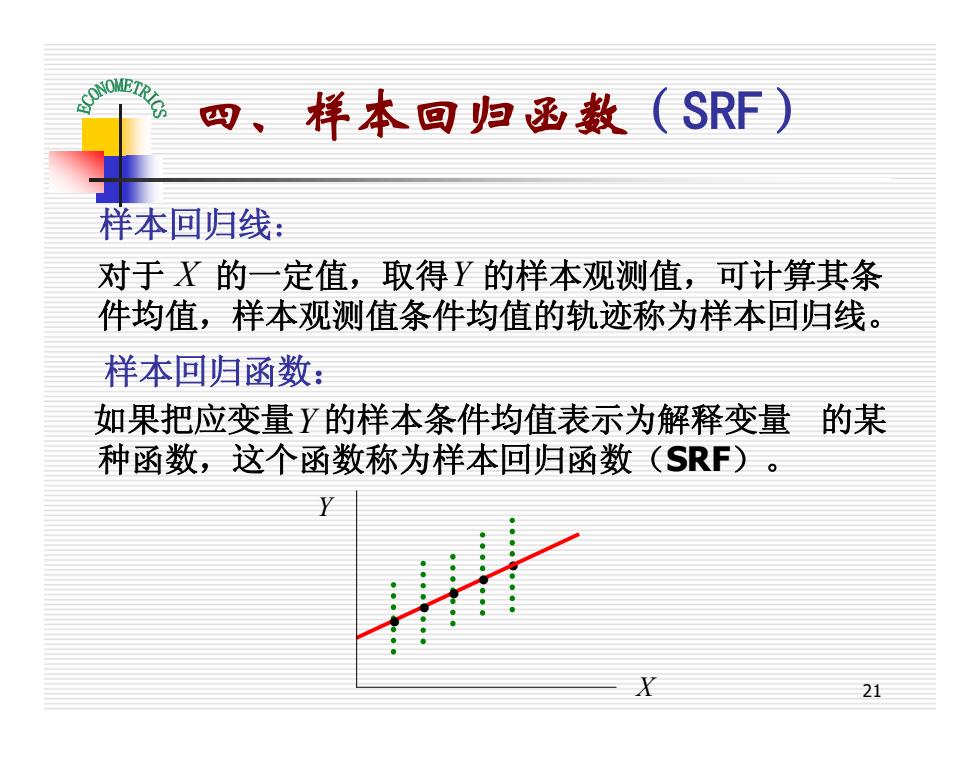
21 四、样本回归函数(SRF) · 样本回归线: 对于 的一定值,取得 的样本观测值,可计算其条 件均值,样本观测值条件均值的轨迹称为样本回归线。 样本回归函数: 如果把应变量 的样本条件均值表示为解释变量 的某 种函数,这个函数称为样本回归函数(SRF)。 · · · · X Y Y Y X

SRF的特点 ● 每次抽样都能获得一个样本,就可以拟合一条 样本回归线,所以样本回归线随抽样波动而变 化,可以有许多条(SRF不唯一)。 SRF1 SRF2 22
22 SRF 的特点 ●每次抽样都能获得一个样本,就可以拟合一条 样本回 归线,所以样本回归线随抽样波动而变 化,可以有许多条(SRF不唯一)。 SRF2 SRF1 Y X

样本回归函数的函数形式应与设定的总体回归 函数的函数形式一致。 ●样本回归线还不是总体回归线,至多只是未知 总体回归线的近似表现。 23
23 ●样本回归函数的函数形式应与设定的总体回归 函数的函数形式一致。 ●样本回归线还不是总体回归线,至多只是未知 总体回归线的近似表现

样本回归函数的表现形式 样本回归函数如果为线性函数,可表示为 V=B+BX 其中:是与X,相对应的Y的样本条件均值 B,和B2分别是样本回归函数的参数 应变量Y的实际观测值Y不完全等于样本条件 均值,二者之差用e,表示,e,称为剩余项或残差项: e=Y,- 或者 Y=B+B2X,+e 24
24 1 2 ˆ ˆ ˆ Y X i i = + b b 样本回归函数如果为线性函数,可表示为 其中: 是与 相对应的 的样本条件均值 和 分别是样本回归函数的参数 应变量 的实际观测值 不完全等于样本条件 均值,二者之差用 表示, 称为剩余项或残差项: 或者 样本回归函数的表现形式 1 2 ˆ ˆ Yi = b b + + X e i i ˆ i i i e = - Y Y i e Xi Yi ˆ Yi 1 ˆ b 2 ˆ b i e Y Y

对样本回归的理解 Y=B+BX +e 如果能够获得B,和B,的数值,显然: 。B和B2是对总体回归函数参数阝,和阝的估计 ●,是对总体条件期望EYX)的估计 ●e,在概念上类似总体回归函数中的4,可 视为对u,的估计。 25
25 对样本回归的理解 如果能够获得 和 的数值,显然: ● 和 是对总体回归函数参数 和 的估计 ● 是对总体条件期望 的估计 ● 在概念上类似总体回归函数中的 ,可 视为对 的估计。 i e ˆYi i u E( ) Y Xi 1 2 ˆ ˆ Yi = b b + + X e i i 1 ˆb 2 ˆb 2 ˆ 1 b ˆb b1 b2 i u