
2.总体回归函数的表现形式 (1)条件均值表现形式 假如Y的条件均值E(YX)是解 释变量X的线性函数,可表示为: E(Y X E(YX)=∫(X)=阝+阝2X (2)个别值表现形式 对于一定的X,Y的各个别值Y分布 在E(Yx,)的周围,若令各个Y与条件 均值E(YX,)的偏差为u,显然4是随机变量,则有 4,=y,-E(X,)=Y,-阝,-阝2X 或 Y=B +B,X+u 16
16 · · ui Xi X Y ( ) E Y Xi Yi (1)条件均值表现形式 假如 的条件均值 是解 释变量 的线性函数,可表示为: (2)个别值表现形式 对于一定的 , 的各个别值 分布 在 的周围,若令各个 与条件 均值 的偏差为 , 显然 是随机变量,则有 或 2.总体回归函数的表现形式 Xi E( ) Y Xi E 1 2 ( ) ( ) Yi Xi i i = f X X = + b b Yi E( ) Y Xi Yi E( ) Y Xi i u i u E 1 2 ( ) i i i i i i u = Y - Y X = Y X - - b b Yi = b b 1 2 + + X u i i Y Y X

3.如何理解总体回归函数 实际的经济研究中总体回归函数通常是未知的, 只能根据经济理论和实践经验去设定。“计量” 的目的就是寻求PRF。 。总体回归函数中Y与X的关系可是线性的,也可 是非线性的。 对线性回归模型的“线性”有两种解释 就变量而言是线性的 Y的条件均值是X的线性函数 就参数而言是线性的 Y的条件均值是参数B的线性函数
17 ●实际的经济研究中总体回归函数通常是未知的, 只能根据经济理论和实践经验去设定。“计量” 的目的就是寻求PRF。 ●总体回归函数中 与 的关系可是线性的,也可 是非线性的。 对线性回归模型的“线性”有两种解释 就变量而言是线性的 —— 的条件均值是 的线性函数 就参数而言是线性的 —— 的条件均值是参数 的线性函数 3.如何理解总体回归函数 Y X Y Y X b

“线性”的判断 E(Y X=B+B,X 变量、参数均为“线性” E(X)=β+阝2X号 参数“线性”,变量非线性” EYX)=β+VB,X 变量“线性”,参数"非线性 计量经济学中 线性回归模型主要指就参数而言是“线性”,因 为只要对参数而言是线性的,都可以用类似的方法估计 其参数。 18
18 变量、参数均为“线性” 参数“线性” ,变量”非线性” 变量“线性” ,参数”非线性” 计量经济学中: 线性回归模型主要指就参数而言是“线性” ,因 为只要对参数而言是线性的,都可以用类似的方法估计 其参数。 E 1 2 ( ) Yi X X i i = + b b 2 E 1 2 ( ) Yi X X i i = + b b E 1 2 ( ) Yi X X i i = + b b “线性”的判断
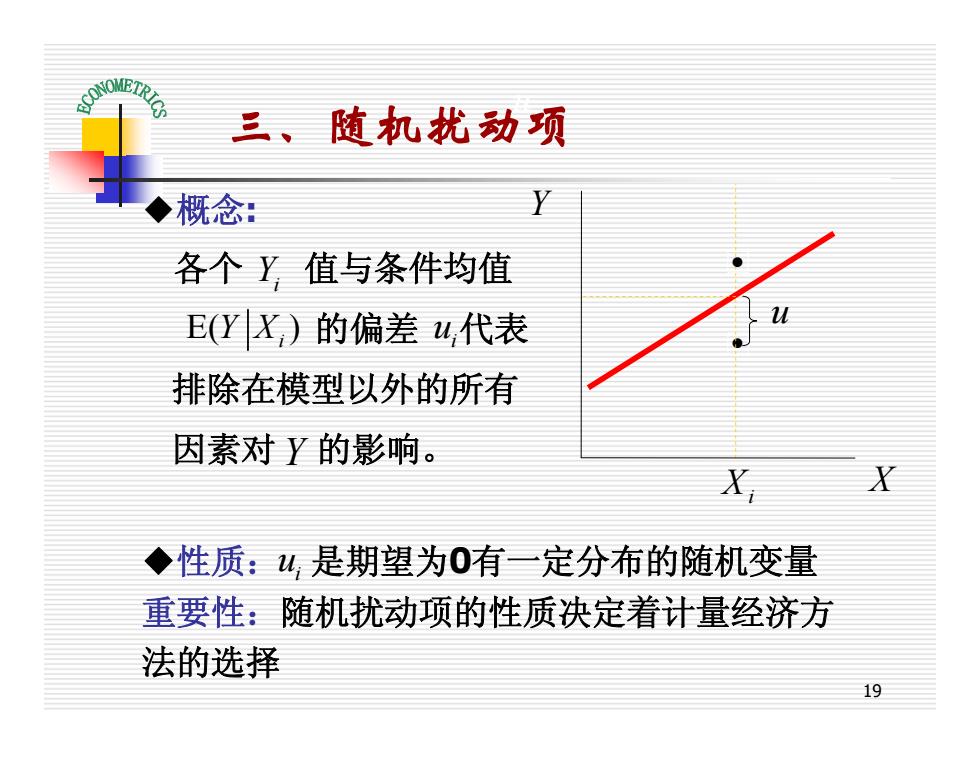
三、随机扰动项 概念: 各个Y值与条件均值 E(YX)的偏差u代表 排除在模型以外的所有 因素对Y的影响。 XX ◆性质:u是期望为0有一定分布的随机变量 重要性:随机扰动项的性质决定着计量经济方 法的选择 19
19 三、随机扰动项 ◆概念: 各个 值与条件均值 的偏差 代表 排除在模型以外的所有 因素对 的影响。 ◆性质: 是期望为0有一定分布的随机变量 重要性:随机扰动项的性质决定着计量经济方 法的选择 · · u Yi i u Y X Xi u E( ) Y Xi Y i u

引入随机扰动项的原因 未知影响因素的代表 无法取得数据的已知影响因素的代表 众多细小影响因素的综合代表 模型的设定误差 变量的观测误差 变量内在随机性 20
20 ● 未知影响因素的代表 ● 无法取得数据的已知影响因素的代表 ● 众多细小影响因素的综合代表 ● 模型的设定误差 ● 变量的观测误差 ● 变量内在随机性 引入随机扰动项的原因