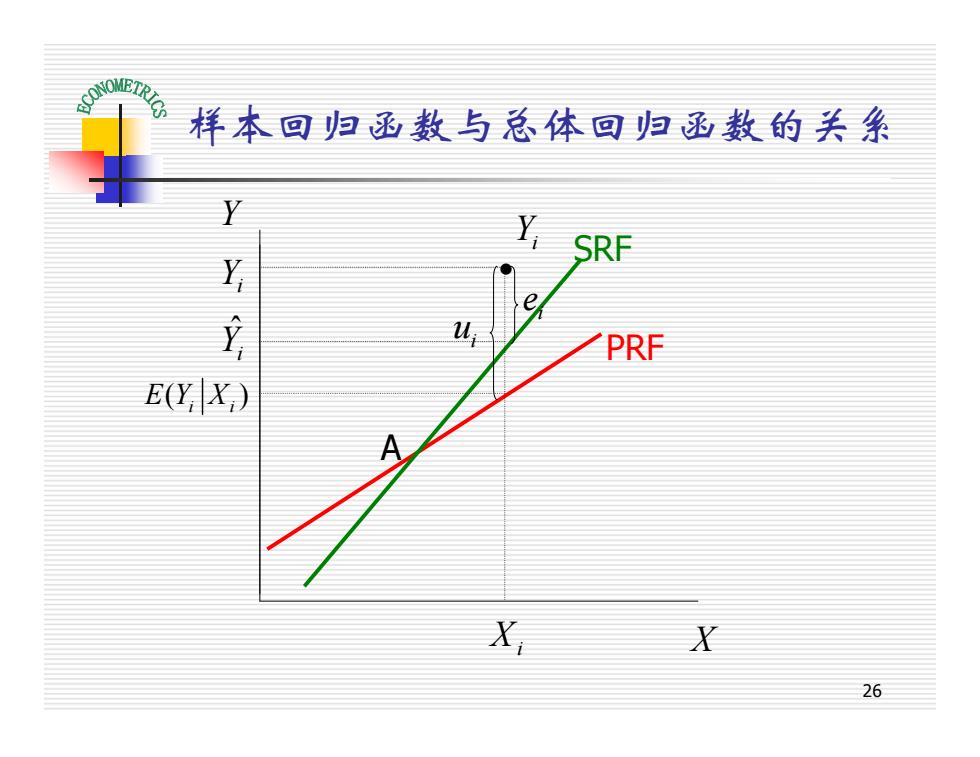
样本回归函数与总体回归函数的关系 SRF 1 PRF EY X) X X 26
26 样本回归函数与总体回归函数的关系 SRF PRF A · i u i e ˆ Yi ( ) E Y Xi i Yi Y Xi X Yi

回归分析的目的 用样本回归函数SRF去估计总体回归函数PRF。 由于样本对总体总是存在代表性误差,SRF总会过 高或过低估计PRF。 要解决的问题: 寻求一种规则和方法,使得到的SRF的参数阝和阝, 尽可能“接近”总体回归函数中的参数阝,和阝2。 这样的“规则和方法”有多种,最常用的是最小二乘 法 27
27 1 ˆ b 回归分析的目的 用样本回归函数SRF去估计总体回归函数PRF。 由于样本对总体总是存在代表性误差,SRF 总会过 高或过低估计PRF。 要解决的问题: 寻求一种规则和方法,使得到的SRF的参数 和 尽可能“接近”总体回归函数中的参数 和 。 这样的“规则和方法”有多种,最常用的是最小二乘 法 2 ˆ b b1 b2

第二节 简单线性回归模型的最小二乘估计 本节基本内容: ● 简单线性回归的基本假定 普通最小二乘法 OLS回归线的性质 参数估计式的统计性质 28
28 第二节 简单线性回归模型的最小二乘估计 本节基本内容: ● 简单线性回归的基本假定 ● 普通最小二乘法 ● OLS回归线的性质 ● 参数估计式的统计性质

一、简单线性回归的基本假定 1.为什么要作基本假定? ●模型中有随机扰动,估计的参数是随机变量, 只有对随机扰动的分布作出假定,才能确定 所估计参数的分布性质,也才可能进行假设 检验和区间估计 ●只有具备一定的假定条件,所作出的估计才 具有较好的统计性质。 29
29 一、简单线性回归的基本假定 1. 为什么要作基本假定? ●模型中有随机扰动,估计的参数是随机变量, 只有对随机扰动的分布作出假定,才能确定 所估计参数的分布性质,也才可能进行假设 检验和区间估计 ●只有具备一定的假定条件,所作出的估计才 具有较好的统计性质

2、基本假定的内容 (1)对模型和变量的假定 如Y=阝+B2X,+% 假定解释变量X是非随机的,或者虽然是随机的,但与扰动 项2儿是不相关的 假定解释变量X在重复抽样中为固定值 假定变量和模型无设定误差 30
30 (1)对模型和变量的假定 如 假定解释变量 是非随机的,或者虽然是随机的,但与扰动 项 是不相关的 假定解释变量 在重复抽样中为固定值 假定变量和模型无设定误差 2、基本假定的内容 Yi = b b 1 2 + + X u i i X u X