
可见,H(Z)与采样周期T有 关,T越小,H(Z)的相对增益越大,这 是不希望的。为此,实际应用脉冲响应不 变法时稍作一点修改,即求出H(Z)后, 再乘以因子T,使H(Z)只与 f1f有关, 即只与fc和f的相对值 Qc 有关, 而与采样频率f、无直接关系。 例如,f,=4KE,f=1KE与f=40KE,f.=10KTE 的数字滤波器具有相同的传递函数,这一 结论适合于所有的数字滤波器设计。最后 得: 1.571 -1.571+0.5541z- H(Z)= 1-0.2079z11-0.1905z1+0.2079z2
可见,H(Z)与采样周期T有 关,T越小,H(Z)的相对增益越大,这 是不希望的。为此,实际应用脉冲响应不 变法时稍作一点修改,即求出H(Z)后, 再乘以因子T,使H(Z)只与 有关, 即只与fc和fs的相对值 有关, 而与采样频率fs无直接关系。 例如, 与 的数字滤波器具有相同的传递函数,这一 结论适合于所有的数字滤波器设计。最后 得: c s f / f 1 2 1 1 1 0.1905 0.2079 1.571 0.5541 1 0.2079 1.571 ( ) − − − − − + − + + − = z z z z H Z C f KHz f KHz f s = 4KHz, f c =1KHz s = 40 , c =10

b.双线性变换法 (一)首先确定数字域临界频率0。=2T=0.5m (二)根据频率的非线性关系,确定预畸的模 (三)以s/①C代入归一化的三阶巴特沃模拟器传递函 数 1 H(s)= 1+2(s/2)+2(s/2)2+(s/2)月 并将2=2/T代入上式。 (四)将双线性变换关系代入,求H(Z)
b. 双线性变换法 (一)首先确定数字域临界频率 c = 2f c T = 0.5 T t g T c c 2 2 2 = = 2 3 1 2( / ) 2( / ) ( / ) 1 ( ) c c c a s s s H s + + + = (二)根据频率的非线性关系,确定预畸的模 拟滤波器临界频率 (三 ) 以 代入归一化的三阶巴特沃模拟器传递函 数 并将 代入上式。 (四)将双线性变换关系代入,求H(Z)。 s/c c = 2/T

HZ=HS) 21-2 1+z_10+z 3+z1+z+1-z)23+z
3 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 2 1 ( ) ( ) 1 1 + − + + − + + − + = = − − − − − − + − = − − z z z z z z H Z H s z z T s a ( ) ( )( ) ( ) 2 3 1 2 1 1 3 1 3 1 2 1 3 1 1 1 − − − − − − + + = + + + − + = z z z z z z
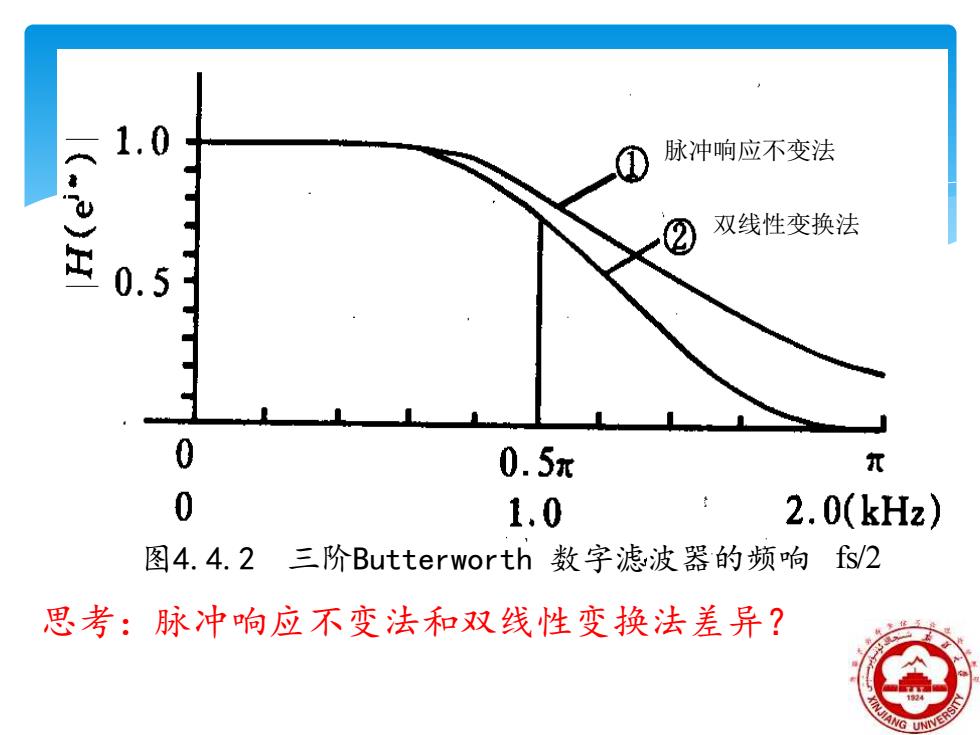
1.0 脉冲响应不变法 (·e仕 双线性变换法 0.5 0 0.5π T 0 1.0 2.0(kHz) 图4.4.2三阶Butterworth数字滤波器的频响fs/2 思考:脉冲响应不变法和双线性变换法差异?
脉冲响应不变法 双线性变换法 图4.4.2 三阶Butterworth 数字滤波器的频响 fs/2 思考:脉冲响应不变法和双线性变换法差异?
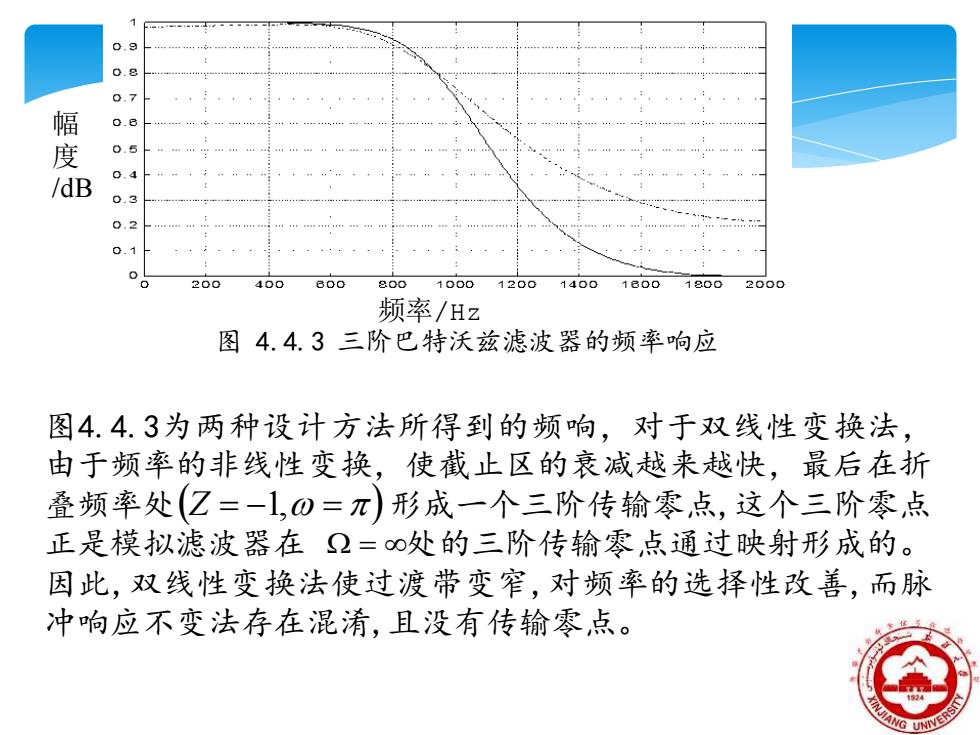
0.9 0.8 0.7 幅 0.8 度 0.5n.g.4. 0.4 /dB 0.3 0.2 0.1 200 400 600 800 1000 1200 14001800 18002000 频率/Hz 图4.4.3三阶巴特沃兹滤波器的频率响应 图4.4.3为两种设计方法所得到的频响,对于双线性变换法, 由于频率的非线性变换,使截止区的衰减越来越快,最后在折 叠频率处(Z=-1,0=π)形成一个三阶传输零点,这个三阶零点 正是模拟滤波器在Ω=∞处的三阶传输零,点通过映射形成的。 因此,双线性变换法使过渡带变窄,对频率的选择性改善,而脉 冲响应不变法存在混淆,且没有传输零点
频率/Hz 图 4.4.3 三阶巴特沃兹滤波器的频率响应 幅 度 /dB 图4.4.3为两种设计方法所得到的频响,对于双线性变换法, 由于频率的非线性变换,使截止区的衰减越来越快,最后在折 叠频率处 形成一个三阶传输零点,这个三阶零点 正是模拟滤波器在 处的三阶传输零点通过映射形成的。 因此,双线性变换法使过渡带变窄,对频率的选择性改善,而脉 冲响应不变法存在混淆,且没有传输零点。 (Z = −1, = ) =