
二.高通变换 设计高通、带通、带阻等数字滤波器时,有两种方法: ①先设计一个相应的高通、带通或带阻模拟滤波器,然后通 过脉冲响应不变法或双线性变换法转换为数字滤波器。 模拟原型→ 模拟高通、带通、带阻→数字高通、带通、带阻 设计方法同上面讨论的低通滤波器的设计。, 即确定{Ok) 一转换为相应的 2} 高通、带通、带阻模拟滤波器的设计 Ha(s) H(Z) ②直接利用模拟滤波器的低通原型,通过一定的频率变 换关系,一步完成各种数字滤波器的设计。 频率变换 模拟原型 数字低通、高通、带通、带阻
二.高通变换 设计高通、带通、带阻等数字滤波器时,有两种方法: ① 先设计一个相应的高通、带通或带阻模拟滤波器,然后通 过脉冲响应不变法或双线性变换法转换为数字滤波器。 模拟原型 模拟高通、带通、带阻 数字高通、带通、带阻 设计方法同上面讨论的低通滤波器的设计。 即确定 转换为相应的 高通、带通、带阻 模拟滤波器的设计 Ha(s) H(Z) ② 直接利用模拟滤波器的低通原型,通过一定的频率变 换关系,一步完成各种数字滤波器的设计。 频率变换 模拟原型 数字低通、高通、带通、带阻 k k

这里只讨论第二种方法。因其简捷便利,所以 得到普遍采用。 变换方法的选用: 脉冲响应不变法:对于高通、带阻等都不能 直接采用,或只能在加了保护滤波器后才可使 用。因此,使用直接频率变换(第二种方法), 对脉冲响应不变法要有许多特殊的考虑,它一 般应用于第一种方法中。 双线性变换法:下面的讨论均用此方法,实 际使用中多数情况也是如此
这里只讨论第二种方法。因其简捷便利,所以 得到普遍采用。 变换方法的选用: 脉冲响应不变法:对于高通、带阻等都不能 直接采用,或只 能在加了保护滤波器后才可使 用。因此,使用直接频率变换(第二种方法), 对脉冲响应不变法要有许多特殊的考虑,它一 般应用于第一种方法中。 双线性变换法:下面的讨论均用此方法,实 际使用中多数情况也是如此

模拟低通与高通滤波器的关系 基于双线性变换 法的高通滤波器 设计: 在模拟滤波 器的高通设计中, 低通至高通的变 换就是S变量的倒 置,这一关系同 样可应用于双线 性变换,只要将 变换式中的$代之 Hn 以1/S,就可得到 数字高通滤波器 即 H(jn)=G(j) T1+z S 2 1-z 0 n no 图4.4.4 低通与高通滤波器的幅度特性
1 = 1 H j G j ( ) ( ) = = 模拟低通与高通滤波器的关系 图4.4.4 低通与高通滤波器的幅度特性 基于双线性变换 法的高通滤波器 设计: 在模拟滤波 器的高通设计中, 低通至高通的变 换就是S变量的倒 置,这一关系同 样可应用于双线 性变换,只要将 变换式中的S代之 以1/S,就可得到 数字高通滤波器. 即 1 1 1 1 2 − − − + = z T z s

由于倒数关系不改变模拟滤波器的稳定性, 因此,也不会影响双线变换后的稳定条件,而 且2轴仍映射在单位圆上,只是方向颠倒了。 即 Z=eo时,s= 2 1-e-jo T
由于倒数关系不改变模拟滤波器的稳定性, 因此,也不会影响双线变换后的稳定条件,而 且 j 轴仍映射在单位圆上,只是方向颠倒了。 = = − − + = = − − jctg j T e T e Z e s j j j 1 2 2 1 2 , 时 = − 2 2 ctg T 即
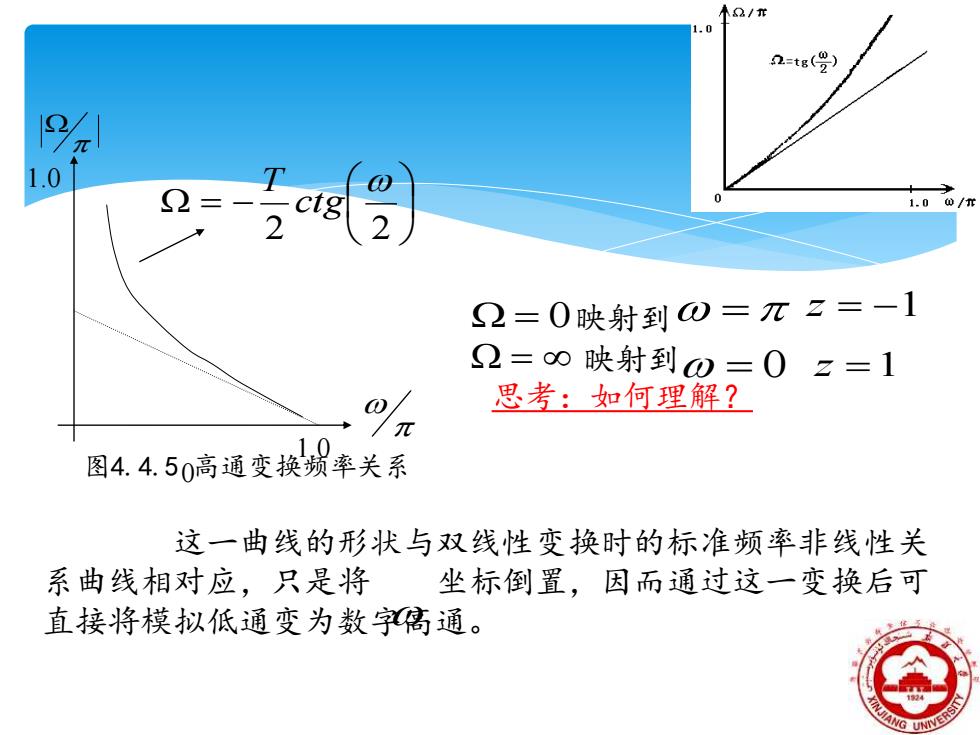
木2/r 2=tg() 1.0 1.00/r 2=0映射到ω=π2=-1 2=0 映射到0=02=1 思考:如何理解? /π 1.0 图4.4.50高通变换频率关系 这一曲线的形状与双线性变换时的标准频率非线性关 系曲线相对应,只是将 坐标倒置,因而通过这一变换后可 直接将模拟低通变为数字隔通。 UNIVERS
映射到 映射到 思考:如何理解? 图4.4.5 高通变换频率关系 这一曲线的形状与双线性变换时的标准频率非线性关 系曲线相对应,只是将 坐标倒置,因而通过这一变换后可 直接将模拟低通变为数字高通。 = − 2 2 ctg T = 0 = = z =1 z = −1 = 0 1.0 1.0 0