
4.数量积的坐标表示 设a=axi+a,j+a.k,b=bi+b,j+b.K,则 a.b=(axi+ay j+azK)(bsi+by j+b-k) ii=j=(=1,i了=jk=i=0 a·b=abx+aby+ab 两向量的夹角公式 当a,b为非零向量时,由于a.b=albcos0,得 cos0 a.b axbx +a,by +a_b aa++ab+b+h ogo⊙o☒
4. 数量积的坐标表示 设 则 = 0 x x y y z z =a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 ax + ay + az 2 2 2 bx + by + bz 由于 a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z (a i + a j + a k ) x y z (b i b j b k ) x + y + z i j = j k = k i a b a b 两向量的夹角公式 , 得 机动 目录 上页 下页 返回 结束

例2.已知三点M(1,1,1),A(2,2,1),B(2,1,2),求 ∠AMB A 解:MA=(1,1,0),MB=(1,0,1) B 则 coS∠AMB= MA.MB M MAMB 1+0+0 √/2/2 2 故 ∠AMB= 3 Q008
MA = ( ), MB = ( ) = B M 例2. 已知三点 M (1,1,1), A(2,2,1),B(2,1,2), AMB . A 解: 1, 1, 0 1, 0, 1 则 cos AMB = 1+0 +0 2 2 AMB = 求 MA MB MA MB 故 机动 目录 上页 下页 返回 结束

例3.设均匀流速为的流体流过一个面积为A的平 面域,且)与该平面域的单位垂直向量的夹角为0, 求单位时间内流过该平面域的流体的质量P(流体密度 为p). 解:P=PA coS0 为单位向量 -PAv.n 单位时间内流过的体积 4 cos0 Oa▣oo&
为 ) . 求单位时间内流过该平面域的流体的质量P (流体密度 例3. 设均匀流速为 的流体流过一个面积为 A 的平 面域 , 与该平面域的单位垂直向量 A 解: 单位时间内流过的体积 P = = A 且 的夹角为 v v v n 为单位向量 机动 目录 上页 下页 返回 结束
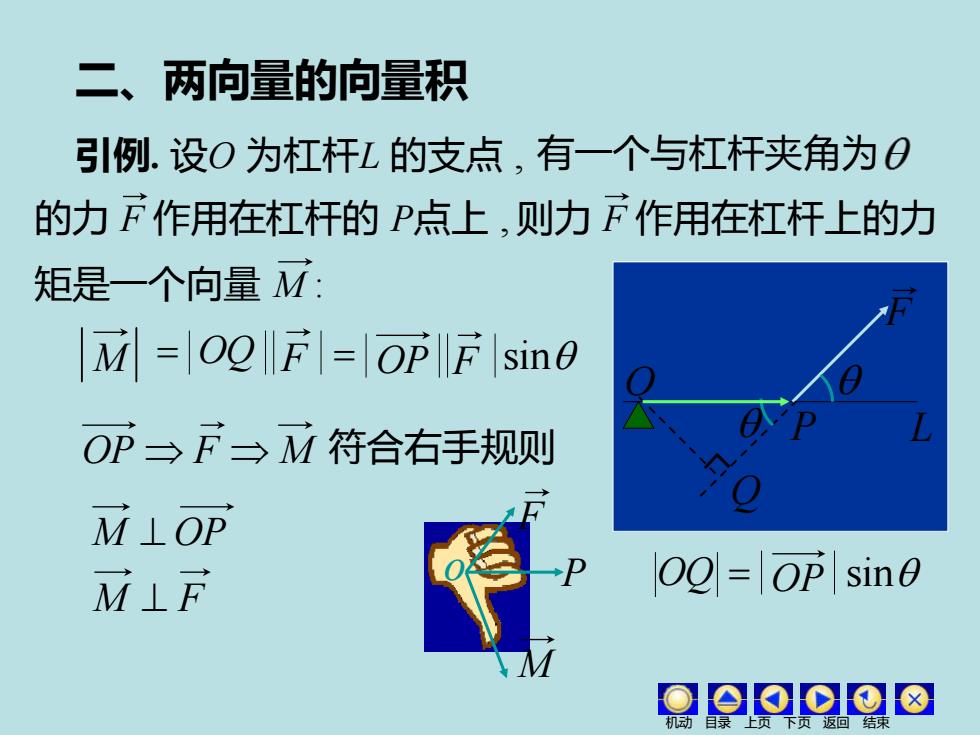
二、两向量的向量积 引例.设O为杠杆L的支点,有一个与杠杆夹角为0 的力F作用在杠杆的P点上,则力F作用在杠杆上的力 矩是一个向量M: M=0F=OpFsin0 OP三F三M符合右手规则 M⊥OP M上F 00=OP sine Oao⊙o8
二、两向量的向量积 引例. 设O 为杠杆L 的支点 , 有一个与杠杆夹角为 OQ = O P L Q 符合右手规则 = OQ F = OP F sin OP sin OP F M M ⊥ OP M 矩是一个向量 M : 的力 F 作用在杠杆的 P点上 , 则力 F 作用在杠杆上的力 F o P F M M ⊥ F 机动 目录 上页 下页 返回 结束