
还有种思路解释L(更简单) Laa是周期为T的偶函数,按偶函数分解傅氏级数 (只有余孩项,变化周期为π,只有偶函数) La=lo+1 cos 2a+la cos4a+. ■根据假设,定子绕组在空间产生正弦分布磁动势 (不计谐波,自感也是正弦形式,忽略四次及以上分量) L=lo +12 cos2a 2025/5/16 电力系统分析第三章同步发电机的基本方程 16
2025/5/16 电力系统分析 第三章 同步发电机的基本方程 16 ◼ Laa是周期为π的偶函数,按偶函数分解傅氏级数 (只有余弦项,变化周期为π,只有偶函数) ◼ 根据假设,定子绕组在空间产生正弦分布磁动势 (不计谐波,自感也是正弦形式,忽略四次及以上分量) cos 2 cos 4 . Laa = l 0 +l 2 +l 4 + Laa = l 0 +l 2 cos2 还有种思路解释Laa(更简单)
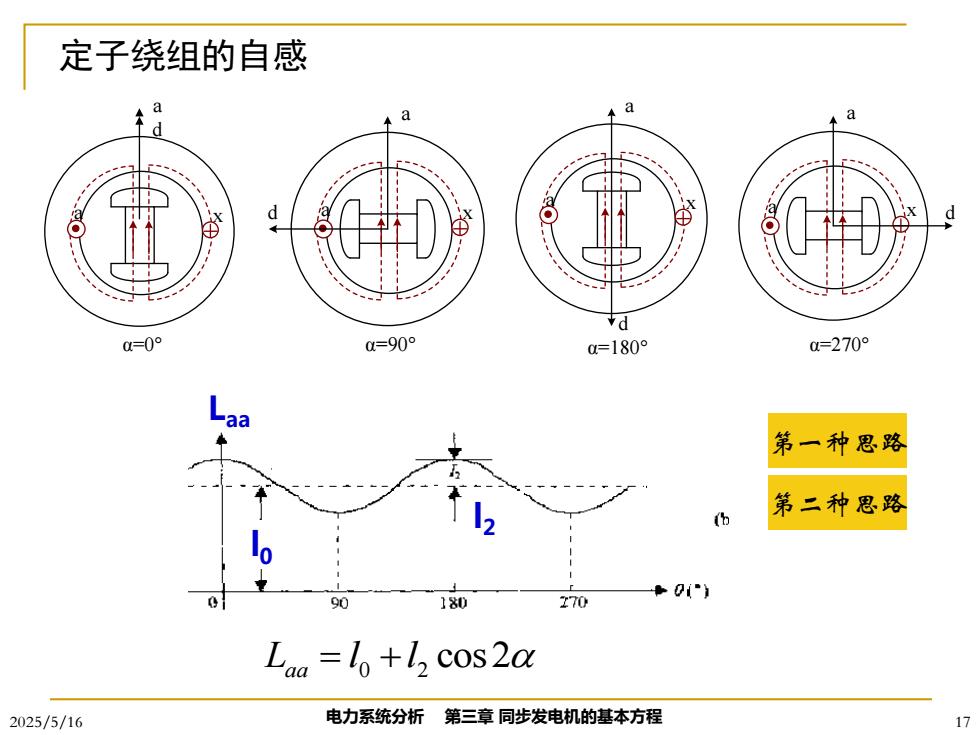
定子绕组的自感 a d a=0° 0u=90° a=180° 0=270° aa 第一种思路 第二种思路 b ◆01”) 90 180 270 Laa =lo+l cos 2a 2025/5/16 电力系统分析第三章同步发电机的基本方程
2025/5/16 电力系统分析 第三章 同步发电机的基本方程 17 a x a d α=0° a x a α=90° d a x a α=180° d a x a α=270° d 定子绕组的自感 Laa l0 l2 第二种思路 第一种思路 Laa = l 0 +l 2 cos2

定子三相绕组对称,可得b、c相: Lb=1+I2cos2(a-120) Lc=1+l,c0s2(a+120) 注意: Loa =lo+l cos2a (1)l>l2,Laa>0 %=以-元)一,=0L.=常数 隐极机 九ad=九ag 一0 2025/5/16 电力系统分析第三章同步发电机的基本方程 18
2025/5/16 电力系统分析 第三章 同步发电机的基本方程 18 定子三相绕组对称,可得b、c相: cos 2( 120 ) cos 2( 120 ) 0 2 0 2 = + + = + − L l l L l l cc b b 注意: Laa = l 0 +l 2 cos2 (1)l 0 > l 2 ,Laa > 0 ( ) a d a q a a d a q l 隐极机 = ( ) 2 1 2 2 2 = − l 2 = 0⇒Laa = 常数 =l0

2.定子绕组间的互感系数 定子绕组的互感 ■a相电流产生交链于b相绕组的磁链 ya=06[pbao+4 ad COS(a-120)+ag sin(a-120°】 =0a06ia-元mo+元ad cosa cos(a-l20°)+元a sina sin(a-l20°)】 2025/5/16 电力系统分析第三章同步发电机的基本方程
2025/5/16 电力系统分析 第三章 同步发电机的基本方程 19 2.定子绕组间的互感系数 ◼ a相电流产生交链于b相绕组的磁链 [ cos cos( 120 ) sin sin( 120 )] [ cos( 120 ) sin( 120 )] = − + − + − = + − + − a b a m a d a q b a b b a a d a q i 定子绕组的互感
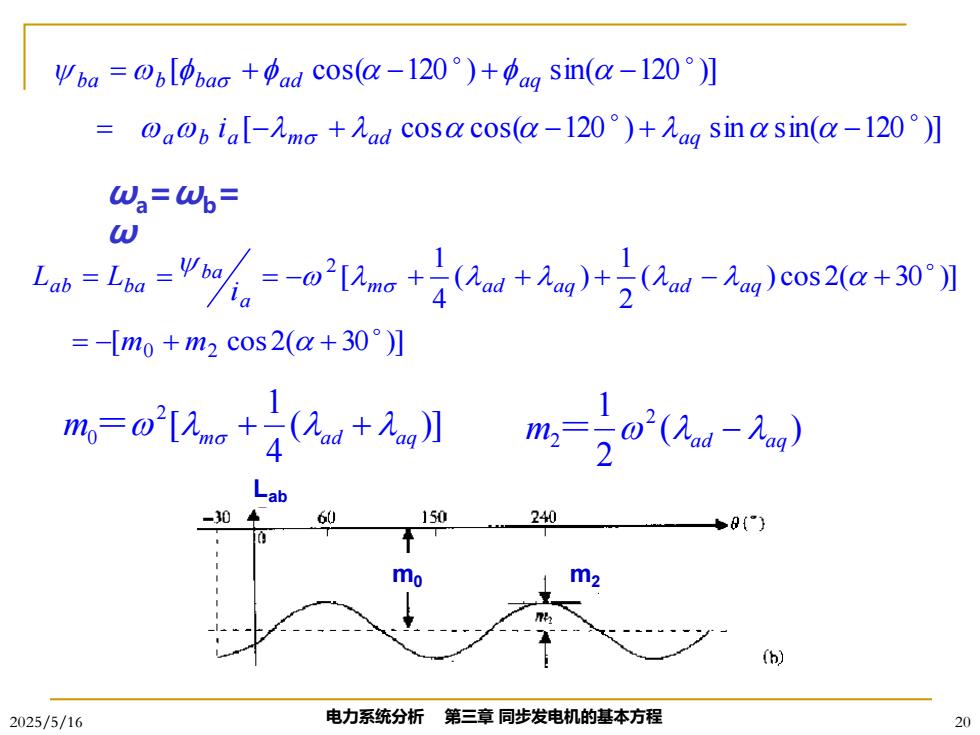
wba=06[pbao+padc0s(a-120°)+ag sin(a-120°】 =@a@pia[-元mo+2 ad cosa cos(a-l20°)+aa sin a sin(a-l20°] W3=Wb三 as((og)con2 1 =-[m0+m2c0s2(a+30°)】 m=o++元y】 m=o2(2-g) 050 240 mo m2 (h) 2025/5/16 电力系统分析第三章同步发电机的基本方程 20
2025/5/16 电力系统分析 第三章 同步发电机的基本方程 20 ωa =ωb= ω [ cos cos( 120 ) sin sin( 120 )] [ cos( 120 ) sin( 120 )] = − + − + − = + − + − a b a m a d a q b a b b a a d a q i [ cos 2( 30 )] ( ) cos 2( 30 )] 2 1 ( ) 4 1 [ 0 2 2 = − + + = = = − + + + − + m m i L L m a d a q a d a q a b a a b b a ( )] 4 1 [ 2 m0 = m + a d + a q ( ) 2 1 2 m2 = ad − aq m0 m2 Lab