tan20,=- 2Tx 2×50 1.429 Ox-Oy (-70)-0 27.5 62.5 03 城 因为。,<0,所以co=256卢omm对应 人置弘在 】 02+ 26MPa max min 96MPa g1=26MPa,o2=0,o3=-96MPa
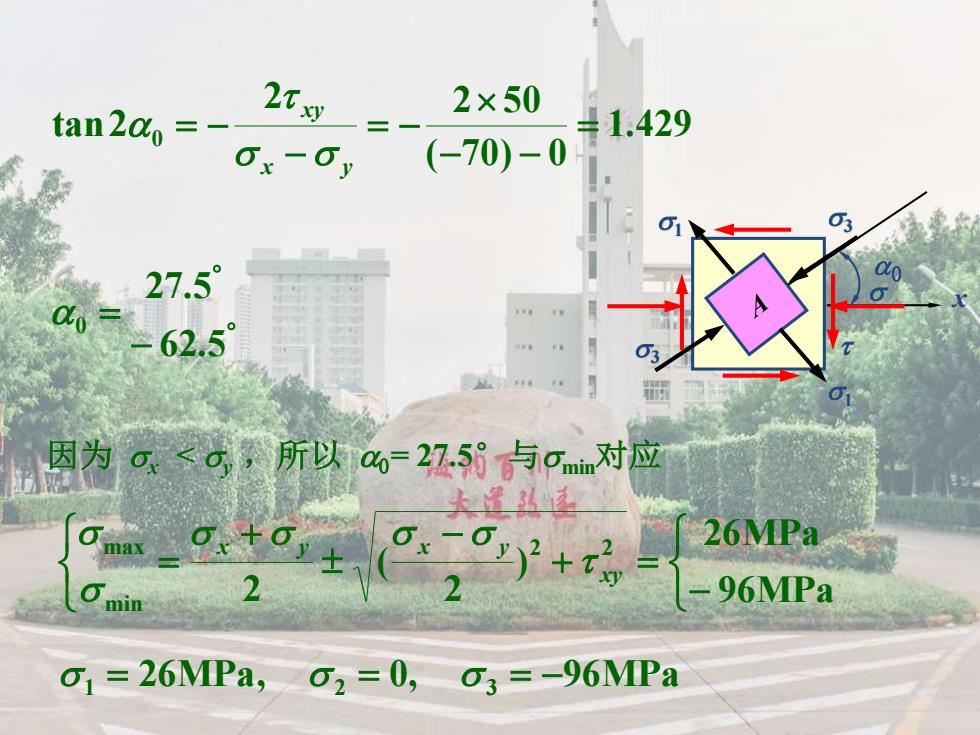
因为 x < y ,所以 0= 27.5°与 min对应 1.429 ( 70) 0 2 2 50 tan2 0 = − = − = x y xy − = 62 5 27 5 0 . . A x 0 − + = − + = MPa MPa ( ) min max 96 26 2 2 2 2 xy x y x y 26MPa, 0, 96MPa 1 = 2 = 3 = − 1 1 3 3
例题5图示单元体,已知g,=-40MPa,g, =60MPa,=-50MPa.试求e-f截面上的应力情 况及主应力和主单元体的方位。 解:(1)求ef截面上的应力 0-30 0x+0,0x- 丽用 2 2 cos2a-t sin 2 猫 40+60 40-60 c0s(-60°)-(-50)sim60° 2 2海附 -58.3MPa 大置莲 o-o,sin2a+cos2a =40-60 sin(-60) (-50)cos(-60°)=18.3MPa
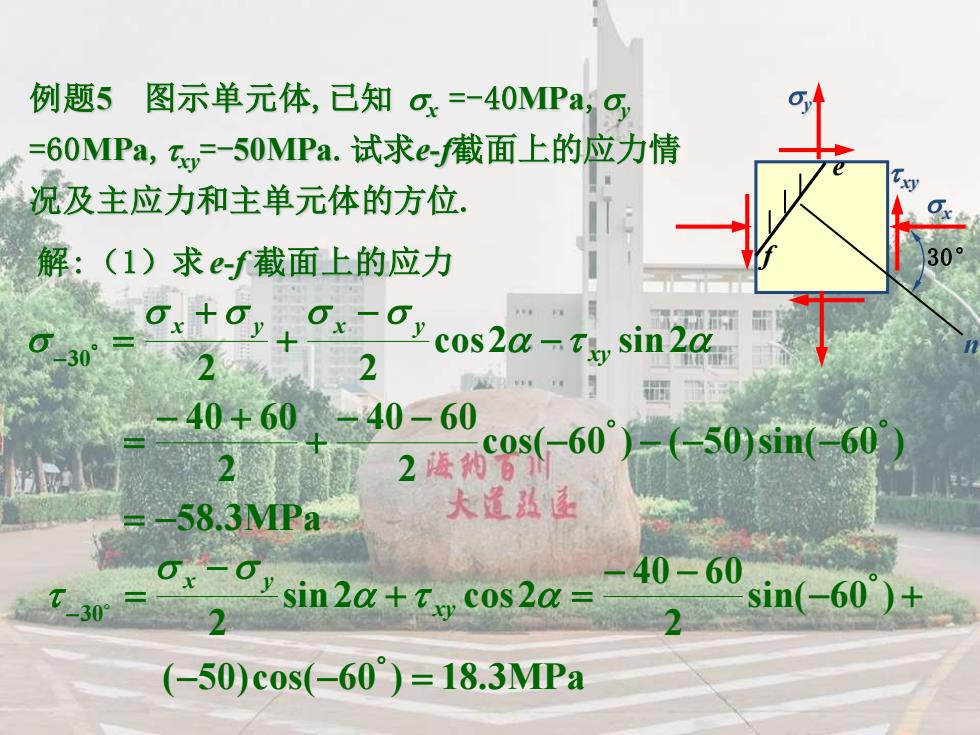
x y xy 例题5 图示单元体,已知 x =-40MPa,y =60MPa,xy =-50MPa.试求e-f截面上的应力情 况及主应力和主单元体的方位. n 30° e 解 f :(1)求e-f 截面上的应力 58.3MPa cos( 60 ) ( 50)sin( 60 ) 2 40 60 2 40 60 cos2 sin2 2 2 30 = − − − − + − = − − = − xy x y x y ( 50)cos( 60 ) 18.3MPa sin( 60 ) 2 40 60 sin2 cos2 2 30 − − = − + − + = − = − xy x y
(2)求主应力和主单元体的方位 2×(-50) tan2o=一 1-1 -40-60 3 Ox-Oy -45 22.5° 22.5 20= 00= 135 67.5 丽品 歪到 因为6<g,所以=-22.5°与gmim对应 细 max o.+Oy 80.7MPa 2大置弘图 =60.7MPa min o1=80.7MP 02=0 o3=-60.7MPa
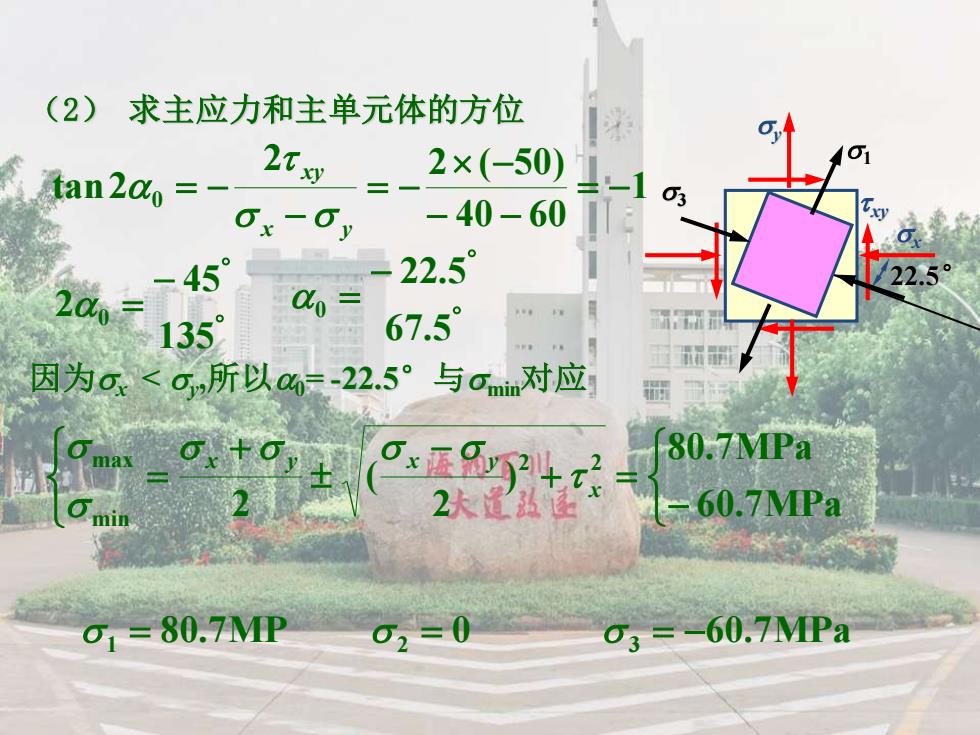
(2) 求主应力和主单元体的方位 1 40 60 2 2 50 2 0 = − − − = − = ( ) tan x y xy − = 135 45 20 − = 67 5 22 5 0 . . 因为x < y ,所以0= -22.5°与 min对应 − + = − + = 60.7MPa 80.7MPa ) 2 ( 2 2 2 min max x x y x y 1 = 80.7MP 2 = 0 3 = −60.7MPa x y xy 22.5° 1 3
例题6求平面纯剪切应力状态的主应力及主平面方位 解 (1)求主平面方位 2tx 03 tan 2@o =一 =-00 Ox-Oy 90° 45° 20 90 -45° 猫 因为GG且石>0腾所以%=-45°与o对应 (2)求主应力 大置玉 】 max Omin 2 1=T,02=0,C3=-t
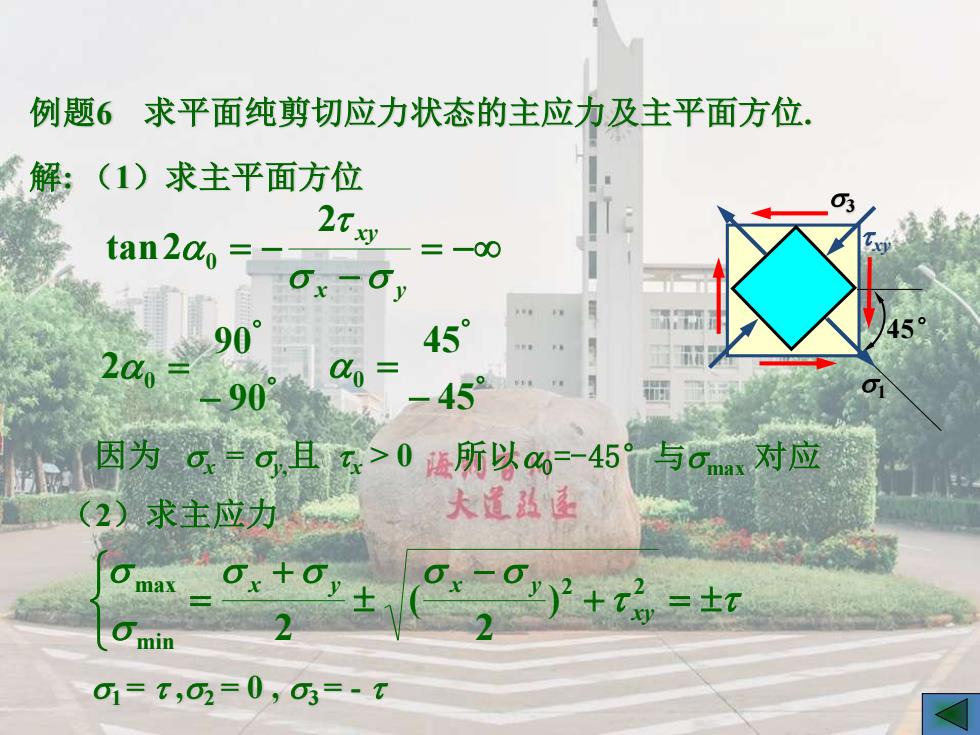
解: (1)求主平面方位 = − − = − x y xy 2 2 0 tan − = 90 90 20 − = 45 45 0 因为 x = y, 且 x > 0 例题6 求平面纯剪切应力状态的主应力及主平面方位. xy 所以0=-45°与 max 对应 45° (2)求主应力 + = − + = 2 2 2 2 xy x y x y ( ) min max 1 = ,2 = 0 , 3 = - 1 3

§7-3平面应力状态分析图解法 莫尔圆 将斜截面应力计算公式改写为 所闲品湖 Ox-Oy sin2a +ty cos2a 大置弘玉 把上面两式等号两边平方,然后相加便可消去%得
§7-3 平面应力状态分析-图解法 sin cos cos sin 2 2 2 2 2 2 2 xy x y xy x y x y + − = − − = + − 一、莫尔圆 将斜截面应力计算公式改写为 把上面两式等号两边平方,然后相加便可消去,得 2 2 2 2 2 2 xy x y x y + − + = + ( − ) ( )