
材料力学教索第9讲教学方案圆轴扭转时的变形和刚度条件非圆截面杆的扭转基本圆轴扭转时的变形和刚度条件、矩形截载面杆扭转时的应力与变内形。容1、掌握圆轴扭转时变形及变形程度的描述与计算。教学掌握刚度条件的建立及利用刚度条件进行相关计算。2、目3、了解圆柱形密圈螺旋弹簧的应力和变形计算。的4、了解矩形截面杆扭转时的横截面上的应力分布与变形计算。重点本节重点:圆轴扭转时变形及变形程度的描述与计算,刚度条件的建立及相关计算。难点本节难点:对圆轴变形程度的理解
材 料 力 学 教 案 1 第 9 讲 教学方案 ——圆轴扭转时的变形和刚度条件 非圆截面杆的扭转 基 本 内 容 圆轴扭转时的变形和刚度条件、矩形截面杆扭转时的应力与变 形。 教 学 目 的 1、掌握圆轴扭转时变形及变形程度的描述与计算。 2、掌握刚度条件的建立及利用刚度条件进行相关计算。 3、了解圆柱形密圈螺旋弹簧的应力和变形计算。 4、了解矩形截面杆扭转时的横截面上的应力分布与变形计算。 重 点 、 难 点 本节重点:圆轴扭转时变形及变形程度的描述与计算,刚度条件的建 立及相关计算。 本节难点:对圆轴变形程度的理解

进s3-5圆轴扭转时的变形和刚度条件扭转角是指受扭构件上两个横截面绕轴线的相对转角。对于圆轴,由式(4-10)do=TdGI,所以TIITΦ=[d=(4-17)(rad)dxJoGI.GI.式中GI称为圆轴的抗扭刚度,它为剪切模景与极惯性短乘积。GI,越大,则扭转角越小。7让9=4%/%,为单位长度相对扭角,则有=(rad/m)GI.扭转的刚度条件:9m=l, ≤[0l rad/m)(4-18)二×180 ≤[0] (° /m)或(4-19)Pmar"Gl*元例3-3如图4-13的传动轴,n=500T/min,N,=500马力,N,=200马力,N,=300马力,已知[]=70MPa,[o]-1°/m,G=80GPa。求:确定AB和BC段直径。解:1)计算外力偶矩N2Nm,=7024N7024(N·m)m =7024=2809.6 (N·m)400200(a)me- 7024-42144 (N m)4214.4N.m作扭矩T图,如图4-13b所示。2)计算直径d7024N·m(b)AB段:由强度条件,图4-13
第 九 讲 2 §3-5 圆轴扭转时的变形和刚度条件 扭转角是指受扭构件上两个横截面绕轴线的相对转角。对于圆轴,由式(4-10) GI p Tdx d = 所以 p l 0 p l GI Tl dx GI T = d = = (rad) (4-17) 式中 GI p 称为圆轴的抗扭刚度,它为剪切模量与极惯性矩乘积。 GI p 越大,则扭转角 越小。 让 dx d = ,为单位长度相对扭角,则有 GI p T = (rad/m) 扭转的刚度条件: = P max GI T (rad/m) (4-18) 或 = 180 GI T P max (°/m) (4-19) 例 3-3 如图 4-13 的传动轴, n = 500 r/min,N1 = 500 马力, N2 = 200 马力, N3 = 300 马力,已知 = 70 MPa,=1°/m,G = 80 GPa。求:确定 AB 和 BC 段直径。 解: 1)计算外力偶矩 7024 7024 1 = = n N mA (N·m) 7024 2809.6 2 = = n N mB (N·m) 7024 4214.4 3 = = n N mC (N·m) 作扭矩 T 图,如图 4-13b 所示。 2)计算直径 d AB 段:由强度条件
材料力学教索16T≤[]Taw"W."d16T16×7024d,>~80 (mm)=元×70×10%V元[]由刚度条件Tx180° ≤[0]β=Gd元3232×7024×/8032T×180=84.6(mm)d,≥Gn'[0]=80×10x元×l取d,=84.6mmBC段:同理,由扭转强度条件得d,≥67mmd,≥74.5mm由扭转刚度条件得取d,=74.5mmCmomo例3-4如图414所示等直圆杆,已知aaam。=10KN·m,试绘扭矩图。(a)解:设两端约束扭转力偶为ma,m(1)由静力平衡方程Zm=0得(b)ma-mo+mo-mg=0(a)ma=mBo此题属于一次超静定。一m(2)由变形协调方程(可解除B端约束),用变形叠Imo图4-14加法有
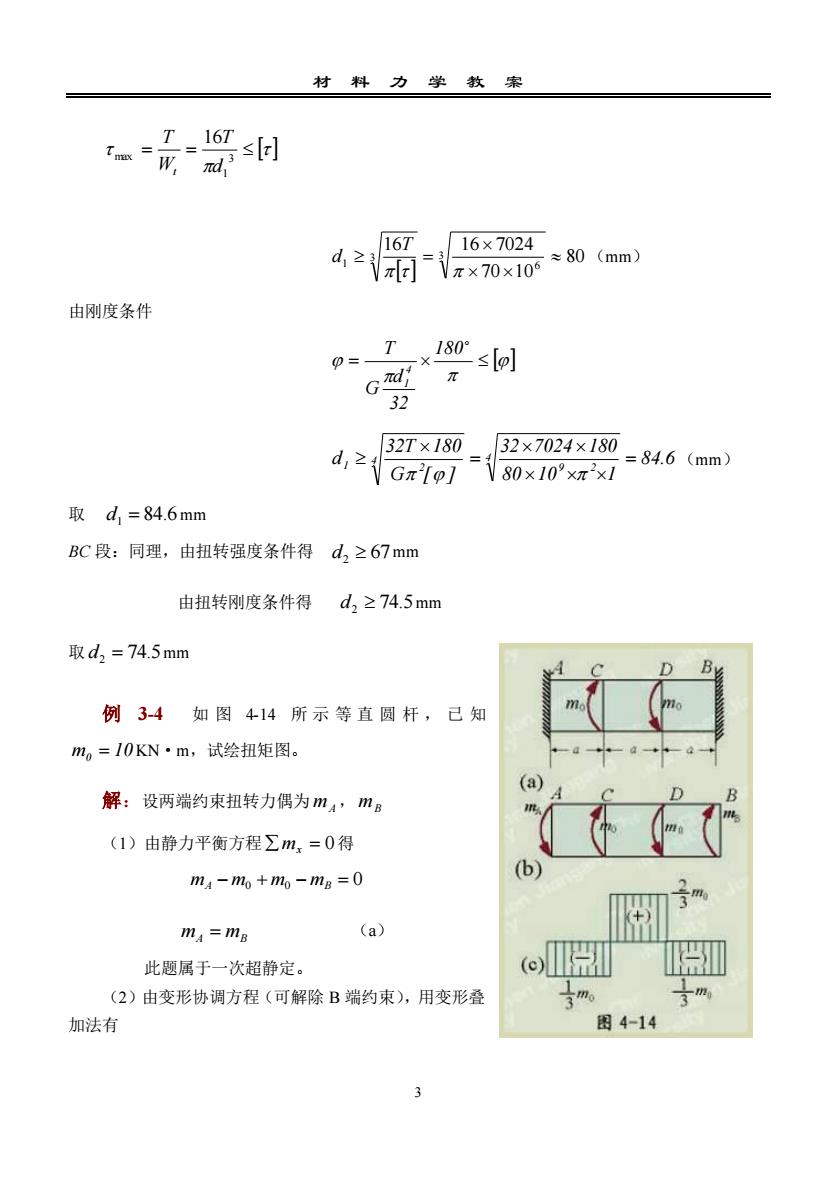
材 料 力 学 教 案 3 = = 3 1 max 16 d T W T t 80 70 10 16 16 7024 3 6 3 1 = T d (mm) 由刚度条件 = 180 32 d G T 4 1 84.6 80 10 1 32 7024 180 G [ ] 32T 180 d 4 9 2 4 1 2 = = (mm) 取 d1 = 84.6 mm BC 段:同理,由扭转强度条件得 d2 67 mm 由扭转刚度条件得 d2 74.5 mm 取 d2 = 74.5 mm 例 3-4 如 图 4-14 所 示 等 直 圆 杆 , 已 知 m0 = 10 KN·m,试绘扭矩图。 解:设两端约束扭转力偶为 mA, mB (1)由静力平衡方程 mx = 0 得 mA − m0 + m0 − mB = 0 mA = mB (a) 此题属于一次超静定。 (2)由变形协调方程(可解除 B 端约束),用变形叠 加法有

第九讲(b)中n =中, -中, +中, =0(3)物理方程-mg-3a-mo'a +m2a(c)中B,=", ΦB, =中BGI,GI,GI,由式(c),(b)得- moa+ mg-2a_ "g:3a =0GI,"GI,GI,即-mg+2mo-3mg=0并考虑到(a),结果m,=ma=m13假设的力偶转向正确,绘制扭矩图如图4-14c所示s3-6圆柱形密圈螺旋弹簧的应力和变形计算螺旋弹簧如图4-15a 所示。当螺旋角α<5°时,可近似认为簧丝的横截面与弹簧轴线在同一平面内1.弹簧丝横截面上的应力(d)0图4-15爆设弹簧如图4-15b以簧丝的任意横截面取出密圈弹簧的上部分为研究对象,根据平衡方程,横截面上剪由Q引起的剪应=只,需且认为"均匀分布于横截面上(图410):荐支整力更另视为直样的我扭转引起的最大应力(图415)一18一岁Q=P,扭短T=_PD。,一般将这种弹簧称为密圈螺旋弹簧。4
第 九 讲 4 0 B B1 B2 B3 = − + = (b) (3)物理方程 p 0 B GI m a 1 − = , p 0 B GI m 2a 2 + = , p B B GI m 3a 3 − = (c) 由式(c),(b)得 0 GI m 3a GI m 2a GI m a p B p 0 p 0 = − + − 即 − m0 + 2m0 − 3mB = 0 并考虑到(a),结果 3 m m m 0 A = B = 假设的力偶转向正确,绘制扭矩图如图 4-14c 所示。 §3-6 圆柱形密圈螺旋弹簧的应力和变形计算 螺旋弹簧如图 4-15a 所示。当螺旋角 5 时,可近似认为簧丝的横截面与弹簧轴线在同一平面 内 1.弹簧丝横截面上的应力 如图 4-15b 以簧丝的任意横截面取出密圈弹簧的上部分为研究对象,根据平衡方程,横截面 上剪力由 Q 引起的剪应力 1 2 4 d P A Q = = ,而且认为 1 均匀分布于横截面上(图 4-15c);若将 簧丝的受力视为直杆的纯扭转,由 T 引起的最大剪应力(图 4-15d) 2 3 3 16 8 d PD d T W T t = = = Q = P ,扭矩 T PD 2 1 = 。,一般将这种弹簧称为密圈螺旋弹簧

材料力学教索所以在簧丝横截面内侧A点有8PDG1+=^8PD(4-20)Tmx =t,+t,d3+2DJdh=/+d其中(4-21)2D当%</10,略去剪应力t,所引起的误差T<5%,可用近似式8PD(4-22)元d3对某些工程实际问题,如机车车辆中的重弹簧,%的值并不太小,此时不仅要考虑剪力,还要考虑弹簧丝曲率的影响,进一步理论分析和修正系数k的选取可见有关参考书。密圈弹簧丝的强度条件是Tm ≤[3](4-23)式中:[]一弹簧丝材料的许用剪应力2(b)(c)(a)图4-16弹簧变形2.弹簧的变形设弹簧在轴向压力(或拉力)作用下,轴线方向的总缩短(或伸长)量为入,这是弹簧的整体的压缩(或拉伸)变形。如图4-16a、b,外力对弹簧做功W=P入。簧丝横截面上,距圆心为p的任意点的扭转剪应力为
材 料 力 学 教 案 5 所以在簧丝横截面内侧 A 点有 max 1 2 3 3 8 2 1 8 d PD k D d d PD = = + = + (4-20) 其中 2D d k = 1 + (4-21) 当 10 1 D d ,略去剪应力 1 所引起的误差 0 0 5 ,可用近似式 max 3 d 8PD = (4-22) 对某些工程实际问题,如机车车辆中的重弹簧, D d 的值并不太小,此时不仅要考虑剪力,还 要考虑弹簧丝曲率的影响,进一步理论分析和修正系数 k 的选取可见有关参考书。 密圈弹簧丝的强度条件是 max (4-23) 式中: —弹簧丝材料的许用剪应力 2. 弹簧的变形 设弹簧在轴向压力(或拉力)作用下,轴线方向的总缩短(或伸长)量为 ,这是弹簧的整 体的压缩(或拉伸)变形。如图 4-16a、b,外力对弹簧做功 P 2 1 W = 。簧丝横截面上,距圆心 为 的任意点的扭转剪应力为