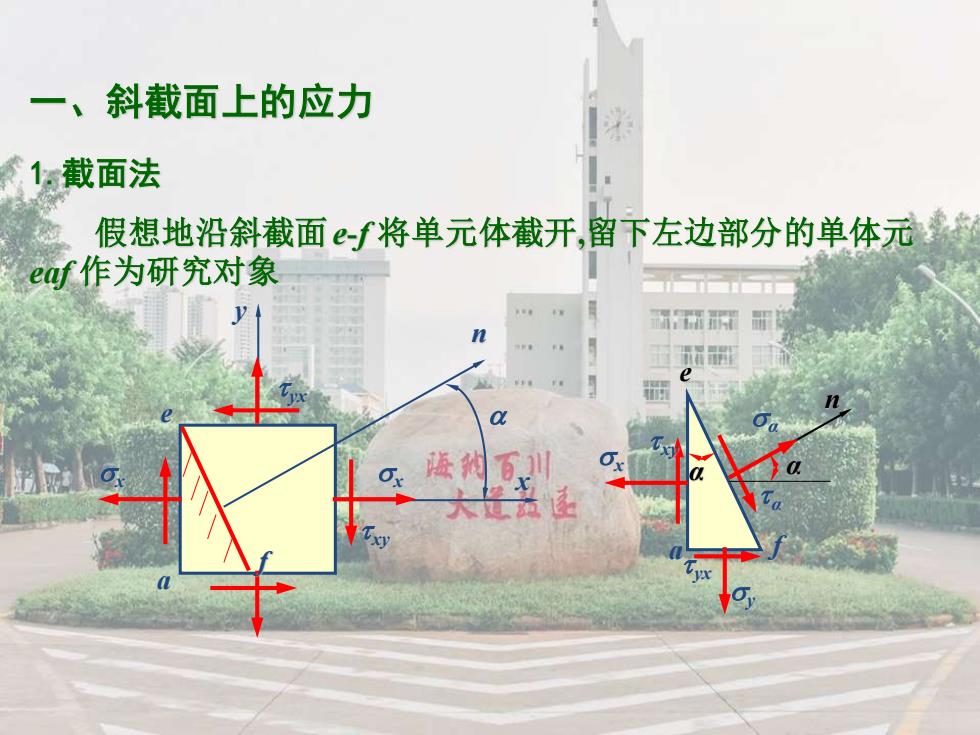
一、斜截面上的应力 1截面法 假想地沿斜截面f将单元体截开,留下左边部分的单体元 eof作为研究对象 所闲 e 城 德闪百
一、斜截面上的应力 1.截面法 假想地沿斜截面e-f 将单元体截开,留下左边部分的单体元 eaf 作为研究对象 x y a x x yx xy e f n e a f x xy yx y α α α n α
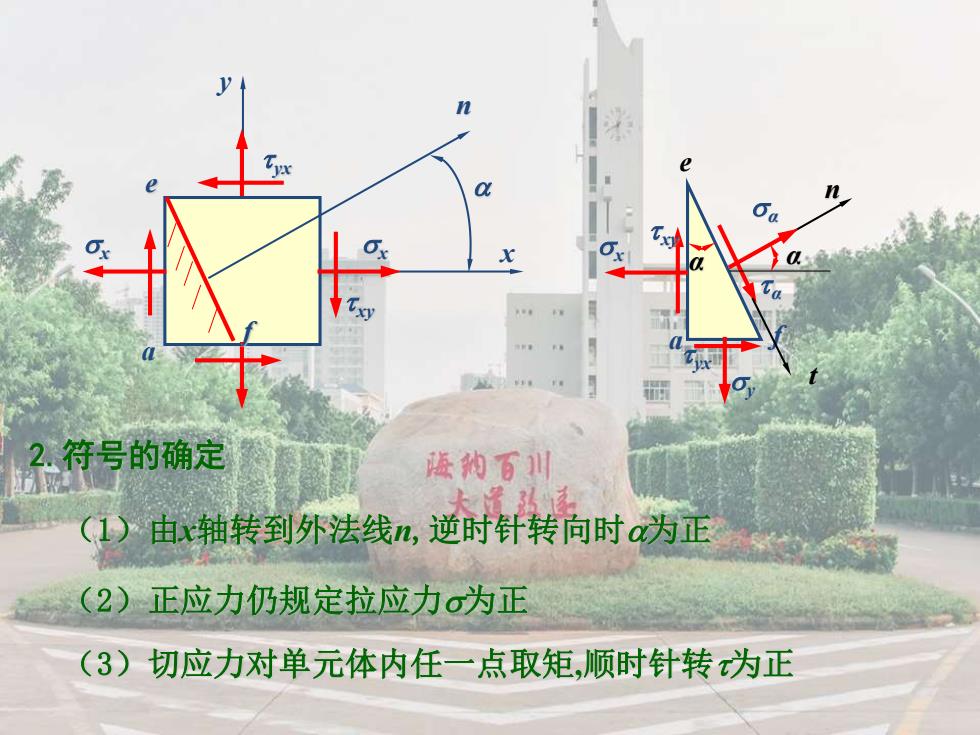
n n 子符号的确定 德纳百川 3 (1)由x轴转到外法线n,逆时针转向时a为正 (2)正应力仍规定拉应力σ为正 (3)切应力对单元体内任一点取矩,顺时针转为正
x y a x x yx xy e f n (1)由x轴转到外法线n,逆时针转向时为正 (2)正应力仍规定拉应力为正 (3)切应力对单元体内任一点取矩,顺时针转为正 2.符号的确定 e a f x xy yx y α α α n α t
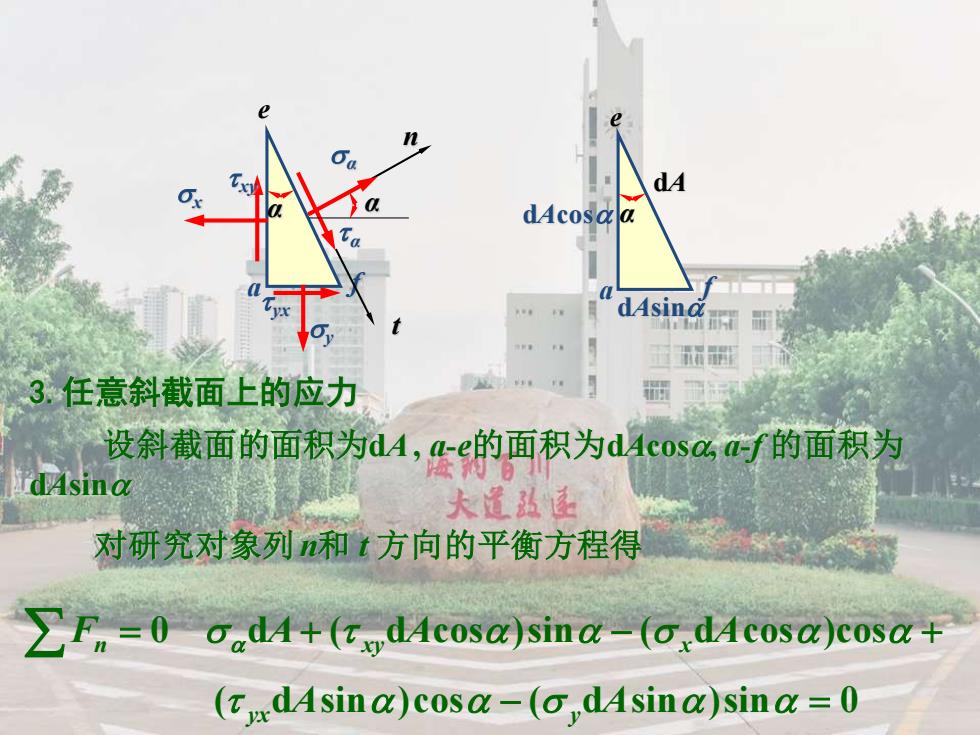
n dAcosaa dAsina时 3任意斜截面上的应力 设斜载面的面积大d4,g9的面积为4coso%/的面积为 dAsin 大置弘 对研究对象列n和t方向的平衡方程得 F=0ad4+(tsdAcosa)sina-(o,dAcosa)cosa+ (tdAsina)cosa-(o,dAsina)sina=0
设斜截面的面积为dA, a-e的面积为dAcos, a-f 的面积为 dAsin e a f x xy yx y α α α n α e a f α dA dAsin dAcos 3.任意斜截面上的应力 对研究对象列n和 t 方向的平衡方程得 ( d sin )cos ( d sin )sin 0 0 d ( d cos )sin ( d cos )cos − = = + − + A A F A A A yx y n xy x t

>F=0 todA-(,dAcosa)cosa-(o.dAcosa)sina+ (dAsina)sina+(o dAsina)cosa =0 化简以上两个平衡方程最后得 新霜用 x十OyOx-O cos2a-7 5i2a a-oasin2ac0s2a 2 大 不难看出。+0+0=x+0) 即两相互垂直面上的正应力之和保持一个常数
sin2 cos2 2 cos2 sin2 2 2 xy x y xy x y x y + − = − − = + ( d sin )sin ( d sin )cos 0 0 d ( d cos )cos ( d cos )sin + = = − − + A A F A A A yx y t xy x 化简以上两个平衡方程最后得 不难看出 + = x + y +90 即两相互垂直面上的正应力之和保持一个常数

二、最大正应力及方位 x+-y cos2asin2a 2 O- sin 2a+txy cos2a 研品得 个.最大正应力的方位(The direction of maximum normal stress) 可ysiǚ2o年t x cos2a1=0 大道弘留 00 tan2ao O.-O a+90 和+90°确定两个互相垂直的平面,一个是最大正应力 所在的平面,另一个是最小正应力所在的平面
二、最大正应力及方位 1.最大正应力的方位(The direction of maximum normal stress ) 令 2 2 2 2 2 2 2 sin cos cos sin xy x y xy x y x y + − = − − = + sin2 cos2 ] 0 2 2[ d d + = − = − xy x y = − − 0 2 tan2 xy x y + 0 90 0 0 和 0+90°确定两个互相垂直的平面,一个是最大正应力 所在的平面,另一个是最小正应力所在的平面