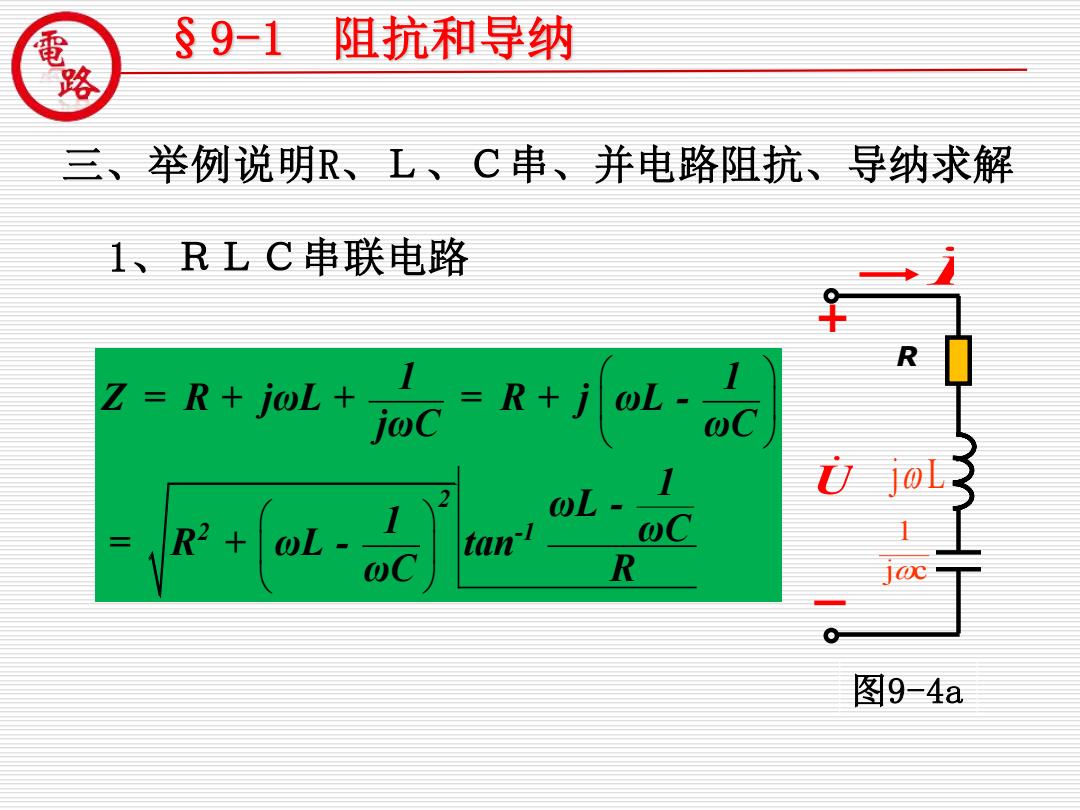
§9-1 阻抗和导纳 三、举例说明R、L、C串、并电路阻抗、导纳求解 1、RLC串联电路 R Z=R+joL+ cc R+ tan R 图9-4a
三、举例说明R、L、C串、并电路阻抗、导纳求解 2 2 -1 1 1 Z = R + jωL + = R + j ωL - jωC ωC 1 ωL - 1 ωC = R + ωL - tan ωC R 图9-4a 1、RLC串联电路 R + _ j c 1 U j L I §9-1 阻抗和导纳

§9-1 阻抗和导纳 说明:Z的电阻分量一一R 的电抗分量一z三0L0事 Z() 0L> 呈感性 OC OL. o=tan oc=o(o)> 呈中性 R oL≤ 呈容性 C
( ) 1 z = ωL - = z ω ωC 说明: Z的电阻分量――R Z的电抗分量―― ( ) ( ) 2 2 -1 1 Z = R + ωL - = Z ω ωC 1 ωL > 1 ωC ωL - ωC 1 φ = tan = φ ω ωL = R ωC 1 ωL < ωC 呈感性 呈中性 呈容性 §9-1 阻抗和导纳
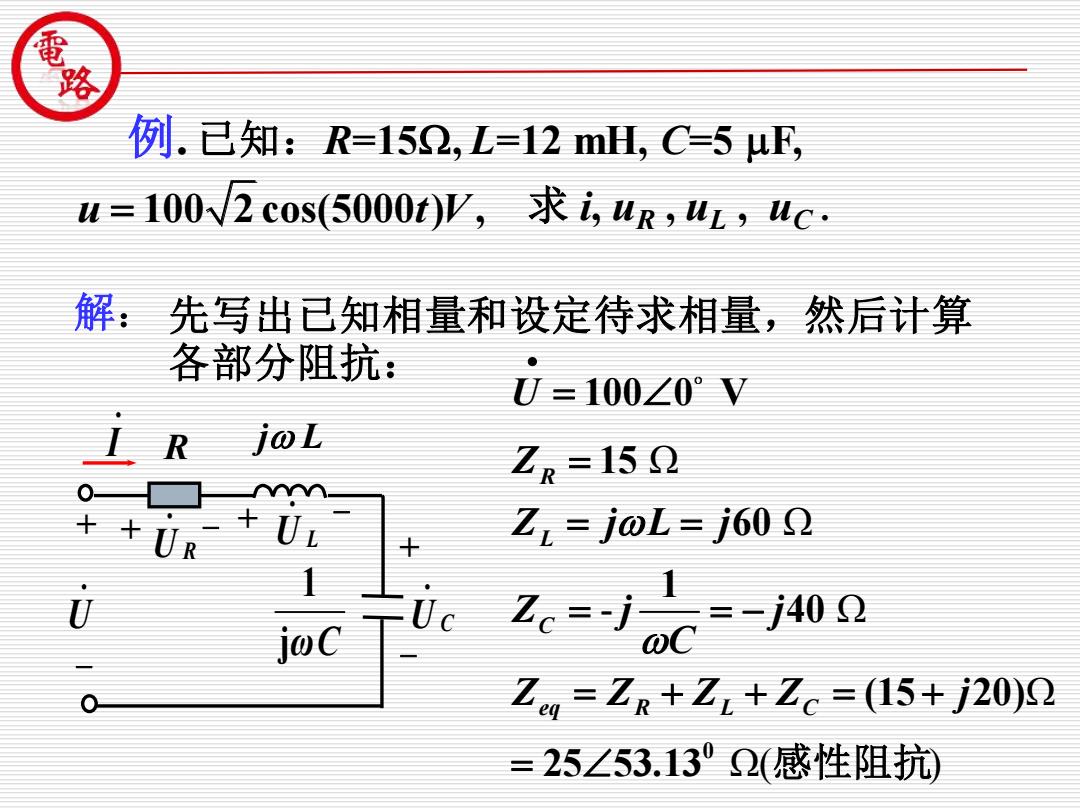
例.已知:R=152,L=12mH,C=5μE u=100N2cos5000t)Ψ,求i,ur,uz,uc, 解:先写出已知相量和设定待求相量,然后计算 各部分阻抗 ● 0=100∠0°V ZR=152 ++UR Z=joL=j600 joC 下Uc 五==-4wn Zg=ZR+Z+Zc=(15+j20)2 =25∠53130Q(感性阻抗
例. 已知:R=15, L=12 mH, C=5 F, u t V = 100 2 cos(5000 ) , 求 i, uR , uL , uC . 解: 先写出已知相量和设定待求相量,然后计算 各部分阻抗: U 100 0 V • = Ω Ω - Ω Ω Ω( ) 0 15 60 1 40 (15 20) 25 53.13 R L C eq R L C Z Z j L j Z j j C Z Z Z Z j = = = = = − = + + = + = 感性阻抗 . I R j L + - + - + - . U U L . U C . jωC 1 + - U R

i-U 100∠0° =4∠-53.13°A 25∠53.13 dR=Ri=60L-53.13Y U1=joL1=240Z36.87°V ie议i6w☑-188y 则i=4W2cos(5000t-53.3)A 4=60N2cos(50001-53.13)V 4,=240V2cos(50001+36.87)V uc=160W2cos(5000t-143.13)V
o o o o o o 100 0 4 53.13 A 25 53.13 60 53.13 V 240 36.87 V 1 160 143.13 V C eq R L C U I Z U R I U j L I U j I • • • • • • • • = = = − = == − = = = − = − 则 5000 5000 5000 5000 o o o o 4 2 cos 53.13 A ( ) 60 2 cos( 53.13 ) V 240 2 cos( 36.87 ) V 160 2 cos( 143.13 ) V R L C i t u t u t u t = − = − = + = −
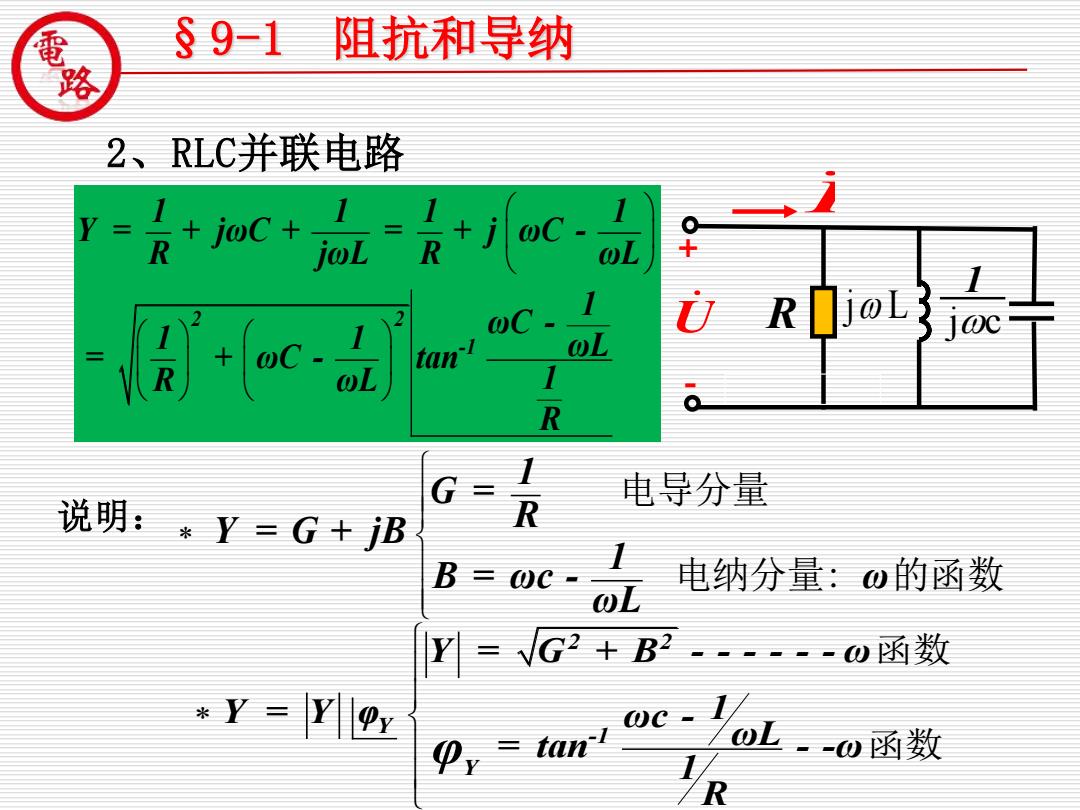
§9-1 阻抗和导纳 2、RLC并联电路 Y +oc+R+joc @C tan L R G= 电导分量 说明:*了=G+B R B0c-人 电纳分量:w的函数 Y=G2+B2一w函数 *Y= oc-oL.o函数
2 2 -1 1 1 1 1 Y = + jωC + = + j ωC - R jωL R ωL 1 ωC - 1 1 ωL = + ωC - tan R ωL 1 R + - R jc 1 j L I U 1 G = R Y = G + jB 1 B = ωc - ω ωL 电导分量 电纳分量: 的函数 2 2 Y -1 Y Y = G + B - - - - - - ω Y = Y φ ωc - 1 ωL = tan - -ω 1 R φ 函数 函数 说明: §9-1 阻抗和导纳 2、RLC并联电路