
3.稳定平衡和不稳定平衡
3. 稳定平衡和不稳定平衡

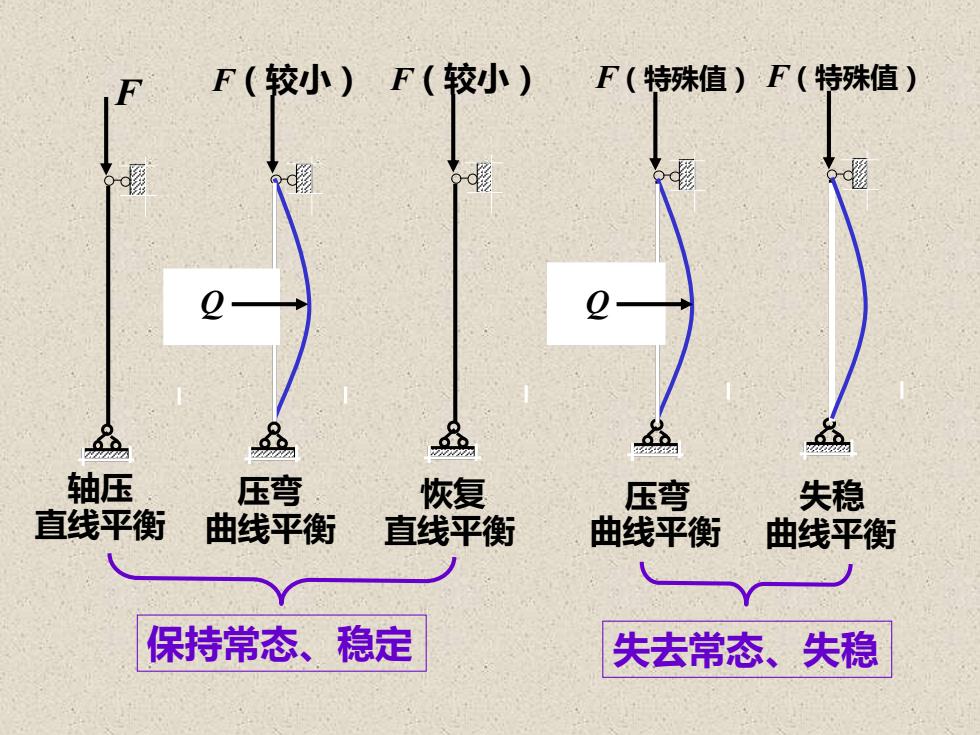
二、压杆失稳与临界压力:1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用2.压杆的稳定平衡与不稳定平衡:
二、压杆失稳与临界压力 : 1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。 2.压杆的稳定平衡与不稳定平衡:
F(较小)F(较小)F(特殊值)F(特殊值)FQQ88&轴压压弯恢复失稳压弯直线平衡曲线平衡直线平衡曲线平衡曲线平衡保持常态、稳定失去常态、失稳
F 轴压 F(较小) 压弯 F(较小) 恢复 直线平衡 曲线平衡 直线平衡 Q F(特殊值) 压弯 失稳 曲线平衡 曲线平衡 F(特殊值) 保持常态、稳定 失去常态、失稳 Q Q Q

压杆失稳的现象:1.轴向压力较小时,杆件能保持稳定的直线平衡状态:2.轴向压力增大到某一特殊值时,直线不再是杆件唯一的平衡状态;稳定:理想中心压杆能够保持稳定的(唯一的)直线平衡状态;(Stable )失稳:理想中心压杆丧失稳定的(唯一的)直O线平衡状态;(Unstable)临界力压杆失稳时,两端轴向压力的特殊值(Critical force)
压杆失稳的现象: 1. 轴向压力较小时,杆件能保持稳定的直线平衡状态; 2. 轴向压力增大到某一特殊值时,直线不再是杆件唯 一的平衡状态; 稳定: 理想中心压杆能够保持稳定的(唯一的) (Stable) 直线平衡状态; 失稳: 理想中心压杆丧失稳定的(唯一的)直 (Unstable) 线平衡状态; 临界力 压杆失稳时,两端轴向压力的特殊值 (Critical force)

S9-2细长中心受压直杆临界力的欧拉公式思路:假设压杆在某个压力F作用下在曲线状态平衡,然后设法去求挠曲函数。若:1)求得的挠曲函数=0,说明只有直线平衡状态;2)求得不为零的挠曲函数,说明压杆的确能够在曲线状态下平衡,即出现失稳现象
§9-2 细长中心受压直杆临界力的欧拉公式 思路: 假设压杆在某个压力Fcr作用下在曲线状态 平衡, 1)求得的挠曲函数≡0, 2)求得不为零的挠曲函数, 然后设法去求挠曲函数。若: 平衡状态; 说明只有直线 确能够在曲线状态下平衡, 说明压杆的 稳现象。 即出现失