例 图示为电容放电电路, 电容原先带有电压U。, 求开关闭合后电容电压随时间的变化。 解 Ri+u.=0(t≥0) R .=0 dt 特征根方程: RCp+1=0→ P=-1/RC 得通解: u(t)=kem=ke I 代入初始条件得:k=U。→ u,(t)=Ue Rc 说明在动态电路的分析中,初始条件是得到确 定解答的必需条件
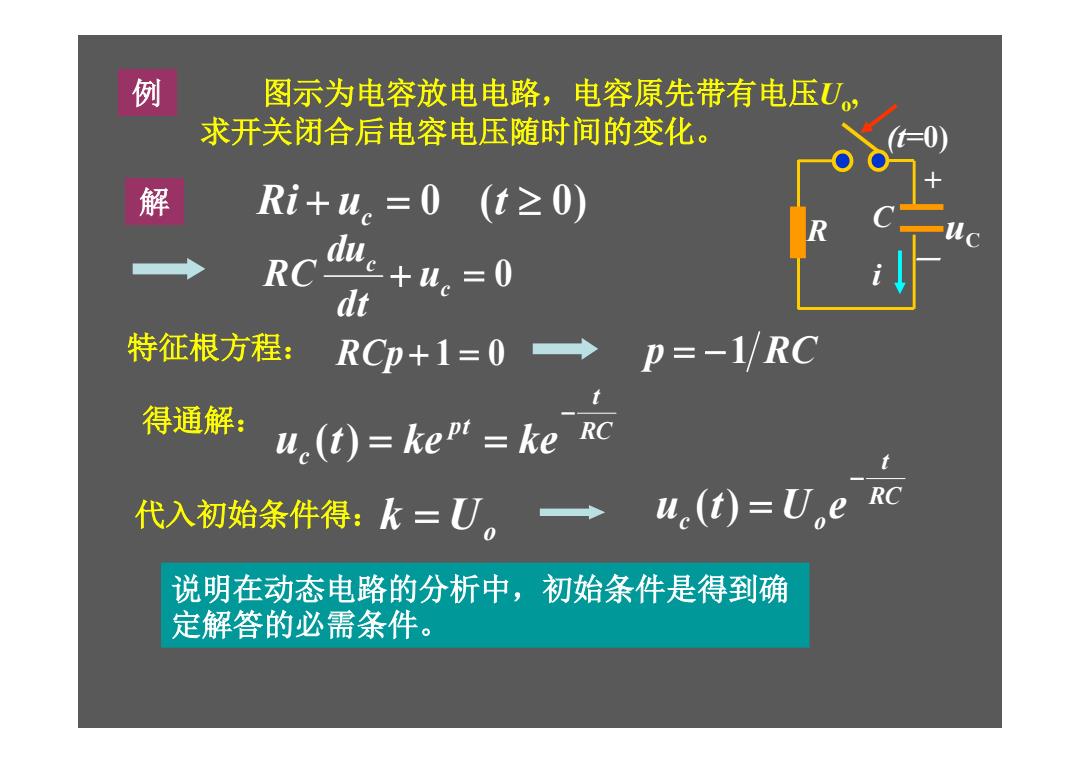
图示为电容放电电路,电容原先带有电压Uo , 求开关闭合后电容电压随时间的变化。 例 R -+ C i uC (t=0) 解 0 c c u dt du RC Ri u 0 (t 0) c 特征根方程: RCp 1 0 p 1 RC 得通解: Uo k RC t pt c u t ke ke ( ) 代入初始条件得: RC t c o u t U e ( ) 说明在动态电路的分析中,初始条件是得到确 定解答的必需条件
(2)电容的初始条件 :d=25a5 =255+265a5 =0)+C i(5)d5 t=0时刻 -0)=.0+G 当i)为有限值时 uc(0+)=uc(0-) 电荷 q=Cuc 守恒 9(0)=q(0-) 结 换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变
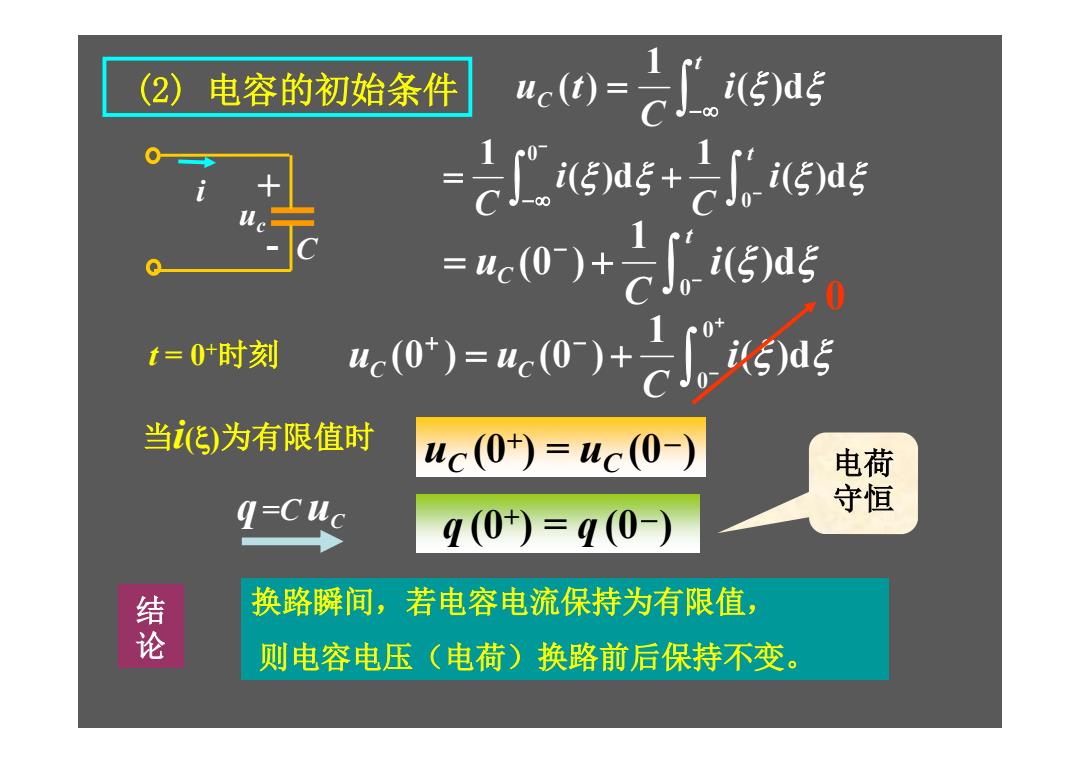
( )d 1 ( ) t C i C u t ( )d 1 ( )d 1 0 0 t i C i C ( )d 1 (0 ) 0 t C i C u t = 0+ 时刻 ( )d 1 (0 ) (0 ) 0 0 i C uC uC 当i()为有限值时 i uc C + - q (0+ ) = q (0-) uC (0+ ) = uC (0-) 换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。 (2) 电容的初始条件 0 q =C uC 电荷 守恒 结 论
(3)电感的初始条件 ,国=∫u) agas+a55 =,0)+24(5d5 0)=0)+鸣 ●0 t=0时刻 当为有限值时 (0+)=(0) 磁链 守恒 4(0+)=4(0-) 结论 换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变
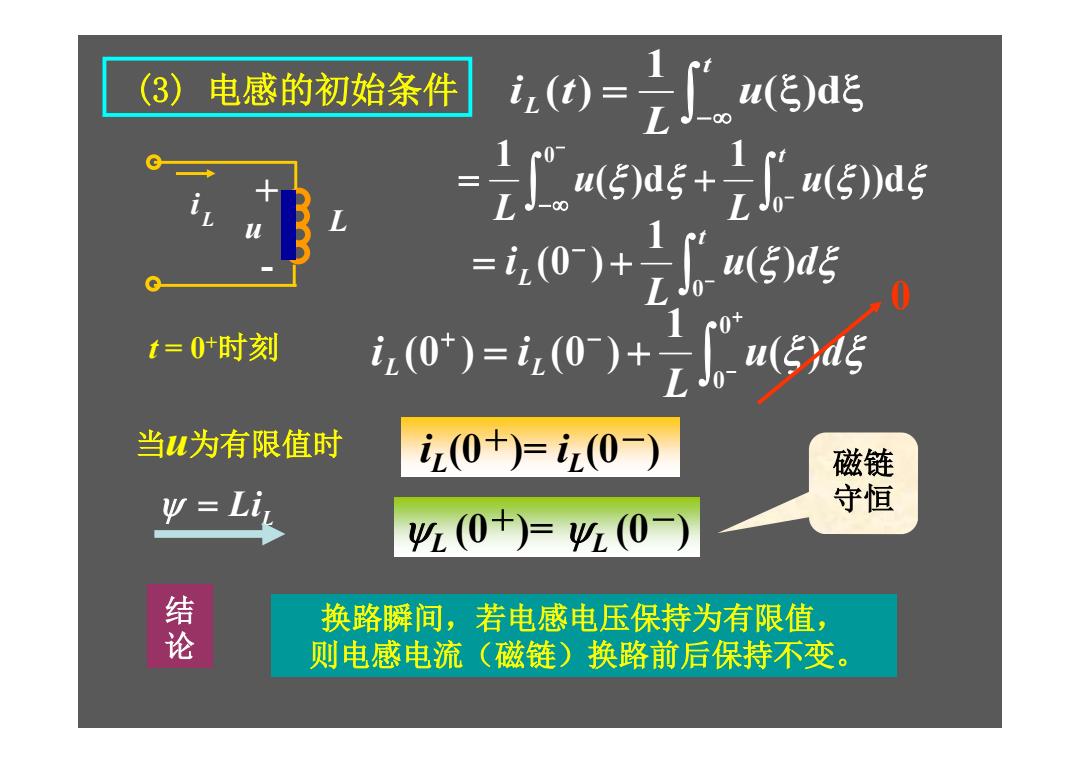
( )d 1 ( ) t L u L i t ( ))d 1 ( )d 1 0 0 t u L u L u d L i i L L ( ) 1 (0 ) (0 ) 0 0 当u为有限值时 L (0+)= L (0-) iL (0+)= iL (0-) i u L + - L (3) 电感的初始条件 t = 0+ 时刻 0 u d L i t L ( ) 1 (0 ) 0 LiL 磁链 守恒 换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。 结 论

(4)换路定律 「9e(0)=qe(0-) 换路瞬间,若电容电流保持为有限值, uc(0)=uc(0-)则电容电压(电荷)换路前后保持不变。 4(0)=4(0-) 换路瞬间,若电感电压保持为有限值, 0)=i0-) 则电感电流(磁链)换路前后保持不变。 注意: (1)电容电流和电感电压为有限值是换路定律成立的条件。 (2)换路定律反映了能量不能跃变
L (0+ )= L (0-) iL (0+ )= iL (0-) qc (0+ ) = qc (0-) uC (0+ ) = uC (0-) (4)换路定律 (1)电容电流和电感电压为有限值是换路定律成立的条件。 注意: 换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。 换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。 (2)换路定律反映了能量不能跃变
5.电路初始值的确定 (1)由0二电路求u(0)或i(0-) 例1求0) 10k 40k i10k 电容开路 40k wc(0-)=8V 10 2) 由换路定律 uc(0)=uc(0-)=8V 10k (3)由0+等效电路求0) 10V ic 2(0*)=10 0-8 0 -0.2m4 0+等效电路 电容用电 c(0-)=0+ic0) 压源替代
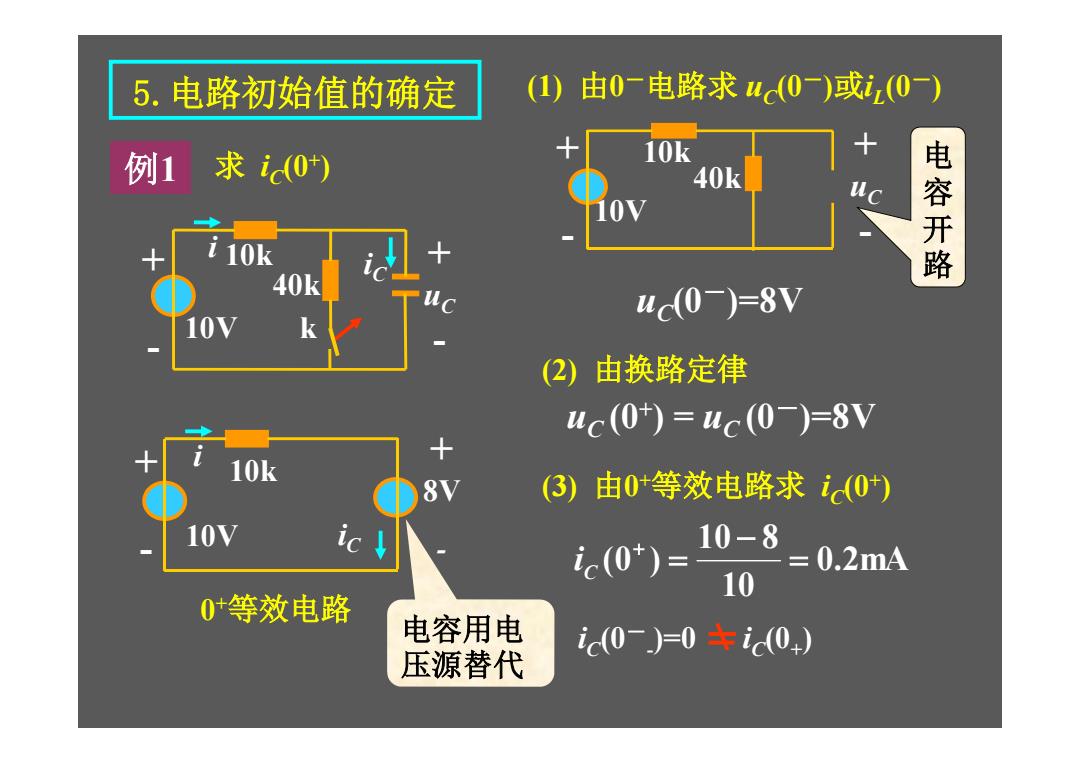
5.电路初始值的确定 (2) 由换路定律 uC (0+ ) = uC (0-)=8V + - 10V i iC + 8V - 10k 0+ 等效电路 0.2mA 10 10 8 (0 ) C i (1) 由0 -电路求 uC (0-)或iL (0-) + - 10V + uC - 10k 40k uC (0-)=8V (3) 由0+ 等效电路求 iC (0+ ) iC (0-- )=0 iC (0+ ) 例1 求 iC (0+ ) + - 10V i iC + uC - k 10k 40k 电 容 开 路 电容用电 压源替代