结论: (1)描述动态电路的电路方程为微分方程; (2)动态电路方程的阶数等于电路中动态元件的个数; 阶电路 阶电路中只有一个动态元件,描述 电路的方程是一阶线性微分方程。 dx +ax=e(t)t≥0 dt 二阶电路 二阶电路中有二个动态元件,描述电 路的方程是二阶线性微分方程。 d-x x dax=e(t) t≥0
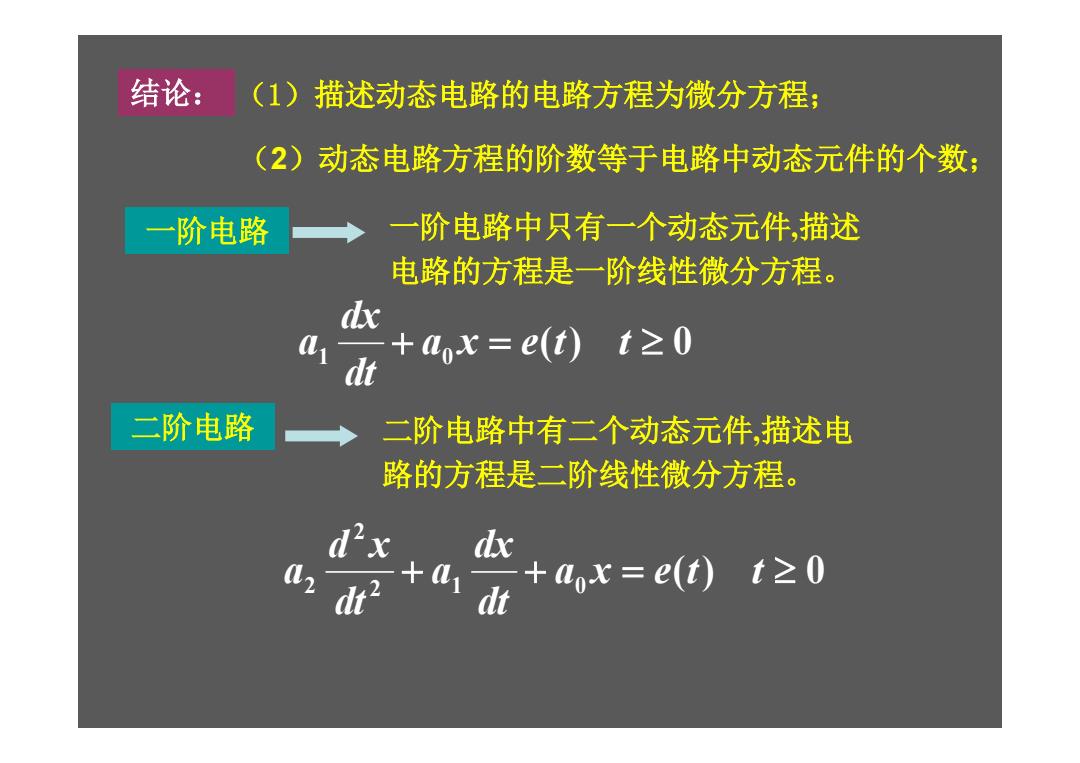
一阶电路 一阶电路中只有一个动态元件,描述 电路的方程是一阶线性微分方程。 结论: (1)描述动态电路的电路方程为微分方程; (2)动态电路方程的阶数等于电路中动态元件的个数; ( ) 0 1 a0 x e t t dt dx a ( ) 0 2 1 0 2 2 a x e t t dt dx a dt d x a 二阶电路 二阶电路中有二个动态元件,描述电 路的方程是二阶线性微分方程

高阶电路 电路中有多个动态元件,描述电路 的方程是高阶微分方程。 d"x d"-x c dt" +m-1 taditax=e()120 动态电路的分析方法 (1)根据K、KCL和VCR建立微分方程
高阶电路 电路中有多个动态元件,描述电路 的方程是高阶微分方程。 ( ) 0 1 1 0 1 1 a x e t t dt dx a dt d x a dt d x a n n n n n n 动态电路的分析方法 (1)根据KVl、KCL和VCR建立微分方程
(2)求解微分方程 时域分析法 复频域分析法 本章 采用 经典法 拉普拉斯变换法 状态变量法 卷积积分 状态变量法 付氏变换 数值法 工程中高阶微分方程应用计算机辅助分析求解
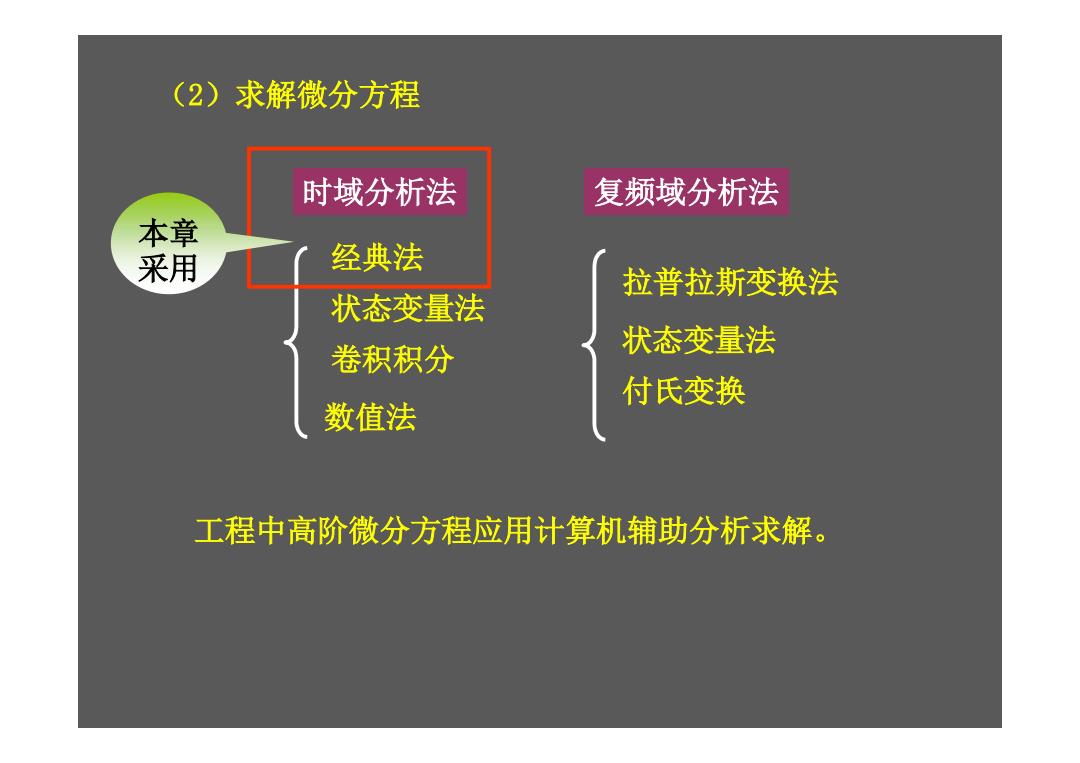
时域分析法 复频域分析法 (2)求解微分方程 经典法 状态变量法 数值法 卷积积分 拉普拉斯变换法 状态变量法 付氏变换 本章 采用 工程中高阶微分方程应用计算机辅助分析求解
稳态分析和动态分析的区别 稳态 动态 恒定或周期性激励 任意激励 换路发生很长时间后状态 换路发生后的整个过程 微分方程的特解 微分方程的一般解 x +aox=Us dt 00x=U
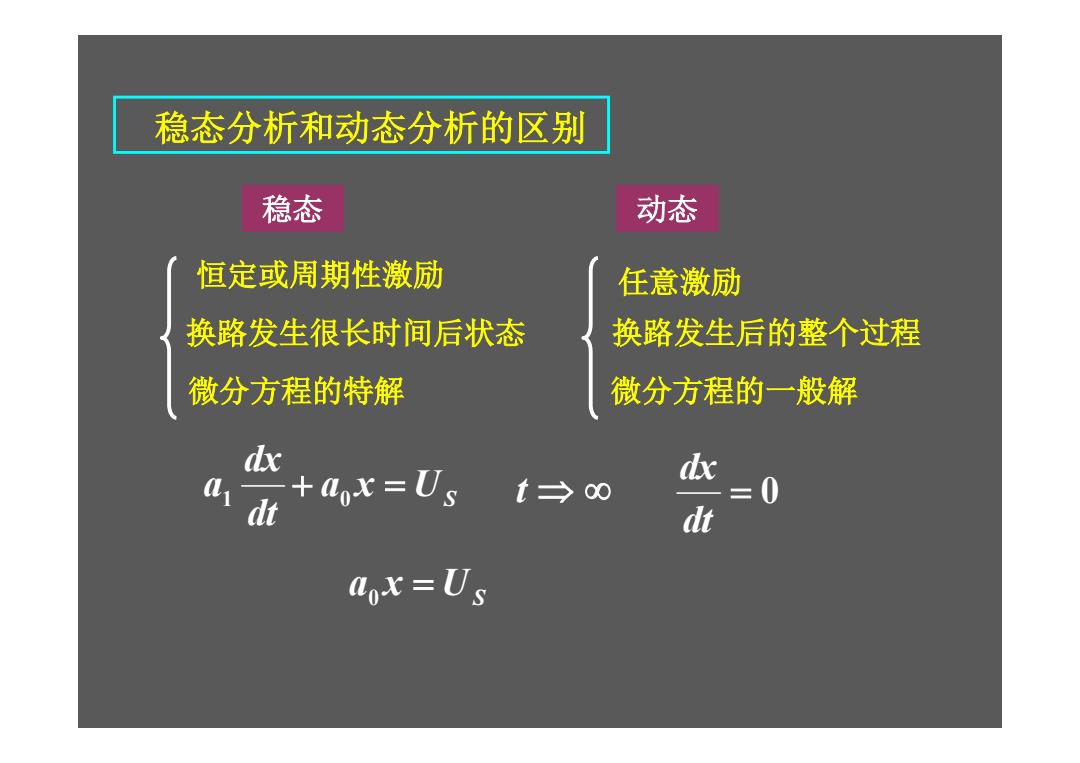
稳态分析和动态分析的区别 稳态 动态 换路发生很长时间后状态 微分方程的特解 恒定或周期性激励 换路发生后的整个过程 微分方程的一般解 任意激励 US a x dt dx a1 0 0 dt dx t US a0 x

3.电路的初始条件 f(0)=f(0* (1)t=0+与t=0一的概念 f(0)≠f(0*) 认为换路在仁0时刻进行 0- 换路前一瞬间 0-00+ 0+ 换路后一瞬间 f()=lim f(t) f(0*)=lim f(t) 0 t-→0 t>0 t<0 初始条件为t=0+时u,i及其各阶导数的值
(1) t = 0+与t = 0-的概念 认为换路在 t=0时刻进行 0 - 换路前一瞬间 0 + 换路后一瞬间 3. 电路的初始条件 (0 ) lim ( ) 0 0 f f t t t (0 ) lim ( ) 0 0 f f t t t 初始条件为 t = 0+时u ,i 及其各阶导数的值 0 -0 0 + t f(t) (0 ) (0 ) f f (0 ) (0 ) f f