
例如,以1978-2006年的数据为样本,以GDP作 为解释变量,建立居民消费函数。根据分析, 1992年前后,自发消费和消费率都可能发生变 化。 92年前 92年及以后 C=Bo+B GDP+B2 D +Bs (D GDP)+ t=1978,.,2006 通过统计检验,判断两个时期中消费函数的截 距和斜率是否发生变化
• 例如,以1978-2006年的数据为样本,以GDP作 为解释变量,建立居民消费函数。根据分析, 1992年前后,自发消费和消费率都可能发生变 化。 = 年及以后 年前 0 92 1 92 Dt 通过统计检验,判断两个时期中消费函数的截 距和斜率是否发生变化。 1978, ,2006 ( ) 0 1 2 3 = = + + + + t Ct GDPt Dt Dt GDPt t

三、虚拟变量的设置原则
三、虚拟变量的设置原则

每一定性变量(qualitative variable)所需的虚拟 变量个数要比该定性变量的状态类别数 (categories)少1。即如果有m种状态,只在模型 中引入m-1个虚拟变量。 。1 例如,季节定性变量有春、夏、秋、冬4种状 态,只需要设置3个虚变量: 春季 夏季 1 D 其它 其它 D,= 秋季 0 其它 如果设置第4个虚变量,则出现“虚拟变量陷井” (Dummy Variable Trap),为什么?
• 每一定性变量(qualitative variable)所需的虚拟 变量个数要比该定性变量的状态类别数 (categories)少1。即如果有m种状态,只在模型 中引入m-1个虚拟变量。 • 例如,季节定性变量有春、夏、秋、冬4种状 态,只需要设置3个虚变量: = = = 其它 秋季 其它 夏季 其它 春季 0 1 0 1 0 1 D1 D2 D3 如果设置第4个虚变量,则出现“虚拟变量陷井” (Dummy Variable Trap),为什么?
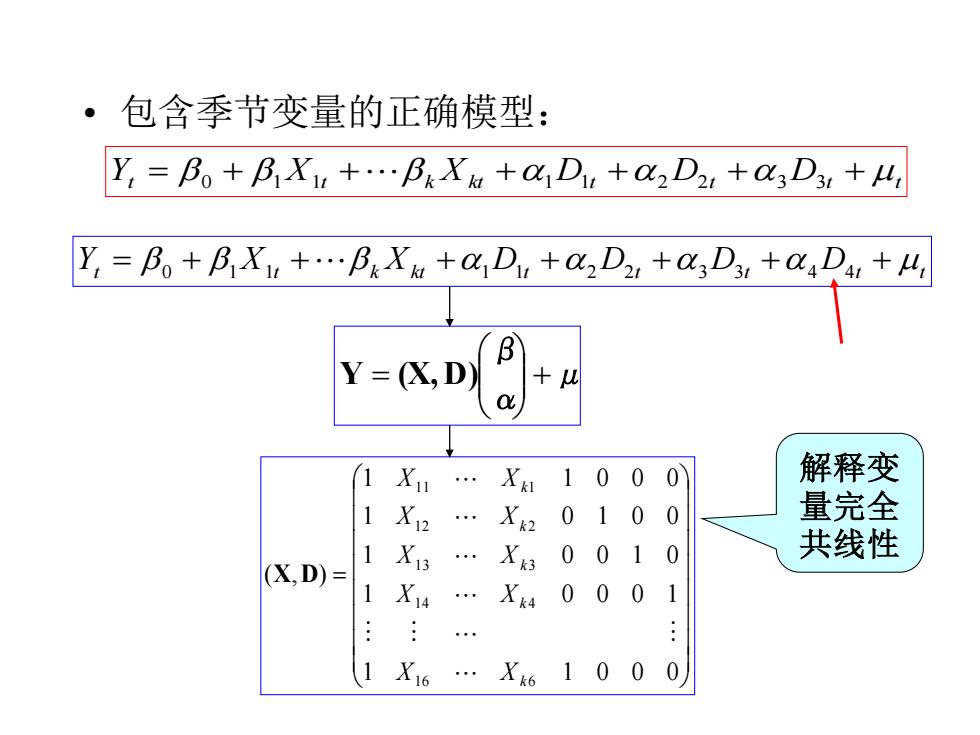
·包含季节变量的正确模型: Y,=阝o+B1Xi+.BkXa+aD+C2D2,+a3D3+4, Y,=B。+B,Xu+.PkXa+axD+a2D2+C3D3,+C4D4+4, B Y=(X,D) + 1 X1 100 0 解释变 1X2 . X2 0100 量完全 1 . 0010 共线性 (X,D)= X13 Xk3 1 X14 X40001 : X6.X6100 0
• 包含季节变量的正确模型: Yt = 0 + 1 X1t + k Xkt +1 D1t + 2 D2t +3 D3t + t Yt = 0 + 1 X1t + k Xkt +1 D1t + 2 D2t +3 D3t + 4 D4t + t μ α β Y (X, D) + = = 1 1 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1 0 0 0 ( , ) 1 6 6 1 4 4 1 3 3 1 2 2 1 1 1 k k k k k X X X X X X X X X X X D 解释变 量完全 共线性

● 如果在服装需求函数模型中必须包含3个定性 变量:季节(4种状态)、性别(2种状态)、 职业(5种状态),应该设置多少虚变量? 一模型含常数项 一模型不含常数项
• 如果在服装需求函数模型中必须包含3个定性 变量:季节(4种状态)、性别(2种状态)、 职业(5种状态),应该设置多少虚变量? – 模型含常数项 – 模型不含常数项