西安电子科技大学：《数字信号处理》课程教学课件（讲稿）02 时域离散信号和系统的频域分析（1/2）

得： sink π sin k IX()= j 2 2 sin sin- 8 8 序列 幅频特性 1.5 4 0.5 10 10 周期信号的频谱是离散线状谱 信号的周期为N,则X(k)的周期为N。 23

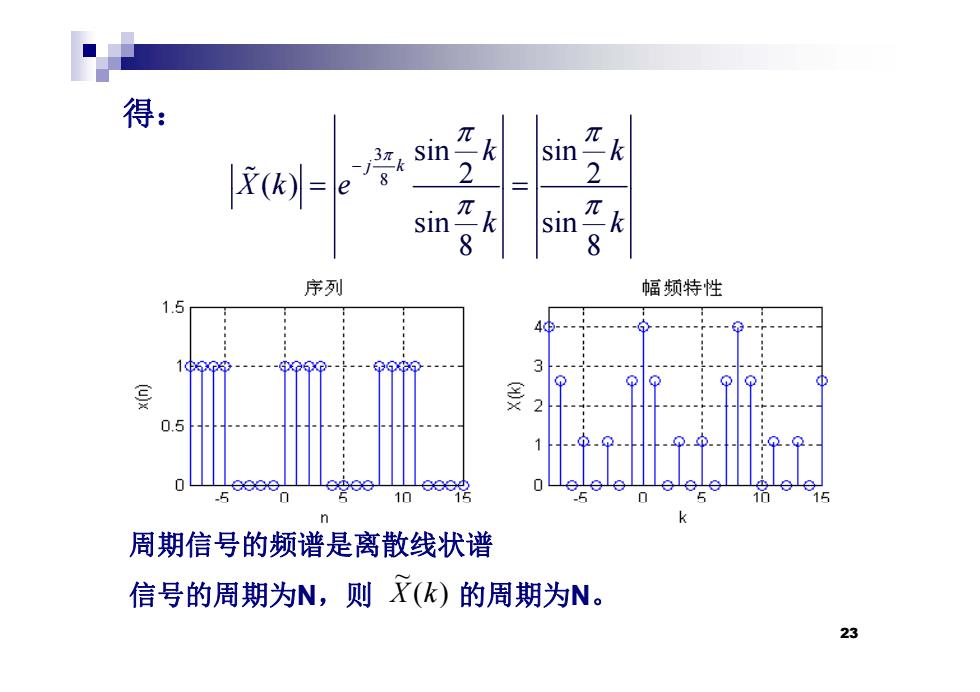
得： 3 8 sin sin 2 2 ( ) j k k k Xk e      ( )   sin sin 8 8 Xk e k k     周期信号的频谱是离散线状谱 ~ 23 信号的周期为N，则 的周期为 X (k) N

2.2.3周期信号的傅里叶变换 ■序列的傅立叶变换的条件是序列必须绝对可和， 某些序列不满足绝对可和的条件，因此严格讲傅 立叶变换不存在。 ■但如果像连续信号那样，引入奇异函数（单位冲 激函数)，傅立叶变换的定义可以放松，可以用 冲激函数表示其傅立叶变换。 24

223 . . 周期信号的傅里叶变换 周期信号的傅里叶变换  序列的傅立叶变换的条件是序列必须绝对可和， 某些序列不满足绝对可和的条件，因此严格讲傅 立叶变换不存在。  但如果像连续信号那样，引入奇异函数（单位冲 激函数），傅立叶变换的定义可以放松，可以用 冲激函数表示其傅 冲激函数表示其傅 叶变换 立 。 24

复指数序列的傅里叶变换 ■复指数序列的傅里叶变换 口x()=ew的傅里叶变换 FT(①)）=2π6(2) X(j2)=FT(eo)=2π6(2-2) 口假设复指数序列eo”的傅里叶变换为 Xer)=FT(ew)=∑2m(o-o-2rr） -元≤0。≤π 25

复指数序列的傅里叶变换  复指数序列的傅里叶变换  xt e a ( )  j 0t 的傅里叶变换 j  FT(1) 2 ( )     假设复指数序列 的傅里叶变换为 0 0 ( ) ( )2 ( ) j t X j FT e a       0 j n e  0 0 ( ) ( ) 2( 2) j j n X e FT e r          r  25

复指数序列的傅里叶变换 X(e)=FT(ea")=∑2δ(o-0-2πr)） =-00 ■是以2π为周期的单位脉冲序列 ■上式为假设，如该假设成立，其傅立叶反变换应为 IFT[X(el0)]=ejoo 26

复指数序列的傅里叶变换 0 0 ( ) ( ) 2( 2) j j n r X e FT e r              是以 为周期的单位脉冲序列 r    2   上式为假设，如该假设成立，其傅立叶反变换应为 0 [ ( )] j j n IFT X e e    26

X(em)=FT(ea")=∑2π6(o-0,-2πr） “0 ■求证：IFT[X(eo)]=eon I.Xee-do 2m(rdo 2rto-@omdo -cma 27

0 ( ) ( ) 2( 2) j j n X FT      求 [ ( )] j j n  0 0 ( ) ( ) 2( 2) j j n r X e FT e r            求证： 0 [ ( )] j j n IFT X e e    1 ( ) 2 j jn Xe e d        0 1 2( 2) 2 j n re d               2 r     1 0 0 2( ) 2 j n j n ed e              27