西安电子科技大学：《数字信号处理》课程教学课件（讲稿）02 时域离散信号和系统的频域分析（1/2）

般周期序列的傅里叶变换 ■设()为以N为周期的周期序列，则可展成傅里叶级数 (m)e -00<n<0 N ■对每一项进行傅立叶变换 X(e)=FT(e)=>278(0-0-2xr) r}re学2aa 2πk-2πr） (e)=FT[sok2) 28

一般周期序列的傅里叶变换  设 ( ) 为 以 N为 期的 期序 为 周期的 周期序列，则 傅叶数 可展成 傅 里 叶 级 数 1 2 1 () () N j kn N X k      x( ) n 对每 项进行傅立叶变换 0 1 () () j N k x n X k e n N       0 ( ) ( ) 2( 2) j j n X FT       对每 一项进行傅立叶变换  2 12 2 () () ( 2 ) j kn N FT X k e X k k r                0 0 ( ) ( ) 2( 2) j j n r X e FT e r            () () ( 2 ) r FT X k e X k k r NN N           1 2 2 N    1 0 2 2 ( ) () () ( 2 ) N j k r X e FT x n X k k r N N                  28

般周期序列的傅里叶变换 e=ma2器2ao-2am 由于： k=0,1,2,.,N-1 r=.,-2,-1,0,1,2,., 于是： xe")-Frso- 2利 。周期序列的傅里叶变换由0=2亚k,-0<k<0的冲激函 数的和组成，各冲激函数的强度为)，（似）是离散 傅里叶级数的系数。 29

一般周期序列的傅里叶变换   1 2 2 ( ) () () ( 2 ) N j X e FT x n X k k r               0 ( ) () () ( 2 ) k r X e FT x n X k k r N N          由于： k N  012 1 , , 2, , 1 , 2, 1,0,1, 2, , k N r        由于：   2 2 ( ) () ()( ) j X e FT x n X k k N N           于是：  N N k  周期序列的傅里叶变换由 的冲激函 2 k k   周期序列的傅里叶变换由     的冲激函 数的和组成，各冲激函数的强度为 ， 是离散 k k , N     2 X k( ) N  X k( )  29 傅里叶级数的系数

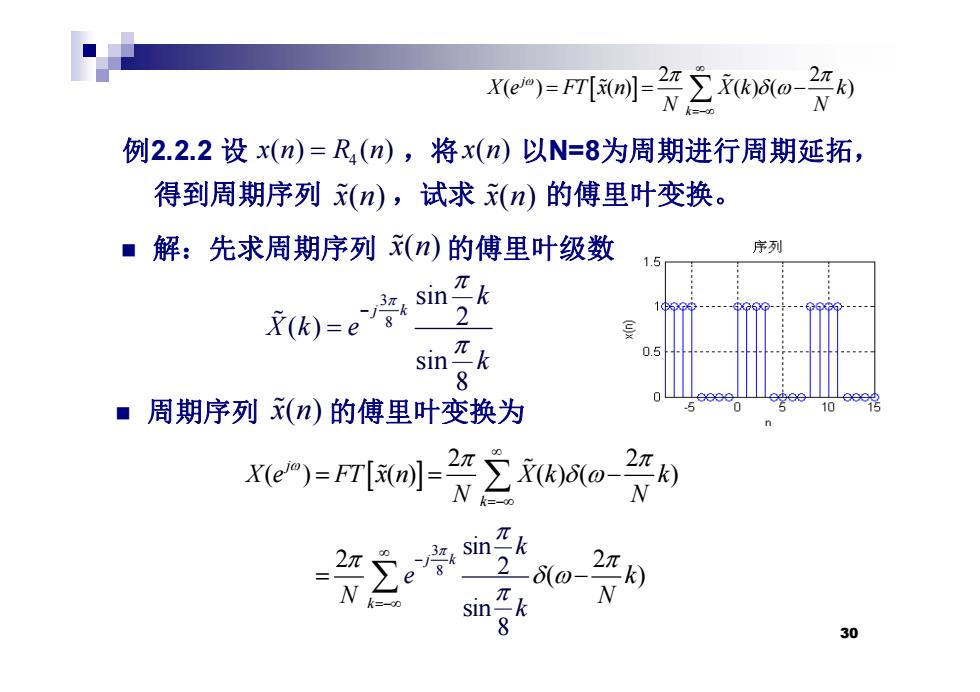
e=Fm[=2o 例2.2.2设x(n)=R(n),将x(n以N=8为周期进行周期延拓， 得到周期序列x(n),试求(n)的傅里叶变换。 ■解：先求周期序列(n)的傅里叶级数 序列 si 3π， X(k)=e 8 2 sink 0.5 ■周期序列x(n)的傅里叶变换为 5 0 10 2-60 π sin二k 8 30

  2 2 ( ) () ()( ) j k X e FT x n X k k N N              例2.2.2 设 ，将 以N=8为周期进行周期延拓， 得到周期序列 试求 的傅里叶变换 4 xn R n () ()  x( ) n ( ) ( ) N N k 得到周期序列 x( ) n ，试求 x( ) n 的傅里叶变换。  解：先求周期序列 的傅里叶级数 x( ) n 3 8 sin 2 ( ) j k k Xk e       sin 8 k   周期序列 的傅里叶变换为 x( ) n   2 2 ( ) () ()( ) j k X e FT x n X k k N N             ( ) 3 8 sin 2 ( 2 2 ) k j k k k e              30 si ( n ) 8 k k N N e k     

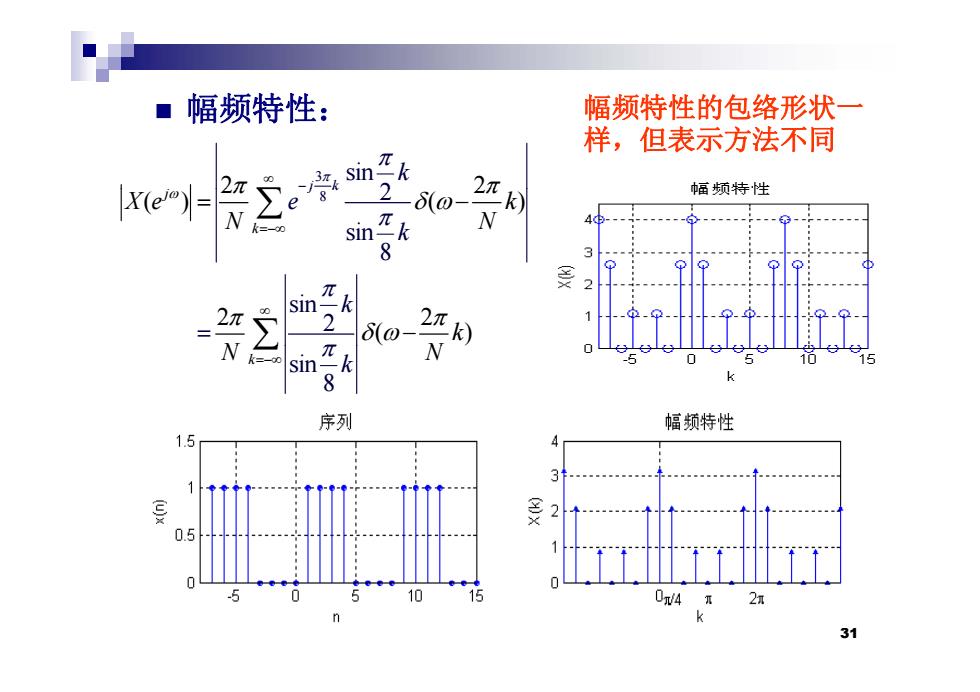
幅频特性： 幅频特性的包络形状一 样，但表示方法不同 3k si [X(e)|= 260- 幅频特性 e N sink N sin =2 2 6(0- ) N sin 5 1 15 8 序列 幅频特性 1.5 2 0.5 10 04 27 31

 幅频特性 ： 幅频特性的包络形状 一 3 2 2 sin j 2 j k  k       幅频特性的包络形状 样，但表示方法不同 8 2 2 () ( ) 2 sin 8 j j k k X e k N N e k           sin 2 2 2 ( ) k k N N           si 8 n k k N N    31

■ 例2.2.4令(n)=coso,n,2π/o为有理数，求其傅里叶 变换。 ■解： FT[ea"]=∑2π(o-o-2πr) FTIR(n)]=FTle+e-] -222m8w-2rj+2o+ou-2r1 =π∑[6(0-0-2πr）+80+0,-2r)] 32

 例224 . . 令 xn n ( ) cos   ，2 /   为有理数，求其傅里叶 变换。 0 xn n ( ) cos   0 2 /    解： 0 0 1 () ( ) 2 j n j n xn e e       2 0 0 [ ] 2( 2) j n FTe r         r 0 0 1 [ ( )] [ ] jn jn FT x n FT e e    [ ( )] [ ]    2 1 [2 ( 2 ) 2 ( 2 )] FT x n FT e e         r r        0 0 [2 ( 2 ) 2 ( 2 )] 2 ( 2) ( 2) r         r r             32  ( 2) ( 2) 0 0  r    r r         