
2.2.1时域离散信号的傅里叶变换定义 ■连续信号的傅立叶变换 连续函数一 X(U2∫x)edt ■时域离散信号的傅立叶变换(DTFT) 正变换: X(eF∑xn)e 0=2T T是采样间隔 (注意:频谱是o的连续函数,以2π为周期) 成立条住 序列x(n)绝对可和,或者说序列能量有限,即 ∑xnl<o 12
221 . . 时域离散信号的傅里叶变换定义 时域离散信号的傅里叶变换定义 连续信号的傅立叶变换 j ( ) () t X j x t e dt 连续函数 - 时域离散信号的傅立叶变换 (DTFT) X j x t e dt ( ) () 连续函数 - 正变换: ( ) () j jn n X e xne T T是采样间隔 (注意:频谱是 的连续函数,以 为周期) 成立条件 2 序列 绝对可和,或者说序列能量有限,即 x n( ) 12 ( ) n x n

2.2.1时域离散信号的傅里叶变换定义 ■时域离散信号的傅立叶变换(DTFT) 反变换: xn)=,X(edo 2πJ-元 注意: 正变换求和区间为(-∞,0) 反变换积分区间仅为[-π,π] ■证明: o)=[区0eo 13
221 . . 时域离散信号的傅里叶变换定义 时域离散信号的傅里叶变换定义 时域离散信号的傅立叶变换(DTFT) 反变换: 1 () ( ) j jn xn X e e d 反变换: 注意: () ( ) 2 xn X e e d 正变换求和区间为 ( ,) 反变换积分区间仅为 [ ] 证明: [, ] 证明: 1 ( ) () 2 jl jn x n xle e d 13 2 l

a[区0ea -02∫do=立 sinπ(n-I) π(n-) 由于: sinπ(n-)_1n= π(n-1)0n≠ =6n-0 于是:-立0婴》-立0-小=n 证毕 14
1 ( ) () 2 jl jn l x n xle e d 2 l ( ) 1 j l j n x l e e d sin ( ) ( ) n x l l ( ) 2 l ( ( ) ) l n l 由于: sin ( ) 1 ( ) 0 n l n l n l n l ( ) n l 于是: ( ) sin ( ) ( ) () n l xn xl xl n l xn () ( ) ( ) 于是: 证毕 ( ) () l ( ) xn xl n l () ( ) ( ) l xl n l xn 14 证毕

2.2.1时域离散信号的傅里叶变换定义 ■总结:序列的离散时间傅立叶变换对 Xe)=∑xnem=K(eee ia∫en 幅频特性 X(e) 相频特性 arg[X(e月 ■注意: DTFT成立的条件、n取整数、DTFT是连续周期函数、 积分上下限 15
221 . . 时域离散信号的傅里叶变换定义 时域离散信号的傅里叶变换定义 总结:序列的离散时间傅立叶变换对 ( ) () j jn X arg[ ( )] ( ) j j j Xe X 1 j j ( ) () j jn n X e xne arg[ ( )] ( ) j j Xe X e e 1 () ( ) 2 j j n x n Xe e d 幅频特性 相频特性 ( ) j X e a gr [( )] j X e 注意: DTFT成立的条件 取整数 DTFT是连续周期函数 15 DTFT成立的条件、n取整数、DTFT是连续周期函数、 积分上下限
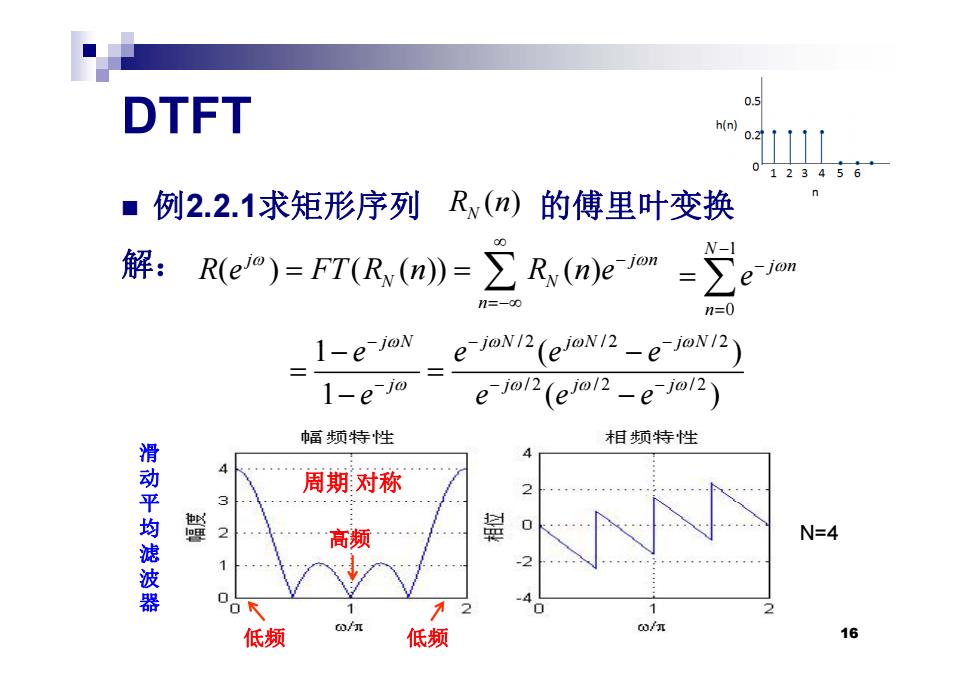
DTFT 0.5 h(n) 0.2 123456 ■例2.2.1求矩形序列Rv(n)的傅里叶变换 解:Re)=PR,m》=立R(mem=是 -jon n=0 1-e-joN e-jaN2(elov12-e-joN12) 1-e-jo e-jol2(ejol2 -e-jol2) 幅频特性 相频特性 滑动平均滤波器 周期对称 2 量 高频 N=4 1 A 低频 低频 16
DTFT 例2.2.1求矩形序列 的傅里叶变换 解: ( ) R n N ( ) ( ( )) ( ) j j n R e FT R n R n e N 1 j n 解: ( ) ( ( )) ( ) j j N N n R e FT R n R n e 0 j n n e /2 /2 /2 1 () jN jN jN jN /2 /2 /2 /2 /2 /2 1 () 1 () jN jN jN jN j jj j e ee e e ee e 滑 动 平 周期 对称 均 N=4 滤 波 高频 16 器 低频 低频