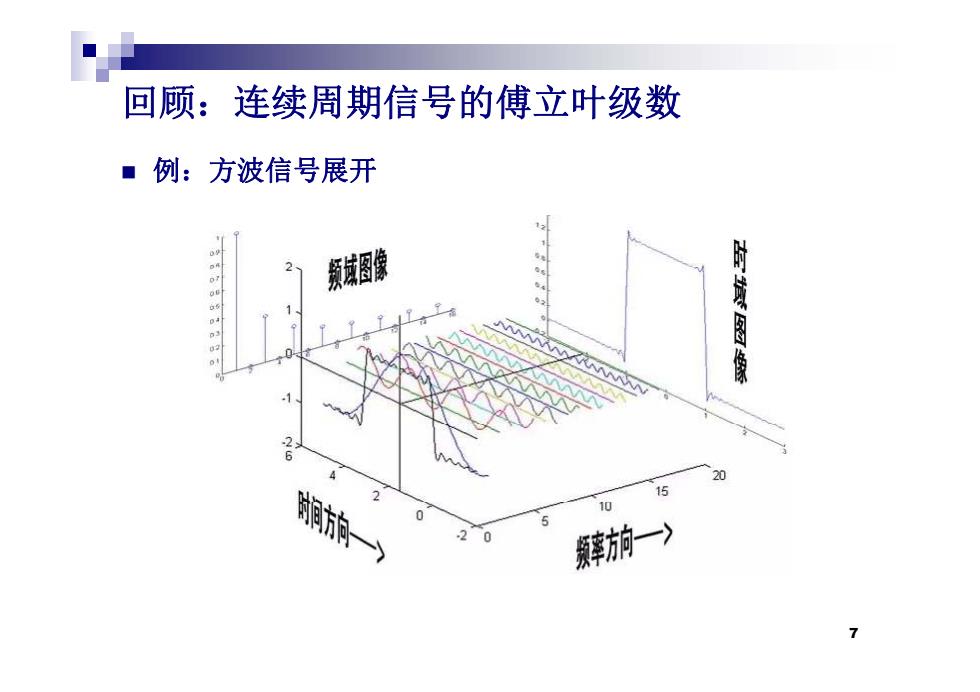
回顾:连续周期信号的傅立叶级数 ■例:方波信号展开 豫 时诚图 像 15 10 摩前一〉 7
回顾:连续周期信号的傅立叶级数 例:方波信号展开 7

回顾:连续周期信号的傅立叶级数 https://en.wikipedia.org/wiki/Fourier series Function s(x)(in red)is a sum of six sine functions of different amplitudes and harmonically related frequencies.Their summation is called a Fourier series The Fourier transform,S(f) (in blue),which depicts amplitude vs frequency, reveals the 6 frequencies (at odd harmonics)and their amplitudes(1/odd number). ·推荐:[知乎]傅里叶分析之掐死教程(完整版)https:zhuanlan.zhihu.comp/19763358
回顾:连续周期信号的傅立叶级数 https://en.wikipedia.org/wiki/Fourier_series Function s(x) (in red) is a sum of six sine functions of different amplitudes and harmonically related frequencies. Their summation is called a Fourier series. The Fourier transform, S(f) (in blue), which depicts amplitude vs frequency, reveals the 6 frequencies (at odd harmonics) and their amplitudes (1/odd number). 8 • 推荐:[知乎] 傅里叶分析之掐死教程(完整版) https://zhuanlan.zhihu.com/p/19763358
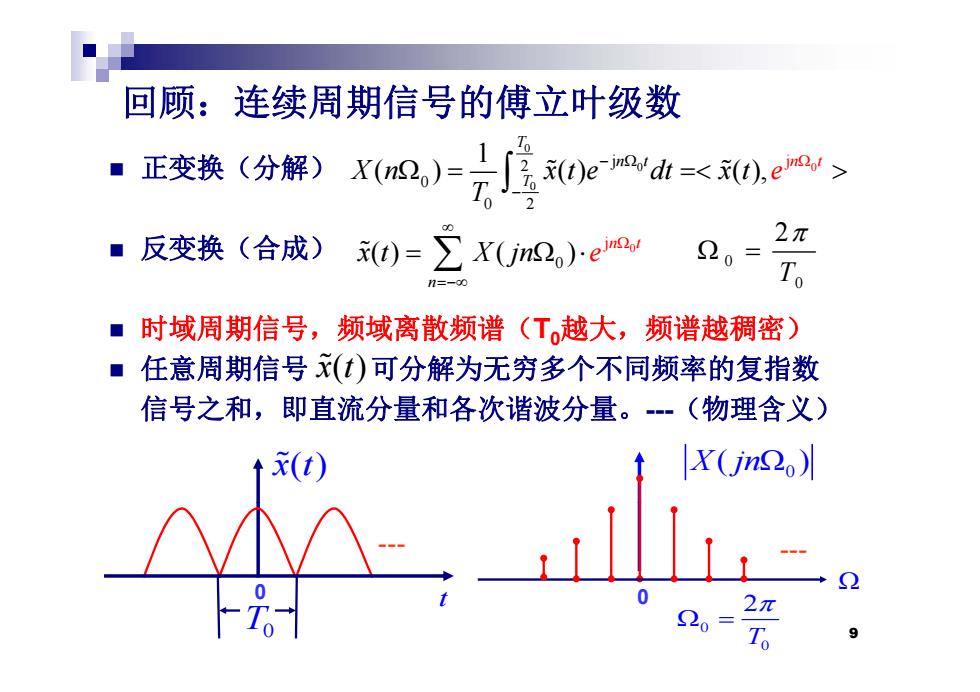
回顾:连续周期信号的傅立叶级数 ·正变换(分解)Xu2,)=值0ead=<0.e> ■反变换(合成) 0)=∑X(Um2)ee 20= 2π To ■时域周期信号,频域离散频谱(T越大,频谱越稠密) ■任意周期信号x()可分解为无穷多个不同频率的复指数 信号之和,即直流分量和各次谐波分量。·(物理含义) x(t) 0 -To 2π 9
回顾:连续周期信号的傅立叶级数 正变换(分解) 0 0 0 0 j j 2 0 1 ( ) ( ) ( ), T n t n T t X n x t e dt t x e T 反变换(合成) 0 2T 0 0 j () ( ) n t x t jn X e 0 0 2 T 时域周期信号,频域离散频谱(T0越大,频谱越稠密) T0 0 n 任意周期信号 可分解为无穷多个不同频率的复指数 信号之和,即直流分量和各次谐波分量。-(物理含义) x t ( ) 0 x ( )t X jn ( ) - - 9 0 0 2 T T0 t 0 0
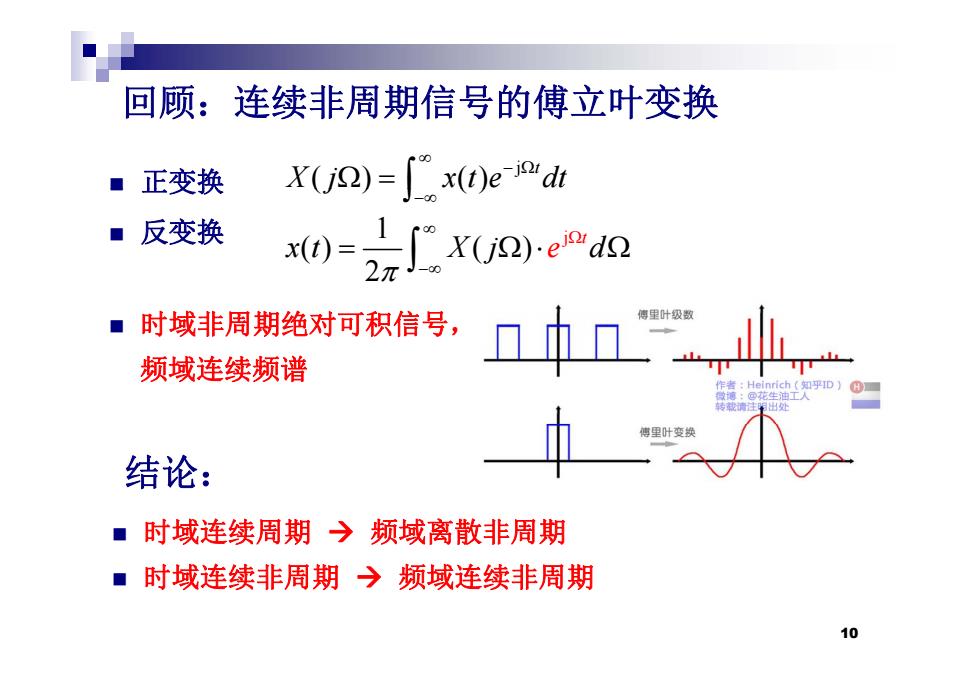
回顾:连续非周期信号的傅立叶变换 ■正变换 X(j)=[x(t)edr ■反变换 x0=是∫x(U2-ed2 2π ■ 时域非周期绝对可积信号, 里叶级 巾口 频域连续频谱 H 博里叶变换 结论: ■时域连续周期→频域离散非周期 ■时域连续非周期→频域连续非周期 10
回顾:连续非周期信号的傅立叶变换 正变换 j ( ) () t X j x t e dt 正变换 反变换 1 j () ( ) 2 t x t X j d e ( ) () j 时域非周期绝对可积信号, 2 频域连续频谱 结论: 时域连续周期 频域离散非周期 时域连续非周期 频域连续非周期 10

2.2时域离散信号的傅里叶变换 ■时域离散信号的傅里叶变换(DTFT)的定义 ■周期信号的离散傅里叶级数(DFS) ■周期信号的傅里叶变换 ■时域离散信号傅里叶变换的性质
2 2. 时域离散信号的傅里叶变换 时域离散信号的傅里叶变换(DTFT)的定义 周期信号的离散傅里叶级数(DFS) 周期信号的傅里叶变换 时域离散信号傅里叶变换的性质 11