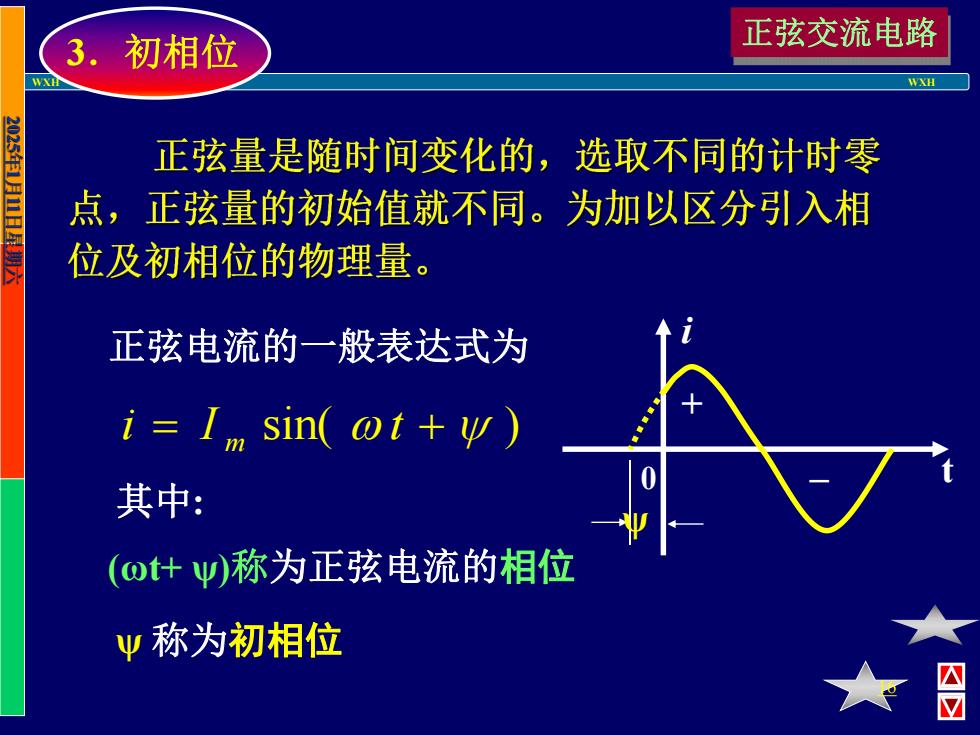
3.初相位 正弦交流电路 WXH 202S6E1 正弦量是随时间变化的,选取不同的计时零 点,正弦量的初始值就不同。为加以区分引入相 位及初相位的物理量。 正弦电流的一般表达式为 i=I,sin(ot+y 其中: (o+y称为正弦电流的相位 业称为初相位
WXH WXH 16 3.初相位 i I sin( t ) m 正弦电流的一般表达式为 其中: 0 i t + _ (ωt+ ψ)称为正弦电流的相位 ψ 称为初相位 ψ 正弦交流电路
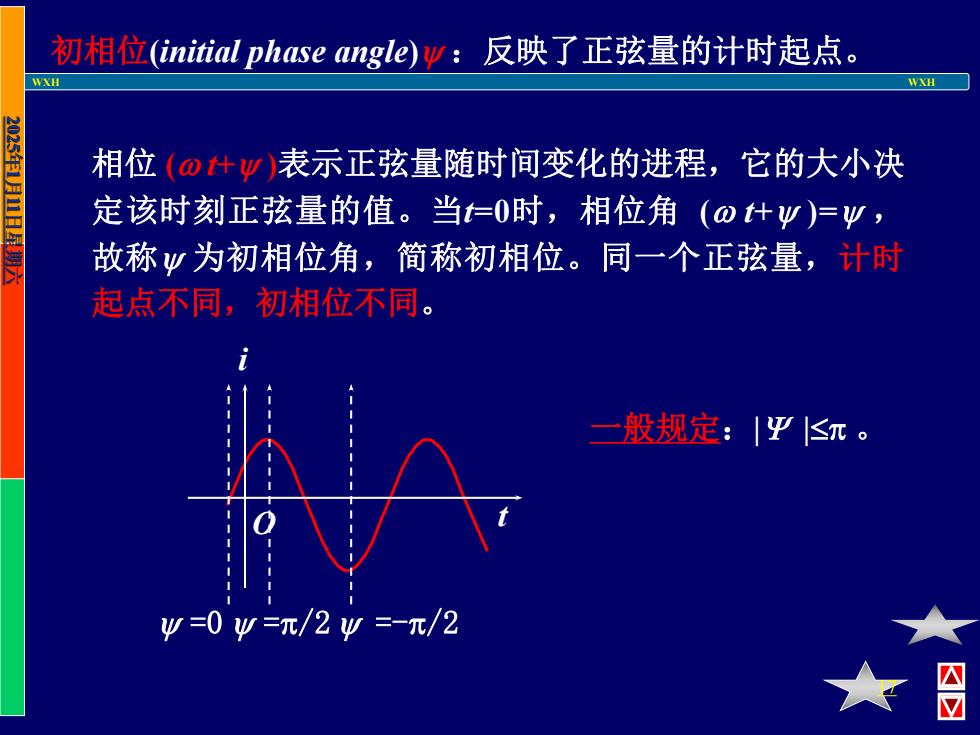
初相位(initial phase angle)y:反映了正弦量的计时起点。 WXH 相位(@体Ψ)表示正弦量随时间变化的进程,它的大小决 定该时刻正弦量的值。当仁0时,相位角(o什y)=必, 故称必为初相位角,简称初相位。同一个正弦量,计时 起点不同,初相位不同。 般规定:」平≤π。 w=0W=π/2Ψ=-元/2
WXH WXH 17 初相位(initial phase angle) :反映了正弦量的计时起点。 相位 ( t+ )表示正弦量随时间变化的进程,它的大小决 定该时刻正弦量的值。当t=0时,相位角 ( t+ )= , 故称 为初相位角,简称初相位。同一个正弦量,计时 起点不同,初相位不同。 t i O =0 =/2 =-/2 一般规定:| |
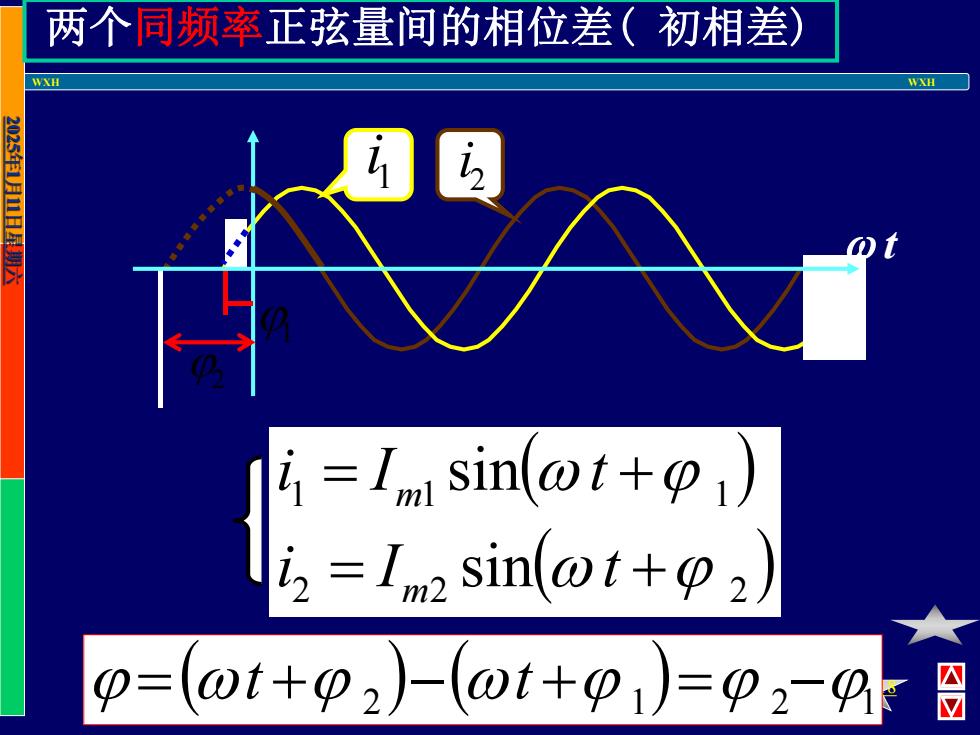
两个同频率正弦量间的相位差(初相差 i=Im sinot+) i,=Im2sin(ot+p2) p=(@t+p2)-(@t+o1)=P2-O: 四区
WXH WXH 18 2 1 21 t t 两个同频率正弦量间的相位差( 初相差) 2 2 2 1 1 1 sin sin i I t i I t m m 1 2 2 i 1 i t

正弦交流电路 WXH h=Um sin(ot+平i)i三Im sin(ot+Ψ2) 定义p=(1-2)为相位差或初相差。 当p=(1-2)>0时,称u比i超前φ 角0=(中1- 2)<0时,称u比i滞后p角; 当φ=(1-2)=0时,称1与i同相。 当φ=(1- 业2)=90时,称u与i正交。 当φ=(业1-ψ2)=180°】 时,称u与i反相 (相位相反),或相差180° ()只有同频率的正弦量才能比较相位差 意 (2)φ的取值范围φ≤π 四区
WXH WXH 19 sin( ) 1 u U m t sin( ) 2 i I m t 当φ =(ψ1 – ψ2) 0 时,称 u 比 i 超前 φ 当角φ;=(ψ1 – ψ2) 0 时,称 u 比 i 滞后 φ 角; 当φ =(ψ1 – ψ2) =0 时,称 u 与 i 同相。 当φ =(ψ1 – ψ2) = 180° 时,称 u 与 i 反相 (相位相反),或相差180° 当φ =(ψ1 – ψ2) = 90 o时,称 u 与 i 正交。 注 意 正弦交流电路

可以证明同频率正弦波运算后,频率不变 X WXH u1=√2U1sin(wt+p1) 如: u2=V2U2sin(ot+p2) u=u1+2 =v2U sin(@t+)+v2U sin(@t+pz) =v2Usin(@t+p) 幅度、相位变化 频率不变 结论: 因角频率(⊙)不变,所以以下讨论同频率正弦波 时,⊙可不考虑,主要研究幅度与初相位的变化 四区
WXH WXH 20 可以证明同频率正弦波运算后,频率不变。 2 2 2 1 1 1 2 sin 2 sin u U t u U t 如: 结论: 因角频率()不变,所以以下讨论同频率正弦波 时, 可不考虑,主要研究幅度与初相位的变化。 U t U t U t u u u 2 sin 2 sin 2 sin 1 1 2 2 1 2 幅度、相位变化 频率不变