工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 平衡微分方程式 该方程对不可压缩流体和 可压缩流体的静止和相对 静止状态都适用,是流体 静力学的基本方程。 f 1 ap 二0 1p0 p ay 形式 f. 1 ap 0 压强梯度 pressure gradient 上式即为流体平衡微分方程,又称为欧拉平衡微分方程。 该式的物理意义为:在静止流体内的任一点上,作用在单位质量 流体上的质量力与静压强的合力相平衡
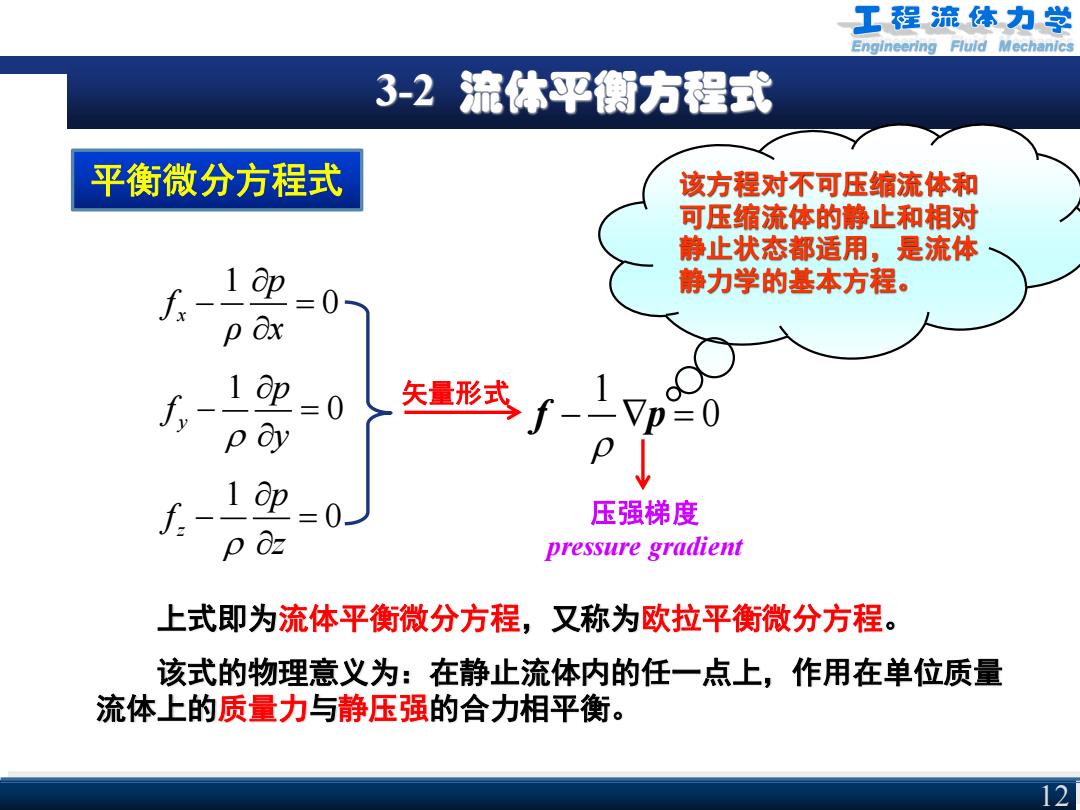
Engineering Fluid Mechanics 3-2 流体平衡方程式 平衡微分方程式 1 0 x p f ρ x − = 1 0 y p f y − = 1 0 z p f z − = 1 0 f p − = 矢量形式 上式即为流体平衡微分方程,又称为欧拉平衡微分方程。 该式的物理意义为:在静止流体内的任一点上,作用在单位质量 流体上的质量力与静压强的合力相平衡。 该方程对不可压缩流体和 可压缩流体的静止和相对 静止状态都适用,是流体 静力学的基本方程。 压强梯度 pressure gradient 12

工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 压强差公式 -2-0-12-0 -1迎=0 p ay 乘以dk、dy、dz,然后相加 p(fd+f,y+fd) op dx*oy opd也 op dy 流体静压强是空间坐标的连续函数,它的全微分为 dp op dx +op dy+ op dz 压强差公式,表明 8x Oy 流体静压强的增量 取决于单位质量力 故:dp=p(f+f,dy+fdb 和坐标增量。 3
Engineering Fluid Mechanics 3-2 流体平衡方程式 压强差公式 1 0 x p f ρ x − = 1 0 y p f y − = 1 0 z p f z − = 乘以dx、dy、dz,然后相加 ( x y z ) p p p f dx f dy f dz dx dy dz x y z + + = + + dp f dx f dy f dz = + + ( x y z ) 流体静压强是空间坐标的连续函数,它的全微分为 z z p y y p x x p dp d d d + + = 故: 压强差公式,表明 流体静压强的增量 取决于单位质量力 和坐标增量。 13

工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 等压面 在流场中压强相等的点组成的面 dp=0或pk=c0st dp=p(fd+f,dy+fb)=0→fk+,+f=0 形式 f.dr=0 等压面的微分方程,表明在静 止的流体中作用于任一点的质 量力垂直于经过该点的等压面。 4
Engineering Fluid Mechanics 3-2 流体平衡方程式 等压面 ( ) 0 x y z dp f dx f dy f dz = + + = 在流场中压强相等的点组成的面 dp=0 或 p(x,y,z)=const 0 x y z f dx f dy f dz + + = 矢量 形式 f dr = 0 等压面的微分方程,表明在静 止的流体中作用于任一点的质 量力垂直于经过该点的等压面。 14

工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 平衡条件 势函数 对于不可压缩流体,p=常数 dp=p(fdxtfdyifdz)>d(plp)fdx+fdy+fdz 个 全微分 必须是全微分 右边成为某一个函数全微分的必要且充分的条件是 f,- =0 f:_f=0 f_f-0 02 Oy 8x 0z 设用-π(x,y,z)代表这一函数,则 若要使不可压缩流体处于平衡 O 0π 状态,则作用在它上面的质量 x 1.= Oπ 力必须有势,-π(x,y,) 82 就是质量力的势函数 5
Engineering Fluid Mechanics 3-2 流体平衡方程式 平衡条件 势函数 对于不可压缩流体, = 常数 dp= (fxdx+fydy+fzdz) d(p/)=fxdx + fy dy + fz dz 全微分 右边成为某一个函数全微分的必要且充分的条件是 = 0 y f z f y z - = 0 z f x f z x - 0 z y f f y z − = 设用−(x,y,z)代表这一函数,则 x f x = − y f y = − z f z = − 若要使不可压缩流体处于平衡 状态,则作用在它上面的质量 力必须有势,−(x,y,z) 就是质量力的势函数 必须是全微分 15

工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 平衡条件 势函数 等势面:势函数相等的诸点组成的面,有势函数存在的质量力称为有势力 dp=p(fdc+f,y+f正) 积分 取积分常数为零 0π f.-Ox 0兀 ∫y=- π=-plp f.=- 8v 8z 质量力不仅垂直于等压面, 而且指向压强增大的方向 f=-Vπ=-gradπ a 1→ = i+ 8x 对于流体的密度只随压强变化的正压流场,即等密度面与等压面平行的流场 可将压强差公式写成d∫他-f,d+,+fd 0 同样可证明:若要使正压流场中的流体处于平衡状态,则作用在它上面的 质量力必须有势 6
Engineering Fluid Mechanics 3-2 流体平衡方程式 平衡条件 势函数 等势面:势函数相等的诸点组成的面,有势函数存在的质量力称为有势力 =−p/ρ 质量力不仅垂直于等压面, 而且指向压强增大的方向 对于流体的密度只随压强变化的正压流场,即等密度面与等压面平行的流场 可将压强差公式写成 = f x + f y + f z ρ p x y z d d d d d 同样可证明:若要使正压流场中的流体处于平衡状态,则作用在它上面的 质量力必须有势 dp f dx f dy f dz = + + ( x y z ) x f x = − y f y = − z f z = − 积分 取积分常数为零 16 f grad → = − = − i j k x y z → → → = + +