
工程流体力学 Engineering Fluld Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 流体静力学基本方程式 在重力场中,单位质量力只有重力,即: 2 1 fx=0,fv=0,f=-8 Pi 22 代入压力差公式 21 p=p(fdc+f,dy+fd正) 得:dp=-pgd→ dp dz =-P8 压强只是z的函数,水平面上各点压强相等 压强最大的变化方向在铅垂方向 z方向压强梯度为负,压强沿深度方向逐渐增大 7
Engineering Fluid Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 流体静力学基本方程式 x y z z2 z1 p1 1 p2 2 p0 o 在重力场中,单位质量力只有重力,即: f f f g x y z = = = − 0 0 , , 代入压力差公式 dp f dx f dy f dz = + + ( x y z ) dp gdz = − dp g dz 得: = − 压强只是 z 的函数,水平面上各点压强相等 压强最大的变化方向在铅垂方向 z 方向压强梯度为负,压强沿深度方向逐渐增大 17
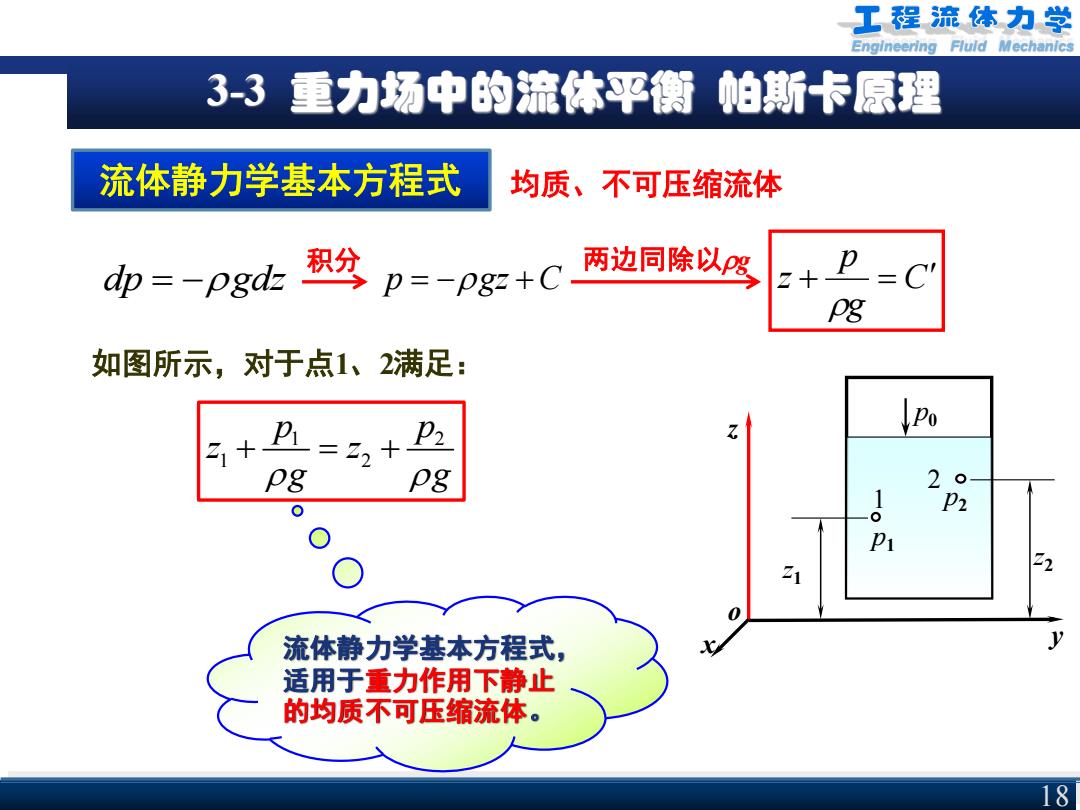
工程流体力学 Engineering Fluld Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 流体静力学基本方程式 均质、不可压缩流体 dp =-pgdz 积分 p=-pgz+C 两边同除以g Z+ pg 如图所示,对于点1、2满足: Po 21+ pg pg 2 P2 P 21 流体静力学基本方程式, 适用于重力作用下静止 的均质不可压缩流体。 18
Engineering Fluid Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 流体静力学基本方程式 x y z z2 z1 p1 1 p2 2 p0 o dp gdz = − 积分 p gz C = − + 两边同除以g 如图所示,对于点1、2满足: 1 2 1 2 p p z z g g + = + 流体静力学基本方程式, 适用于重力作用下静止 的均质不可压缩流体。 C g p z + = 18 均质、不可压缩流体
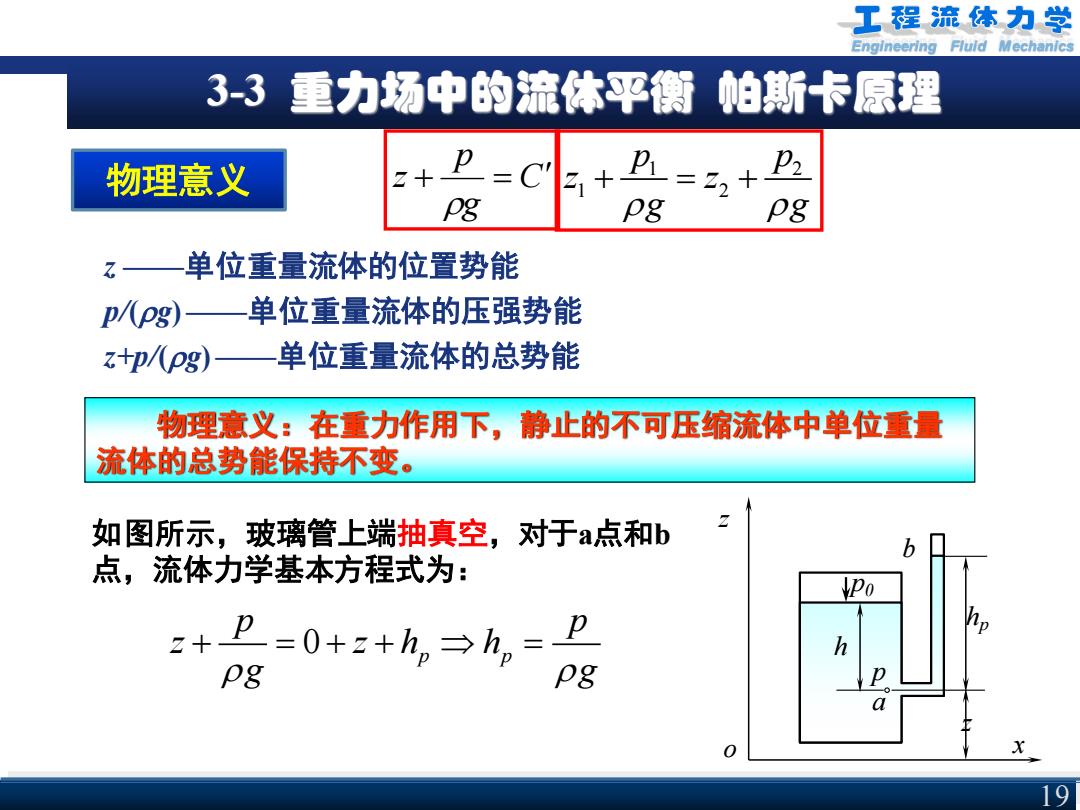
工程流体力学 Engineering Fluld Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 物理意义 =C +B=+ pg pg z—单位重量流体的位置势能 p/(pg)—单位重量流体的压强势能 z+p/(pg)—单位重量流体的总势能 物理意义:在重力作用下,静止的不可压缩流体中单位重量 流体的总势能保持不变。 如图所示,玻璃管上端抽真空,对于a点和b 点,流体力学基本方程式为: z+卫=0+z+h,→h,= pg og 0 9
Engineering Fluid Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 物理意义 C g p z + = z ——单位重量流体的位置势能 p/(g)——单位重量流体的压强势能 z+p/(g)——单位重量流体的总势能 物理意义:在重力作用下,静止的不可压缩流体中单位重量 流体的总势能保持不变。 1 2 1 2 p p z z g g + = + x z z hp a p p0 h o 如图所示,玻璃管上端抽真空,对于 b a点和b 点,流体力学基本方程式为: 0 p p p p z z h h g g + = + + = 19
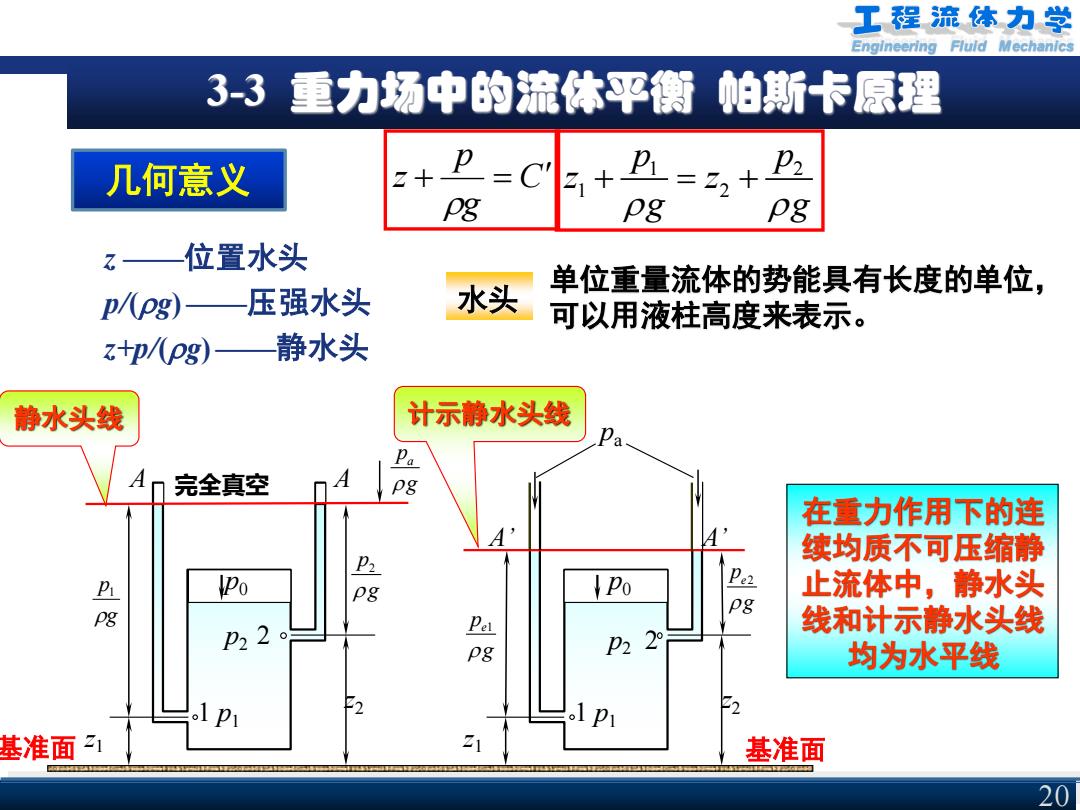
工程流体力学 Engineering Fluld Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 几何意义 z+ 31+ -=22十 pg pg pg z—位置水头 单位重量流体的势能具有长度的单位, p/(Ppg)—压强水头 水头 可以用液柱高度来表示。 z+p/(pg)—静水头 静水头线 计示静水头线 Pa 完全真空 在重力作用下的连 续均质不可压缩静 B Po Po Pe2 止流体中,静水头 pg P22 Pa 线和计示静水头线 pg P22° 均为水平线 基准面1 基准面 20
Engineering Fluid Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 几何意义 C g p z + = z ——位置水头 p/(g)——压强水头 z+p/(g)——静水头 在重力作用下的连 续均质不可压缩静 止流体中,静水头 线和计示静水头线 均为水平线 单位重量流体的势能具有长度的单位, 可以用液柱高度来表示。 水头 z1 z2 A A 1 p1 g p 1 2 p g p2 2 p0 a p g z1 z2 A’ A’ 1 p1 e1 p g e2 p g p2 2 p0 pa 完全真空 静水头线 计示静水头线 基准面 基准面 1 2 1 2 p p z z g g + = + 20

工程流体力学 Engineering Fluld Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 重力作用下静止液体内的静压力分布 对右图中淹深为h的某点a和自由液面上的 某点列静力学基本方程式 Po z+卫=(+h)+B→p5P,+pgh h 20 在重力作用下有自由表面的均质不 可压缩静止流体中的压强计算公式 静压强由两部分组成 自由表面上的压强Po,若Po发生变化,p也会变化 深度为h、密度为p的流体所产生的压强pgh 等压面(等高面):深度相同的诸点压强都相同 p=Po+pgh
Engineering Fluid Mechanics 3-3 重力场中的流体平衡 帕斯卡原理 重力作用下静止液体内的静压力分布 x y z z0 z p0 o h a 对右图中淹深为h 的某点a 和自由液面上的 某点列静力学基本方程式 ( ) g p z h g p z 0 + = + + 0 p p gh = + 在重力作用下有自由表面的均质不 可压缩静止流体中的压强计算公式 静压强由两部分组成 自由表面上的压强 p0 ,若p0发生变化,p也会变化 深度为h 、密度为 的流体所产生的压强gh 21 等压面(等高面):深度相同的诸点压强都相同 0 p p gh = +