工程流体力学 Engineering Fluld Mechanics 3-1流体静压强及其特性 流体静压强的特性 特性二 取任意微元四面体如图所示,在静止 流体中的点A取一微元四面体,与坐标轴 相重合的边长分别为、d、正,三角形 Px △BCD的面积设为S,各微小平面中心点上 8i, 的压强分别为P、P、p,单位质量力在三 个坐标轴方向上的投影分别为f、。 Py 由于流体静止,则作用在四面体上的力平衡,即: ∑Fx=0 ∑Fy=0 ∑F2=0
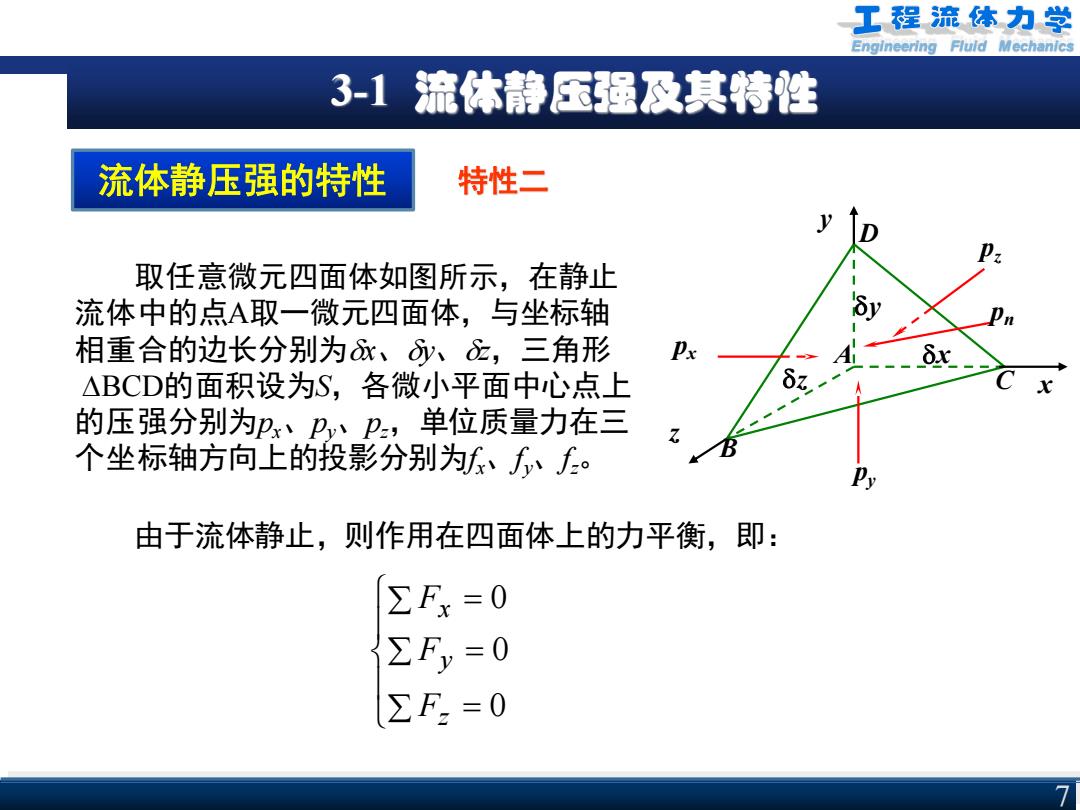
Engineering Fluid Mechanics 3-1 流体静压强及其特性 7 流体静压强的特性 x y z px pz py pn x y z A B C D 特性二 取任意微元四面体如图所示,在静止 流体中的点A取一微元四面体,与坐标轴 相重合的边长分别为x、y、z,三角形 BCD的面积设为S,各微小平面中心点上 的压强分别为px、py、pz,单位质量力在三 个坐标轴方向上的投影分别为fx、fy、f z。 由于流体静止,则作用在四面体上的力平衡,即: = = = 0 0 0 z y x F F F
工程流体力堂 Engineering Fluld Mechanics 3-1流体静压强及其特性 流体静压强的特性 特性二 @质量力 重力、惯性力 f.px5δx6y0 Px °AL--6x 6 @表面力 只有法向力 R*号0aER,×0:心Pox6xy p.3n @所受合力为零〉 流体内部无切向力,由质量力与压力平 衡可得压强大小只是作用点位置的函数 8
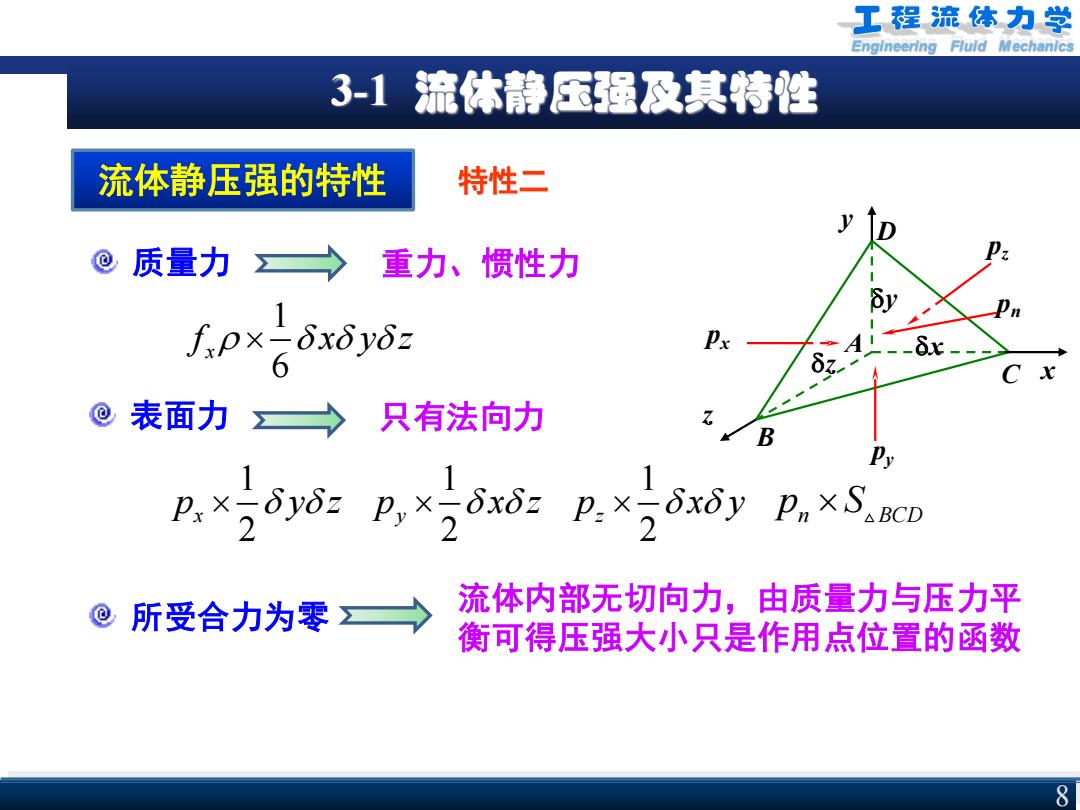
Engineering Fluid Mechanics 3-1 流体静压强及其特性 8 流体静压强的特性 特性二 x y z px pz py pn x y z A B C D 质量力 重力、惯性力 表面力 只有法向力 1 6 x f x y z 1 2 x p y z 1 2 y p x z 1 2 z p x y n BCD p S 所受合力为零 流体内部无切向力,由质量力与压力平 衡可得压强大小只是作用点位置的函数

工程流体力学 Engineering Fluld Mechanics 3-1流体静压强及其特性 流体静压强的特性 特性二 以x坐标轴方向为例,作用在四面体上的力在x方向上的平衡方程为: B.×iz+LOx16x6-p,scos(u)=0 因为:ssm,)-2定→p,+fipxòx-P.=0 略去无穷小项 Px=Pn }2=9=R 同理: Py=Pn p.=p 可见,在静止流体中任一点上任意方向的压强相等,是空间坐标 的连续函数,即: p=p(x,y,2) 9
Engineering Fluid Mechanics 3-1 流体静压强及其特性 9 流体静压强的特性 特性二 以x坐标轴方向为例,作用在四面体上的力在x方向上的平衡方程为: ( ) 1 1 cos , 0 2 6 x x n p y z f x y z p S + − = n i S ( ) yz 2 1 因为: cos n,i = 1 0 6 x x n p f p + − = x 略去无穷小项 x n p p = 同理: y n p p = z n p p = x y z n p p p p = = = 可见,在静止流体中任一点上任意方向的压强相等,是空间坐标 的连续函数,即: p = p(x, y,z)
工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 平衡微分方程式 @质量力 →fpδxdδzf=fi+fj+fk fpδxovδzfpδ.xδδz fpδxδyδz 表面力→以到→p(x±y) 泰勒级数展开 略去高阶小项 在静止流体中取一边长 △X △X 分别为、、&的微小立 p(K ,y, p(x b 方体,中心点为a(x,y,), 该点的密度为p,静压强为 y 8x 87 p(x,y,。 10
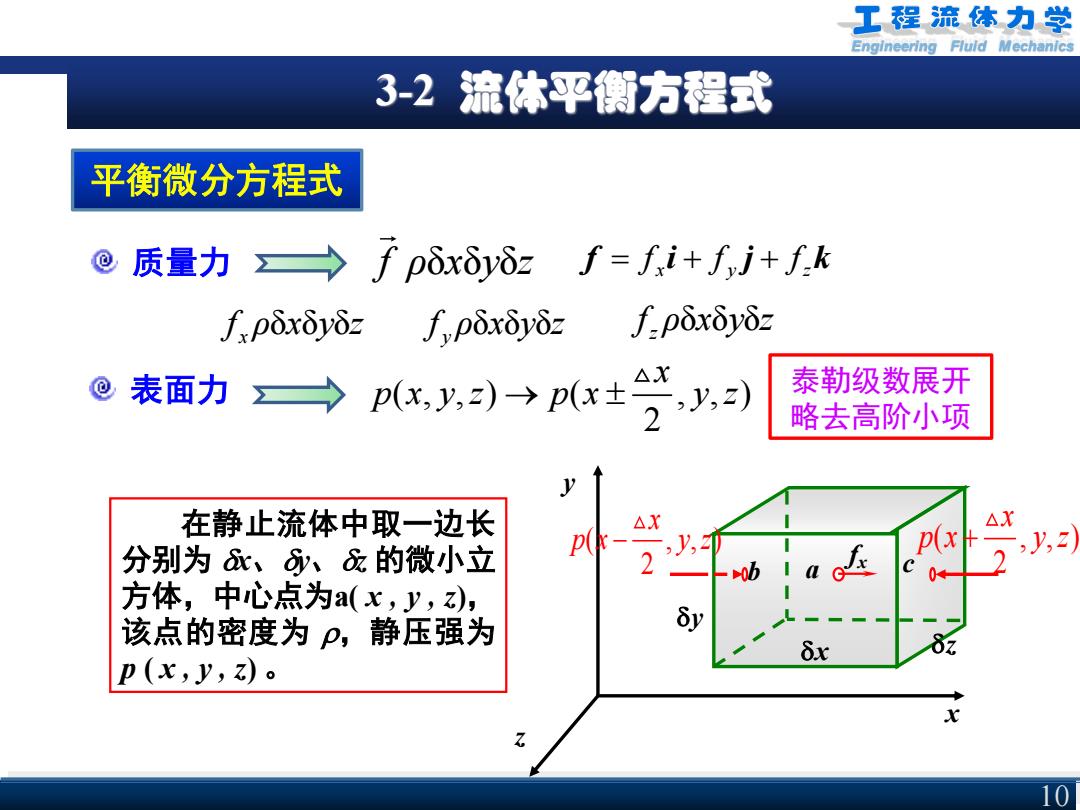
Engineering Fluid Mechanics 3-2 流体平衡方程式 10 平衡微分方程式 质量力 表面力 f ρδxyz δ δ f = f x i + f y j + f z k δ δ δ x f ρ xyz δ δ δ y f ρ xyz δ δ δ z f ρ xyz 泰勒级数展开 略去高阶小项 ( , , ) ( , , ) 2 x p x y z p x y z → 在静止流体中取一边长 分别为 x、y、z 的微小立 方体,中心点为a( x , y , z), 该点的密度为 ,静压强为 p ( x , y , z) 。 b a c x z y x y z fx ( , , ) 2 x ( , , ) p x y z + 2 x p x y z −

工程流体力学 Engineering Fluld Mechanics 3-2流体平衡方程式 平衡微分方程式 作用在立方体上的力在x方向的平衡方程为: p ]6:-e+歌5,i-nwi=0 fxpδxδyδz- 迎 δxd8z=0 op &x op 8x &x p Ox2 -0b 0x2 、 1卫=0 y 8x δz p Ox x 1 同理可得 op ≥0 pay f.- 1 ap =0 p Oz
Engineering Fluid Mechanics 3-2 流体平衡方程式 11 平衡微分方程式 作用在立方体上的力在 x 方向的平衡方程为: 0 2 2 x p x p x p y z p y z f x y z x x − − + + = b a c x z y x y z fx 2 p x p x + 2 p x p x − δ δ δ δ δ δ = 0 x y z x p f ρ x y z x - 1 0 x p f ρ x − = 同理可得 1 0 y p f y − = 1 0 z p f z − =