
由上述可见,一个随时间按正弦规律变化的电压和电 流,可以用一个称为相量的复数来表示。已知正弦电压电 流的瞬时值表达式,可以得到相应的电压电流相量。反过 来,已知电压电流相量,也能够写出正弦电压电流的瞬时 值表达式。即 (t)=Um cos(@t+yu)大o→Um=Um∠y i(t)=Imc0s(ot+y)ko→im=Im∠y
由上述可见,一个随时间按正弦规律变化的电压和电 流,可以用一个称为相量的复数来表示。已知正弦电压电 流的瞬时值表达式,可以得到相应的电压电流相量。反过 来,已知电压电流相量,也能够写出正弦电压电流的瞬时 值表达式。即 i i u u m m m m m m ( ) cos( ) ( ) cos( ) i t I t I I u t U t U U

例10-3已知正弦电流i,()=5c0s(314什60)A, 2(t)F-10sin(314t+60)A。 写出这两个正弦电流的电流相量,画出相量图,并 求出i(t)=i(t)+2()。 解:根据以下关系 i(t)=5c0s(314t+60°)A =Rel5eicei34 JA Re[iimei314 JA 得到表示正弦电流i1()=5c0s(314什60)A的相量为 i1m=5e0A=5∠60°A
例10-3 已知正弦电流i 1 (t)=5cos(314t+60)A, i 2 (t)=-10sin(314t+60)A。 写出这两个正弦电流的电流相量,画出相量图,并 求出i(t)=i 1 (t)+i 2 (t)。 Re[5e e ]A Re[ ]A ( ) 5cos(314 60 )A j314 1m j6 0 j314 1 t t I e i t t 得到表示正弦电流i 1 (t)=5cos(314t+60)A的相量为 5e A 5 60 A j60 1m I 解:根据以下关系

正弦电流与其电流相量的关系可以简单表示为 i1(C)=5c0s(314t+60)A→11m=5e160A=5∠60°A 与此相似,对于正弦电流i,()=-10sin(314t什60)A可以 得到以下结果 三角公式sinx=cos(x-90) i2(t)=-10sin(314t+60°)A =-10c0s(314t+60°-90°)A =10c0s(314t-30°+180)A→2m=10∠150°A 注意:今后在用相量法分析电路时,应该将各正弦电压 电流的瞬时表达式全部用余弦函数(正弦函数)表示
正弦电流与其电流相量的关系可以简单表示为 ( ) 5cos(314 60 )A 5e A 5 60 A j60 1 1m i t t I 10cos(314 30 180 )A 10 150 A 10cos(314 60 90 )A ( ) 10sin(314 60 )A 2m 2 t I t i t t 注意:今后在用相量法分析电路时,应该将各正弦电压 电流的瞬时表达式全部用余弦函数(正弦函数)表示。 与此相似,对于正弦电流i 2 (t)= -10sin(314t+60)A可以 得到以下结果 三角公式 sinx=cos(x-90)
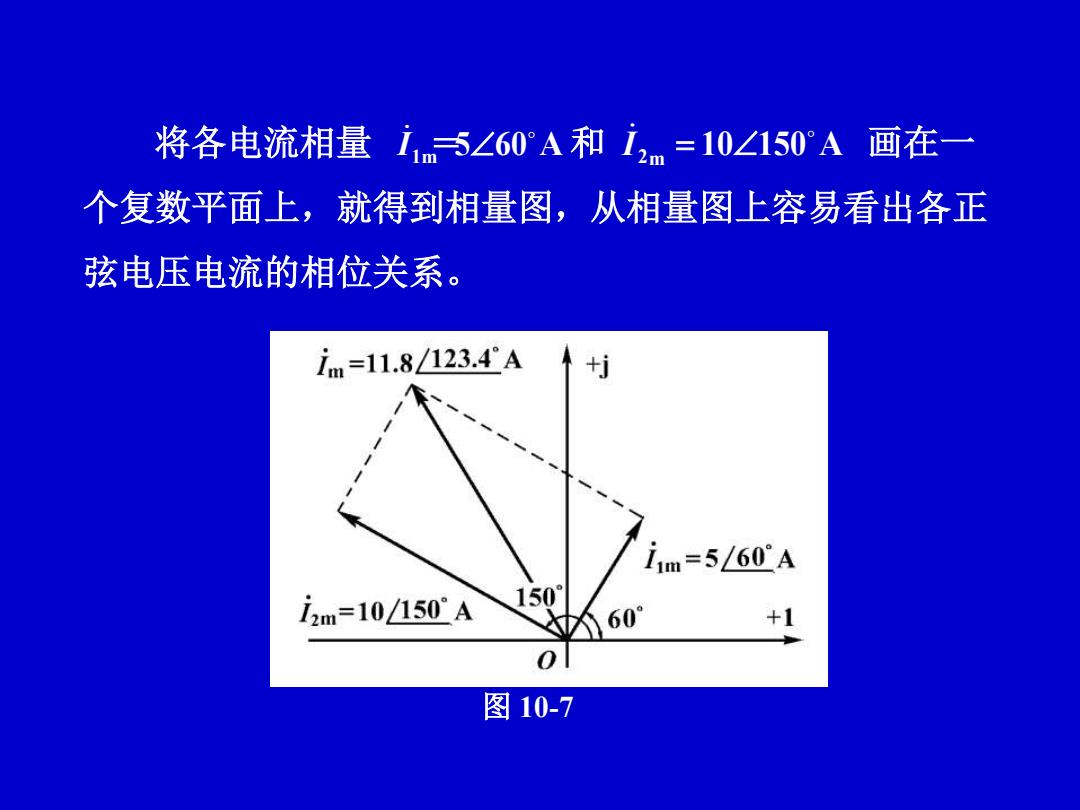
将各电流相量i1m∠60°A和i2m=10∠150°A画在一 个复数平面上,就得到相量图,从相量图上容易看出各正 弦电压电流的相位关系。 im=11.8/123.4A i1m=5/60A i2m=10/150A 150 K60 +1 0 图10-7
图 10-7 将各电流相量 和 画在一 个复数平面上,就得到相量图,从相量图上容易看出各正 弦电压电流的相位关系。 1m 5 60 A I = 2m 10 150 A I
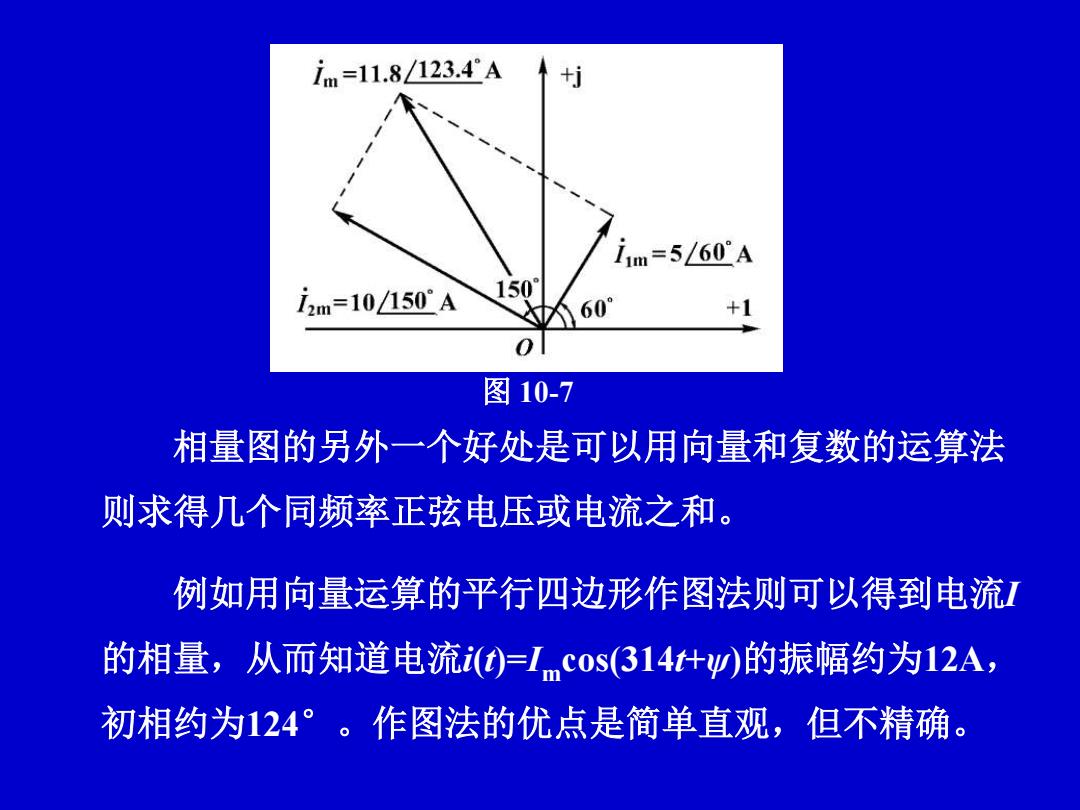
im=11.8/123.4A +j I1m=560A i2m=10/150°A 150 601 +1 0 图10-7 相量图的另外一个好处是可以用向量和复数的运算法 则求得几个同频率正弦电压或电流之和: 例如用向量运算的平行四边形作图法则可以得到电流I 的相量,从而知道电流i(t)=Icos(314+)的振幅约为12A, 初相约为124°。作图法的优点是简单直观,但不精确
相量图的另外一个好处是可以用向量和复数的运算法 则求得几个同频率正弦电压或电流之和。 例如用向量运算的平行四边形作图法则可以得到电流I 的相量,从而知道电流i(t)=Im cos(314t+ψ)的振幅约为12A, 初相约为124°。作图法的优点是简单直观,但不精确。 图 10-7