
三、正弦电压电流的相量表示 分析正弦稳态的有效方法是相量法,相量法的基础是 用一个称为相量的向量或复数来表示正弦电压和电流。假 设正弦电压为 u(t)=U cos(@t+) 利用它的振幅U和初相w来构成一个复数,复数的模 表示电压的振幅,其幅角表示电压的初相,即 Un=Ueiv=Um∠w
三、正弦电压电流的相量表示 ( ) cos( ) u t Um t 利用它的振幅Um和初相ψ来构成一个复数,复数的模 表示电压的振幅,其幅角表示电压的初相,即 m j m m U U e U 分析正弦稳态的有效方法是相量法,相量法的基础是 用一个称为相量的向量或复数来表示正弦电压和电流。假 设正弦电压为
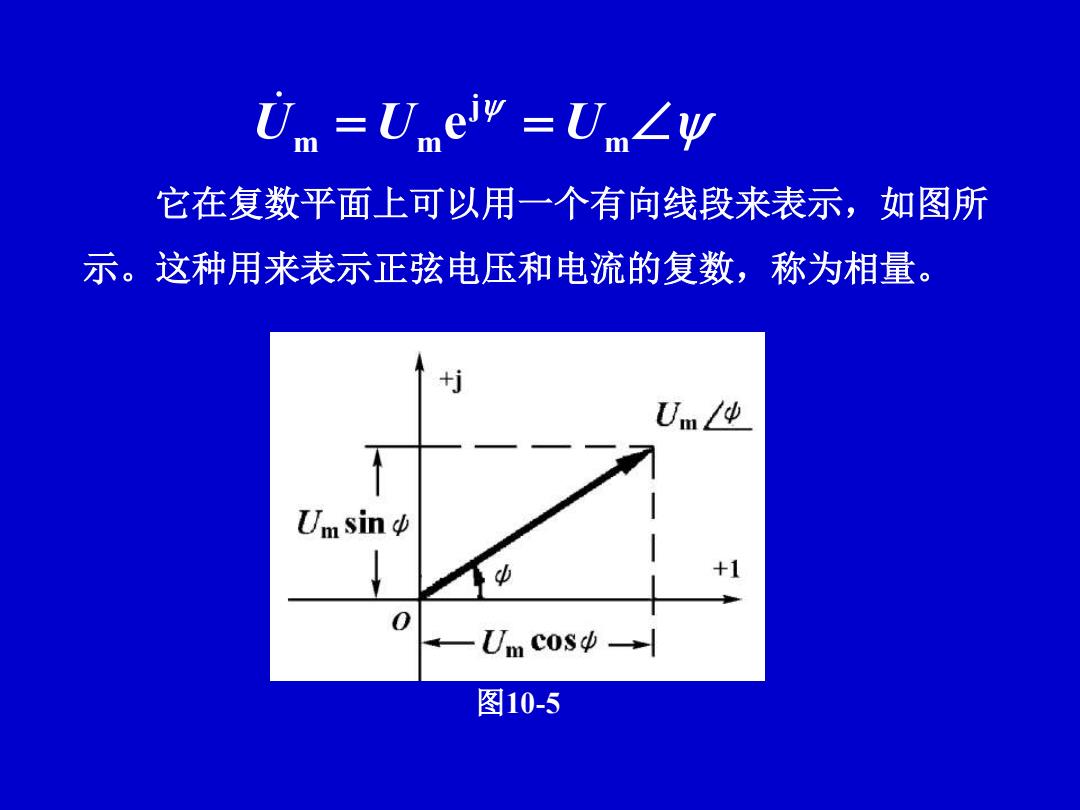
☑n=Umew=Um∠y 它在复数平面上可以用一个有向线段来表示,如图所 示。这种用来表示正弦电压和电流的复数,称为相量。 UmLo Umsin +1 Um cos→ 图10-5
它在复数平面上可以用一个有向线段来表示,如图所 示。这种用来表示正弦电压和电流的复数,称为相量。 m j m m U U e U 图10-5
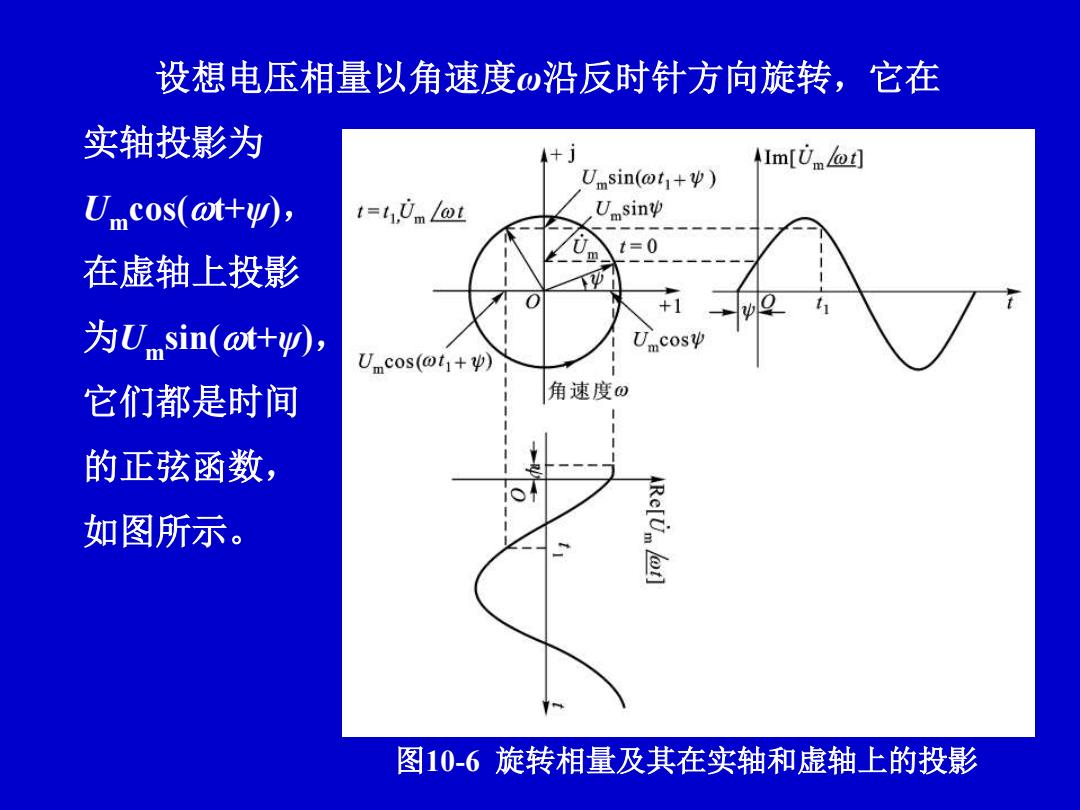
设想电压相量以角速度ω沿反时针方向旋转,它在 实轴投影为 Im[U ot] Umsin(ot1+ψ) Ucos(ot+), t=4,0m@L Umsin t=0 在虚轴上投影 为sin(ot+y, Umcos(@t+) 它们都是时间 角速度@ 的正弦函数, 如图所示。 Rc[Um ot] 图10-6旋转相量及其在实轴和虚轴上的投影
设想电压相量以角速度ω沿反时针方向旋转,它在 实轴投影为 Um cos(t+ψ), 在虚轴上投影 为Um sin(t+ψ), 它们都是时间 的正弦函数, 如图所示。 图10-6 旋转相量及其在实轴和虚轴上的投影

将电压相量 Um =Umei 与旋转因子 eia-cosattjsin@t 相乘可以得到以下数学表达式 Uei=U) =U cos(@t +)+jUm sin(@t +u
将电压相量 ψ U U j m m e 与旋转因子 e jt=cost+jsin t 相乘可以得到以下数学表达式 cos( ) j sin( ) e e m m j( ) m j t m U t ψ U t ψ U U t ψ

上式表明正弦电压与电压相量之间的关系为 ReUei]=Um cos(@t+y) Imlei]=U sin(@t+y) 由此可得 u(t)=Umc0s(ot+业) =ReUei)
上式表明正弦电压与电压相量之间的关系为 Im[ e ] sin( ) Re[ e ] cos( ) m j t m m j t m U U t ψ U U t ψ ω ω 由此可得 Re( e ) ( ) cos( ) j m m t U u t U t ψ