
线性系统的性质: ●叠加性:x(t),x2(起的输出分别为 (如输)… 入为 x(t)则输出为 y(t)+y2(t)+. ●比例特性(齐次性)如x起的输出为则叫 引起鲍输出为 。 ay(t) ●微分特性:(引起的输出为 dy(t) dt dt ○积分特性」x()鸡引起的输出为 ∫yt)d ●频率保持性:如x(t)=x财o y(t)=yoei(t+)
线性系统的性质: ●叠加性: 引起的输出分别为 如输 入为 则输出为 ●比例特性(齐次性):如 引起的输出为 ,则 引起的输出为 。 ●微分特性: 引起的输出为 ●积分特性: 引起的输出为 ●频率保持性:如 则 x t( ) ay t( ) dx t( ) dt 1 2 x t x t ( ) ( ) + + 1 2 y t y t ( ) ( ) + + 1 2 x t x t ( ), ( ) 1 2 y t y t ( ), ( ) y t( ) ax t( ) dy t( ) dt 0 ( ) t x t dt 0 ( ) t y t dt 0 0 ( ) j t x t x e = 0 0 ( ) 0 ( ) j t y t y e + =

重要猪论: 线性系统具有频率保持特性的含义是输入信号的 频率成分通过线性系统后仍保持原有的频率成分 ◆根据输入信号的频率成分确定输出信号的频率成 分,识别输出信号的真伪及噪声、干扰; ◆比较输入输出信号的频率成分,判断系统是否为 线性系统
重要结论: 线性系统具有频率保持特性的含义是输入信号的 频率成分通过线性系统后仍保持原有的频率成分。 ◆根据输入信号的频率成分确定输出信号的频率成 分,识别输出信号的真伪及噪声、干扰; ◆比较输入输出信号的频率成分,判断系统是否为 线性系统
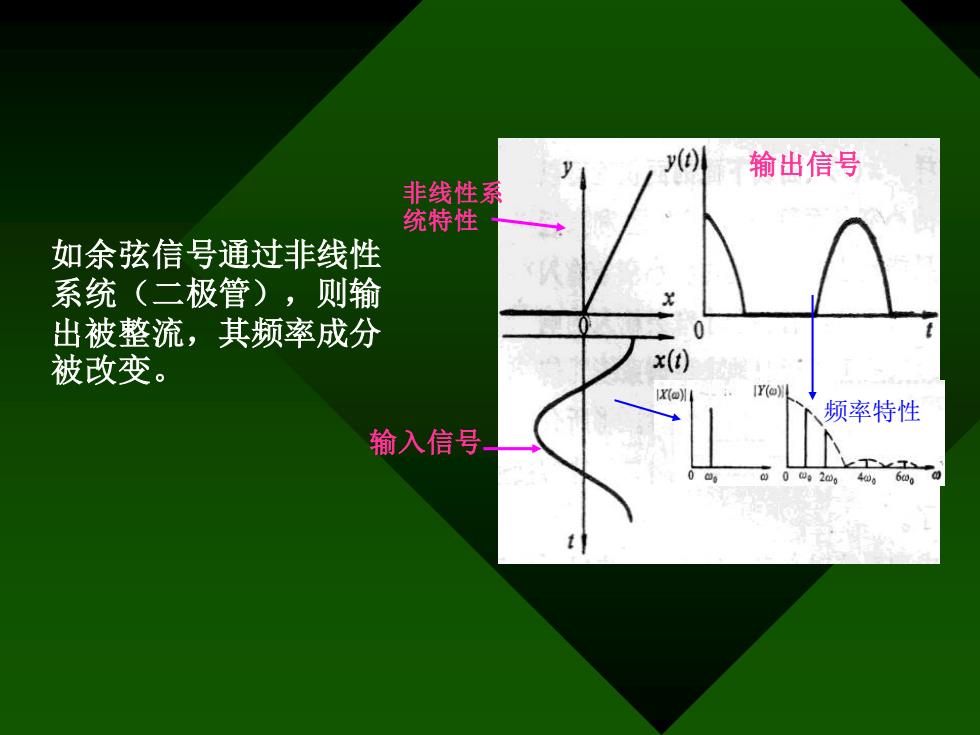
输出信号 非线性系 统特性 如余弦信号通过非线性 系统(二极管),则输 出被整流,其频率成分 被改变。 x() IX(o) Y(o 频率特性 输入信号 02064。6
如余弦信号通过非线性 系统(二极管),则输 出被整流,其频率成分 被改变。 输入信号 输出信号 非线性系 统特性 频率特性

2.2.1测试系统的广义数学模型 测试系统的数学模型是根据相应的物理定律(如牛顿定律、 能量守恒定律、基尔霍夫电路定律等)而得出的一组将输入 和输出联系起来的数学方程式。 ◇常系数线性微分方程(Genera1 Differentia1 l equation) - 线性时不变系统可用常系数线性微分方程来描述其输入x(t)和 输出y(t)之间的关系。 dy() d"-y() dy(t an d dt"- +…+a4 dt 2+ay() dx( ( m +…+b dt" dt L+bx() ·a,an-1,…,ao,bn,bmr1,…,bo是由系统本身物理参数所决 定的常数 ·系统的阶次由输出量最高微商阶次n决定
2.2.1 测试系统的广义数学模型 测试系统的数学模型是根据相应的物理定律(如牛顿定律、 能量守恒定律、基尔霍夫电路定律等)而得出的一组将输入 和输出联系起来的数学方程式。 常系数线性微分方程(General Differential equation) –线性时不变系统可用常系数线性微分方程来描述其输入x(t)和 输出y(t)之间的关系。 • an,an-1,…,a0,bm,bm-1,…,b0是由系统本身物理参数所决 定的常数 • 系统的阶次由输出量最高微商阶次n决定。 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 0 1 1 1 1 0 1 n n n n n n m m m m m m d y t d y t dy t a a a a y t dt dt dt d x t d x t dx t b b b b x t dt dt dt − − − − − − + + + + = + + + +
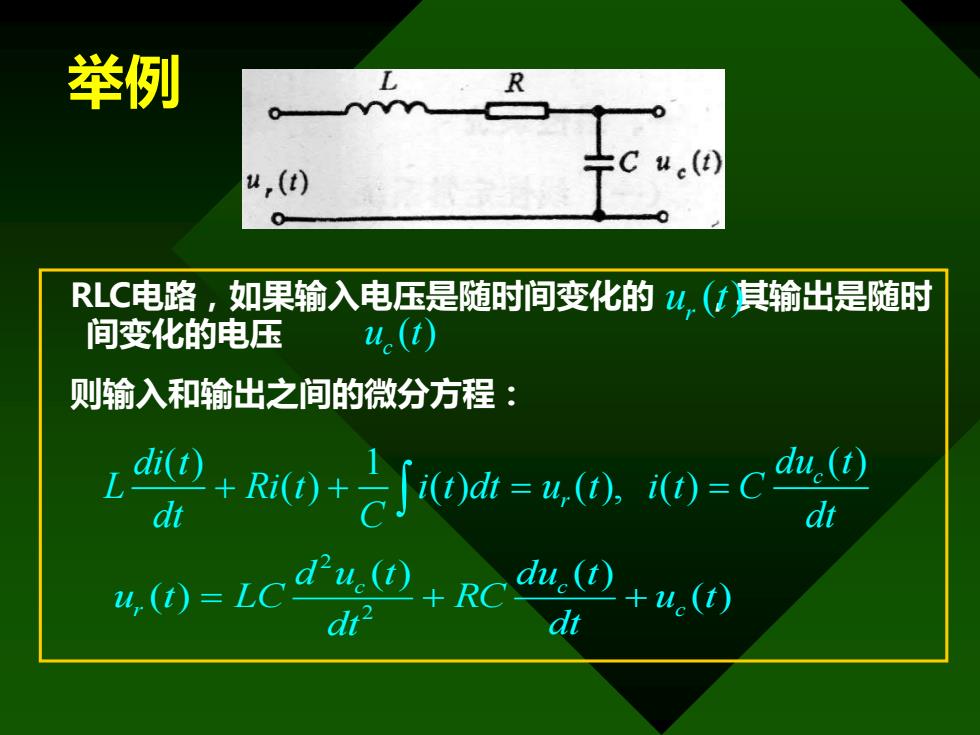
举例 u,(t) Cu() RLC电路,如果输入电压是随时间变化的4.(t其输出是随时 间变化的电压 u.(t) 则输入和输出之间的微分方程: 90+2ua=m0=c dt (=LC+RC du (t) dt2 dt +u.(
举例 RLC电路,如果输入电压是随时间变化的 ,其输出是随时 间变化的电压 则输入和输出之间的微分方程: 2 2 ( ) ( ) ( ) ( ) c c r c d u t du t u t LC RC u t dt dt = + + ( ) r u t ( ) c u t ( ) 1 ( ) ( ) ( ) ( ), ( ) c r di t du t L Ri t i t dt u t i t C dt C dt + + = =