《数学建模与数学实验》教学教学资源（PPT课件）第13讲 拟合

线性最小二乘法的求解 所以，曲线拟合的最小二乘法要解决的问题，实际上就是 求以下超定方程组的最小二乘解的问题. Ra-y (3) (x) (x) 其中R= 5(xn) 定理：当RR可逆时，超定方程组（3)存在最小二乘 解，且即为方程组 RTRa=RTy 的解：a=(RRRy

线性最小二乘法的求解 定理：当RTR可逆时，超定方程组（3）存在最小二乘 解，且即为方程组 RTRa=RTy 的解：a=(RTR) -1RTy 所以，曲线拟合的最小二乘法要解决的问题，实际上就是 求以下超定方程组的最小二乘解的问题． 1 1 1 1 1 1 ( ) ( ) , , ( ) ( ) m n m n m n r x r x a y R a y r x r x a y             = = =                   其中 Ra=y （3）

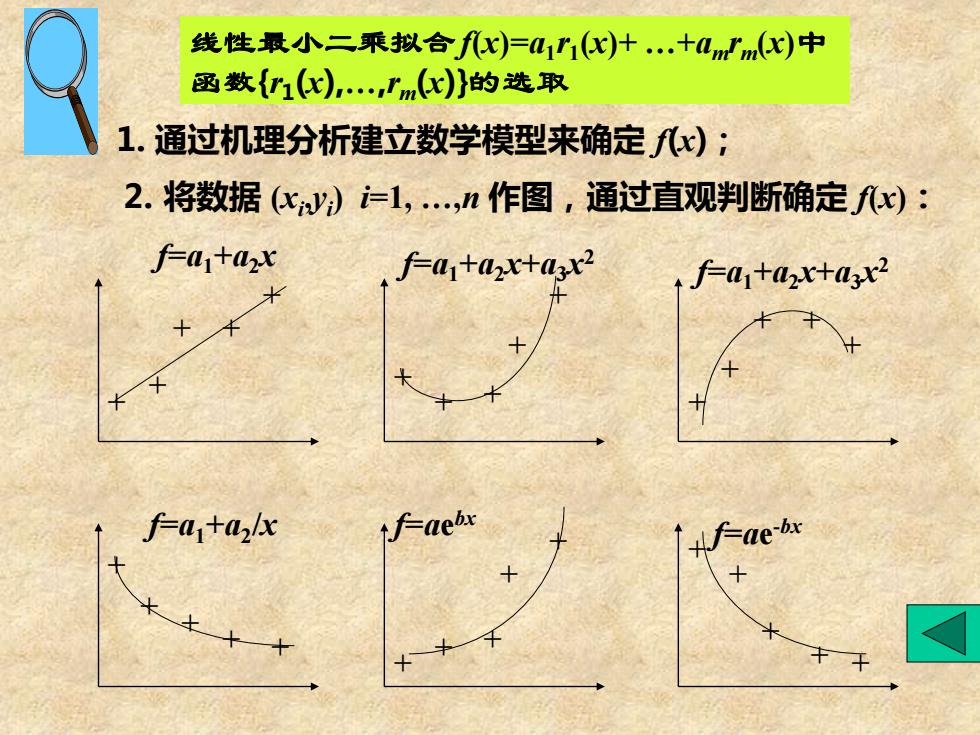
线性最小二乘拟合f八)=1（心）+.+mm)中 函数{1()Im)}的选取 1.通过机理分析建立数学模型来确定f八x): 2.将数据(c)=1,.,n作图，通过直观判断确定fx): fatax f斤a1+2x+r2 +f户a1+2x+ax2 十 f戶41+2lx -BX

线性最小二乘拟合f(x)=a1 r1 (x)+ .+amrm(x)中 函数{r1 (x),.,rm(x)}的选取 1. 通过机理分析建立数学模型来确定 f(x)； + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + f=a1+a2x f=a1+a2x+a3x 2 f=a1+a2x+a3x 2 f=a1+a2 /x f=ae bx f=ae -bx 2. 将数据 (xi ,yi ) i=1, .,n 作图，通过直观判断确定 f(x)：

用MATLAB解拟合问题 1.线性最小二乘拟合 2.非线性最小二乘拟合

用MATLAB解拟合问题 1.线性最小二乘拟合 2.非线性最小二乘拟合

用MATLAB作线性最小二乘拟合 1.作多项式fx)=axm+.+ax+m+1拟合，可利用已有程序： a=polyfit(x,y,m) 输出拟合多项式系数 输入同长度 拟合多项 a=[a1,.,am,am+1](数组)) 的数组x,y 式次数 2.对超定方程组R,man=y(m<n）,用a=R\y 可得最小二乘意义下的解. 3.多项式在x处的值y可用以下命令计算： y=polyval (a,x)

用MATLAB作线性最小二乘拟合 1. 作多项式f(x)=a1x m+ .+amx+am+1拟合,可利用已有程序: a=polyfit(x,y,m) 2. 对超定方程组 ( ) Rnm am1 = yn1 m  n 可得最小二乘意义下的解． ，用 a = R \ y 3.多项式在x处的值y可用以下命令计算： y=polyval（a，x） 输出拟合多项式系数 a=[a1, .,am , am+1] (数组)） 输入同长度 的数组x，y 拟合多项 式次数

例对下面一组数据作二次多项式拟合 0.1 0.2 0.3 04 0.5 0.6 0.7 0.8 0.9 1.0 1.1 -0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2 即要求出二次多项式： f(x)=ax2 +ax+as 中的A=(a1,a2,a4)使得： x)-y最小 i-1

即要求 出二次多项式: 2 3 2 1 f (x) = a x + a x + a 中 的 ( , , ) A = a1 a2 a3 使得: [ ( ) ] 最小 1 1 1 2 = − i i i f x y 例 对下面一组数据作二次多项式拟合 xi 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 yi -0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2