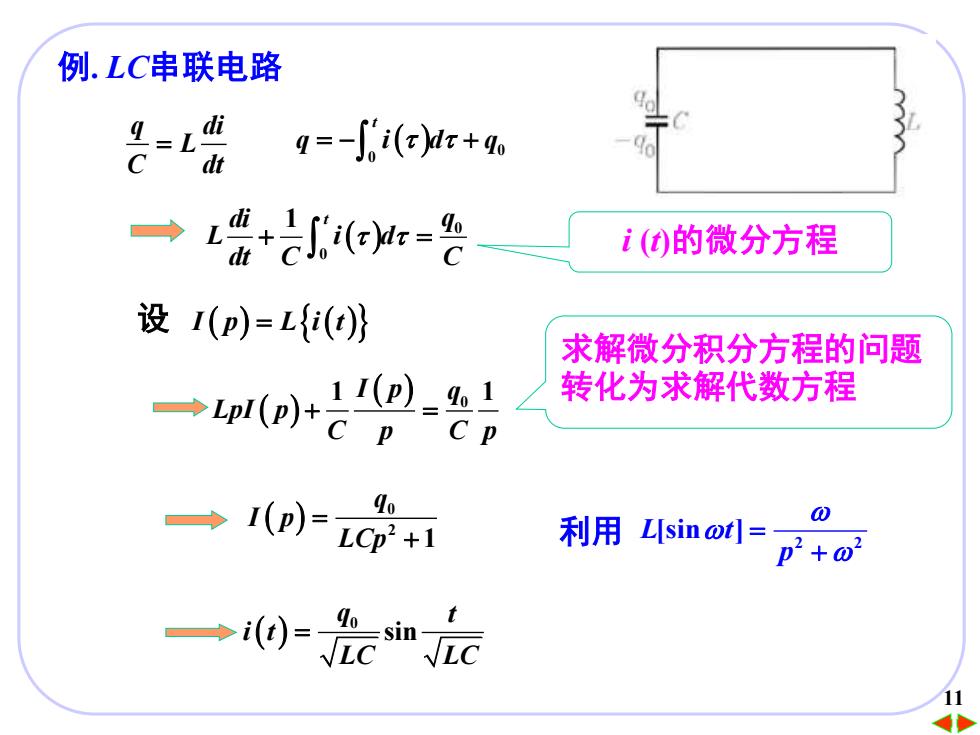
例.LC串联电路 q=-Si(=)lr+qo +a(=名 i()的微分方程 设(p)=L(t)》 求解微分积分方程的问题 ,1(p-1 →pl(p)+cp 转化为求解代数方程 C卫 一(p)=d o 利用[sin @t]= ⊙ +02
1111 例. LC串联电路 q di L C dt = ( ) 0 0 t q i d q = − + ( ) 0 0 di 1 t q L i d dt C C + = i (t)的微分方程 设 I p L i t ( ) = ( ) ( ) ( ) 1 1 0 I p q LpI p C p C p + = 求解微分积分方程的问题 转化为求解代数方程 ( ) 0 2 1 q I p LCp = + ( ) 0 sin q t i t LC LC = 2 2 L t [sin ] p = + 利用

质4若I=FD,则4r·f④1=(场 【证明】F(p)=∫fed 像微分性质 F-广-es=-okra →4r-fo=-aFp) $r=rea=irea dp 心I-多om 多rp=厂-rfoa=-wfrsok*h 4f1=(-1 F(p) dp" 12
1212 L f t F p [ ( )] ( ) = [ ( )] ( 1) ( ) n n n n d L t f t F p dp 性质4:若 ,则 = − 【证明 】 0 ( ) ( ) pt F p f t e dt − = 0 0 ( ) ( ) [ ( )] d pt pt F p t f t e dt t f t e dt dp − − = − = − 2 2 2 2 2 0 0 ( ) ( ) ( ) ( 1) [ ( )] d pt pt F p t f t e dt t f t e dt dp − − = − = − . 0 0 ( ) ( ) ( ) ( 1) [ ( )] n n pt n n pt n d F p t f t e dt t f t e dt dp − − = − = − [ ( )] ( ) d L t f t F p dp = − [ ( )] ( 1) ( ) n n n n d L t f t F p dp = − 2 2 2 2 [ ( )] ( 1) ( ) d L t f t F p dp = − 像微分性质

例: 4六 ]= D47 性质5:(延迟定理)若LLf(t)川=F(p),L[f(t-川=e"F(p) 【证明】e-训=ft-red"e-rd =∫,fu'et'+小fee+edi -0+emf(t')e Mdt'=e-"F(p) ∫fter*dt'=0,当'<0时,f)≡0. 约定 例川coswt]= p2+o2 则4cos(ot-p训=4csat-21=e p2+o2
1313 2 1 1 [ ] , d L t dp p p = − = 2 2 2 2 3 1 2! [ ] ( 1) ( ) , d L t dp p p = − = 1 L[1] , p 例 : = ., 1 ! [ ] n n n L t p + = L f t F p [ ( )] ( ), = [ ( )] ( ) p L f t e F p − 性质5:(延迟定理)若 − = 【证明 】 ' ( ' ) ' 0 [ ( )] ( ) ( ') t t pt p t L f t f t e dt f t e dt = − − − + − − = − = 令 0 ( ' ) ( ' ) 0 ( ') ' ( ') ' p t p t f t e dt f t e dt − + − + − = + ' 0 0 ( ') ' ( ) p pt p e f t e dt e F p − − − = + = 当 时, 0 ( ' ) ( ') ' 0, p t f t e dt − + − = t ' 0 f t( ') 0. 2 2 [cos ] p L t p = + 2 2 [cos( )] [cos ( )] p p L t L t e p − − = − = + 例 则 约定