
矢量分析导论 矢性函数的表示: ·矢量分解与组合满足三角法则或者平行四边形法则 ·利用正交直角坐标系把矢量分解为三个坐标方向的矢量: 。 矢性函数同样可以通过三个坐标轴上的投影分量来表示, 且其分量仍为的函数: A()=A(0x+A,()护+A()8 ·其中,x,八,2分别为x,y,轴正向的单位矢量 2018/3/6 lexu@mail.xidian.edu.cn
矢量分析导论 2018/3/6 lexu@mail.xidian.edu.cn 11 • 矢性函数的表示: • 矢量分解与组合满足三角法则或者平行四边形法则 • 利用正交直角坐标系把矢量分解为三个坐标方向的矢量; • 矢性函数同样可以通过三个坐标轴上的投影分量来表示, 且其分量仍为t的函数: • 其中, 分别为x,y,z轴正向的单位矢量
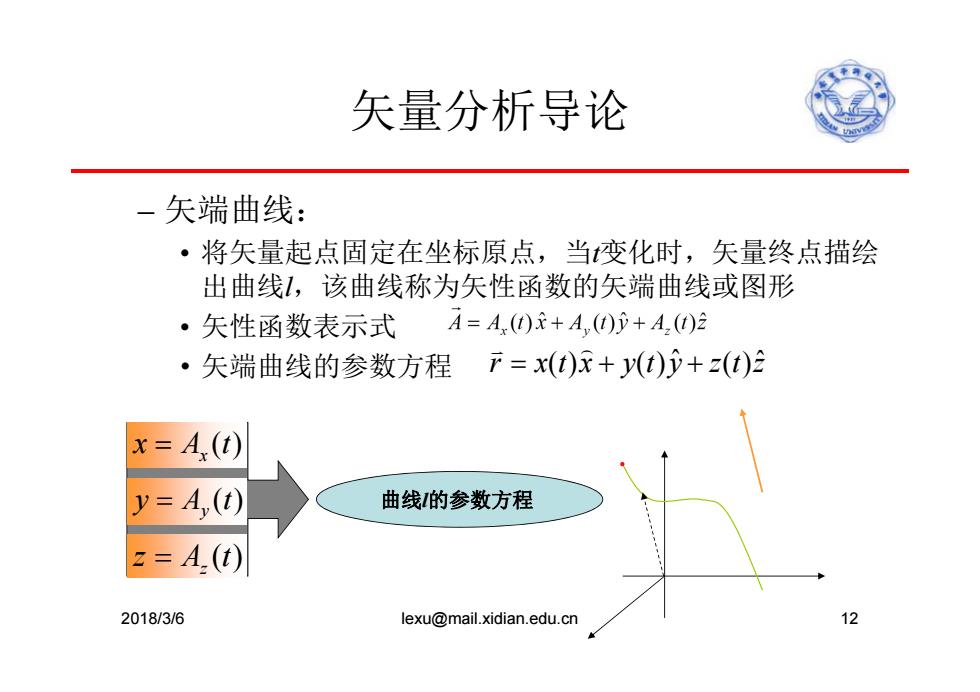
矢量分析导论 -矢端曲线: ·将矢量起点固定在坐标原点,当变化时,矢量终点描绘 出曲线1,该曲线称为矢性函数的矢端曲线或图形 ·矢性函数表示式 A=A()R+A())+A,(t)2 ·矢端曲线的参数方程 下=x(t)x+y(t)少+z(t)2 x=A(t) y=A,(t) 曲线的参数方程 z=A.(t) 2018/3/6 lexu@mail.xidian.edu.cn 12
矢量分析导论 – 矢端曲线: • 将矢量起点固定在坐标原点,当t变化时,矢量终点描绘 出曲线l,该曲线称为矢性函数的矢端曲线或图形 • 矢性函数表示式 • 矢端曲线的参数方程 2018/3/6 lexu@mail.xidian.edu.cn 12 r xtx yt y ztz () () () ˆ ˆ x A (t) x y A (t) y z A (t) z 曲线l的参数方程

矢量分析导论 矢性函数的导数与微分 dA △d -导数 d N-0△t -设是的矢性函数,当数性变量t在 dAy + 其定义域内从t变到t+△t(△t≠0)时, dt dt dt 对应的矢量从4)变化到A(t+△t),则 称△A=At+△)-A(t)为A(t)对应于△t的 增量。 △A -令:lim lim At+△)-A(t) 4(D) △A A1-→0△t △1→0 △t A(t+△t) 若极限存在,则称矢性函数在处可导,° 且为矢性函数在t处的导数。 2018/3/6 lexu@mail.xidian.edu.cn 13
矢量分析导论 • 矢性函数的导数与微分 – 导数 – 设 是t的矢性函数,当数性变量t在 其定义域内从t变到 时, 对应的矢量从 变化到 ,则 称 为 对应于 的 增量。 – 令: 若极限存在,则称矢性函数在t处可导, 且为矢性函数在t处的导数。 2018/3/6 lexu@mail.xidian.edu.cn 13 O 0 lim t dA A dt t z dt dA y dt dA x dt dAx y z ˆ ˆ ˆ
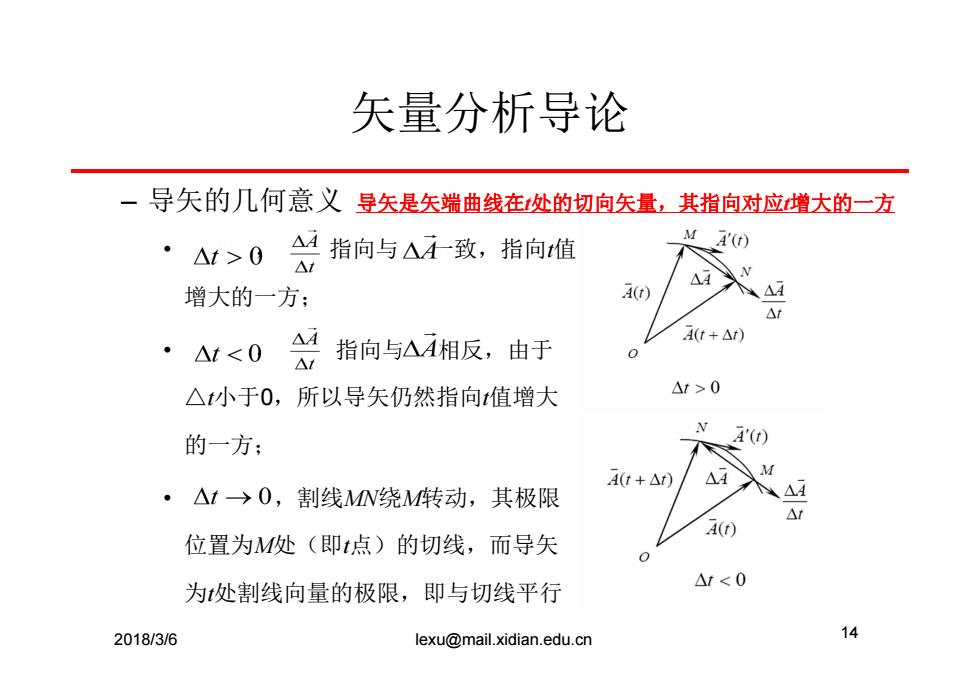
矢量分析导论 一导矢的几何意义导矢是矢端曲线在处的切向矢量,其指向对应增大的一方 M ·△t>0 会指向与△致,指向值 4() △A 增大的一方: A() △4 △f ·△1<0指向与△A相反,由于 A(t+△r) △小于0,所以导矢仍然指向值增大 △t>0 N 的一方; A'(t) At+△r) M ·△t→O,割线MN绕M转动,其极限 △d A(t) 位置为M处(即t点)的切线,而导矢 为处割线向量的极限,即与切线平行 △r<0 2018/3/6 lexu@mail.xidian.edu.cn 14
矢量分析导论 – 导矢的几何意义 • , 指向与 一致,指向t值 增大的一方; • , 指向与 相反,由于 △t小于0,所以导矢仍然指向t值增大 的一方; • ,割线MN绕M转动,其极限 位置为M处(即t点)的切线,而导矢 为t处割线向量的极限,即与切线平行 2018/3/6 lexu@mail.xidian.edu.cn 14 导矢是矢端曲线在t处的切向矢量,其指向对应t增大的一方

矢量分析导论 设A=A0,B=()和1=u)可导,则有: 1°dc=0 (—常矢量) 4° (uA)= dA d d dt dt 2da±月= dB 5° dt dt d(.B= 疗+月B dA d dt dt 3”团0=k4 (k—常数) 6 A dB d (axB)= xB+A× dt dt 7°复合函数的导数 设A=A(),u=u(),则: dAdA du dt du di 2018/3/6 lexu@mail.xidian.edu.cn 15
矢量分析导论 2018/3/6 lexu@mail.xidian.edu.cn 15