
6 功率信号和能量信号 连续时间信号的 信号的能量: 在整个时间轴上,E=fuah 信号的功率: 在整个时间轴上, mn 离散时间信号 能量E=8xn 功率P=lim 1立xnl N→o2N+1n=- UX
X 第 16 6. 功率信号和能量信号 页 连续时间信号的 信号的能量: 在整个时间轴上, 信号的功率: 在整个时间轴上, ∫∞−∞ E = f t dt 2 ( ) ( ) ] 1 lim[ 2 2 2 ∫ →∞ − = T T T f t dt T P 2 E x[n ] n ∞ = −∞ = Σ 2 [ ] 2 1 1 lim x n N P N N → ∞ n = − N Σ + = 离散时间信号 能量 功率

·例x(t)=Ac0s(wt+O) 功率型信号,功率为A22 .例0- e", t20 else ● 能量为1/2a 0-女a8 else ·非功非能信号 UX
X 第 17 页 • 例 • 功率型信号,功率为A2/2 • 例 • 能量为1/2a • 非功非能信号 ( ) cos( ) x t = A w0t +θ ⎩⎨⎧ ≥ = −0 , else , 0 ( ) e t x t at ⎩⎨⎧ ≥ = 0, else , 0 ( ) t t x t

>功率信号: 平均功率为有限值而信号总能量为无限大。 (0<P<∞,E+∞) >能量信号: 能量为有限值而平均功率为零。 (0<E<∞,P=0) 非功非能信号: (E→∞,P+∞) UX
X 第 18 页 ¾功率信号: 平均功率为有限值而信号总能量为无限大。 (0<P<∞,E→∞) ¾能量信号: 能量为有限值而平均功率为零。 ( 0<E<∞,P=0) 非功非能信号: (E→∞,P→∞)

二.几种典型确定性信号 1.指数信号 信号的表示 2.正弦信号 ·函数表达式ft) ●波形 3.复指数信号(表达具有普遍意义) 3.抽样信号(Sampling Signal) 5.钟形脉冲函数(高斯函数) UX
X 第 19 二.几种典型确定性信号 页 5.钟形脉冲函数(高斯函数) 1.指数信号 2.正弦信号 3.复指数信号(表达具有普遍意义) 3. 抽样信号(Sampling Signal) 信号的表示 函数表达式 f ( t ) 波形
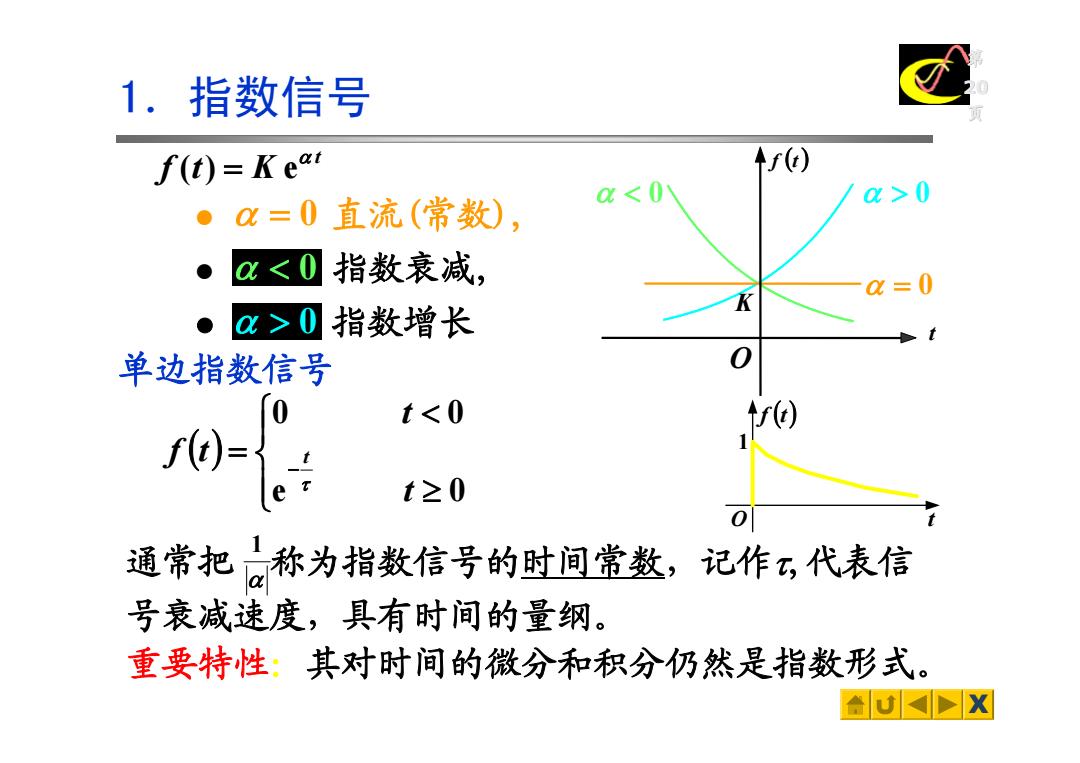
1.指数信号 f(t)=Kear ↑f) a<0 a>0 ●0=0 直流(常数), a<0 指数衰减, a=0 ●a>0指数增长 单边指数信号 0 t<0 ) f)= t≥0 0 通常把称为指数信号的时间常数,记作?,代表信 号衰减速度,具有时间的量纲。 重要特性:其对时间的微分和积分仍然是指数形式。 UX
X 第 20页 重要特性:其对时间的微分和积分仍然是指数形式。 1.指数信号 t f t K α ( ) = e 单边指数信号 通常把 称为指数信号的时间常数,记作 τ,代表信 号衰减速度,具有时间的量纲。 α 1 z α < 0 指数衰减, α < 0 z α > 0 指数增长 α > 0 z α = 0 直流(常数), K α = 0 O f ( t ) t ( ) ⎪⎩ ⎪ ⎨ ⎧ ≥ < = − e 0 0 0 t t f t t τ O t 1 f ( t )