
导期 3.填空:平面与平面平行的性质定理 ()文字语言:如果两个平行平面同时与第三个平面相交,那么 它们的交线 (2)符号语言:如果aB,a∩y=l,Bmy=m,那么lIlm (3)图形表示:如图所示
导航 3.填空:平面与平面平行的性质定理 (1)文字语言:如果两个平行平面同时与第三个平面相交,那么 它们的交线平行. (2)符号语言:如果α∥β,α∩γ=l,β∩γ=m,那么l∥m. (3)图形表示:如图所示
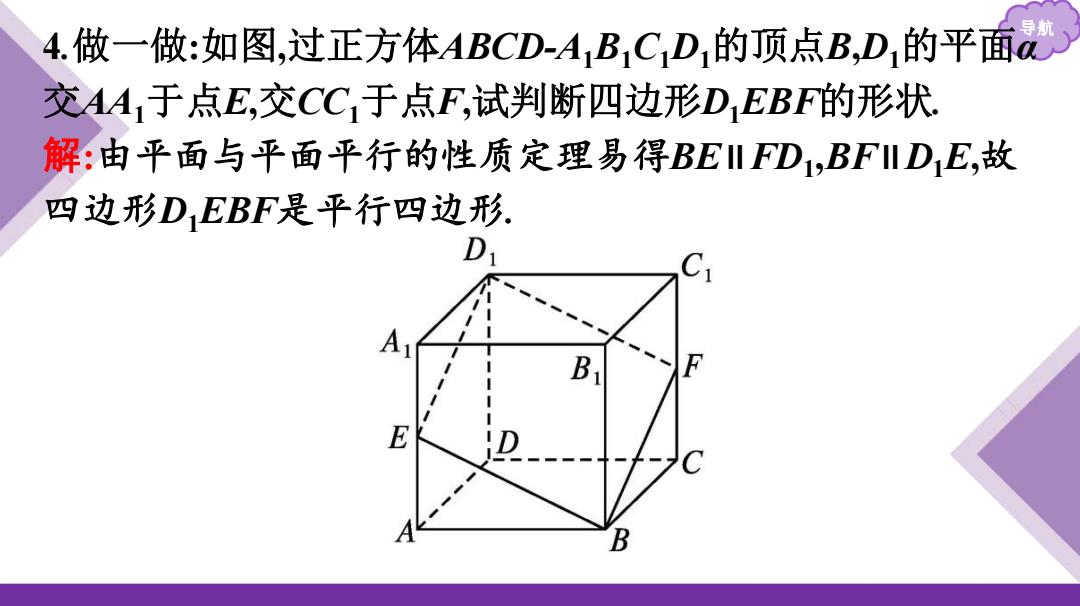
导航 4.做一做:如图,过正方体ABCD-AB1CD1的顶点B,D1的平面 交AA1于点E,交CC1于点F,试判断四边形D,EBF的形状 解:由平面与平面平行的性质定理易得BEI FD1,BFID1E,故 四边形DEBF是平行四边形 D A D E
导航 4.做一做:如图,过正方体ABCD-A1B1C1D1的顶点B,D1的平面α 交AA1于点E,交CC1于点F,试判断四边形D1EBF的形状. 解:由平面与平面平行的性质定理易得BE∥FD1 ,BF∥D1E,故 四边形D1EBF是平行四边形

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√,错误 的画“X” (1)若af,BI%则al( (2)若a内有两条直线与平面平行,则αI.(×) (3)若aI,则a内不存在与B不平行的直线.(√) (4)若平面a与无交点,则aR.(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“×” . (1)若α∥β,β∥γ,则α∥γ.( ) (2)若α内有两条直线与平面β平行,则α∥β.( ) (3)若α∥β,则α内不存在与β不平行的直线.( ) (4)若平面α与β无交点,则α∥β.( ) √ × √ √

导航 课堂·重难突破 探究一平面与平面平行的判定 【例1】已知在正方体ABCD-A1BC1D,中,E,F分别是 CC1,AA1的中点,求证:平面BDEI平面B1D1F 分析:要证两平面平行,只需在一个平面内找两条相交直线分 别平行于另一个平面即可(在平面BD1F中,两条相交直线 B1D1与B1F)
导航 课堂·重难突破 探究一 平面与平面平行的判定 【例1】已知在正方体ABCD-A1B1C1D1中,E,F分别是 CC1 ,AA1的中点,求证:平面BDE∥平面B1D1F. 分析:要证两平面平行,只需在一个平面内找两条相交直线分 别平行于另一个平面即可(在平面B1D1F中,两条相交直线 B1D1与B1F)

证明:设G是BB的中点, 连接FG,CG,DF,BE. FG⊥AB,AB⊥DC,.FG⊥DC ∴.四边形FGCD是平行四边形,则DF LCG. 由题设可得EBLCG,则D型EB· .四边形DFBE是平行四边形..B1 FIED .B1F4平面BDE,EDC平面BDE, B1FI平面BDE.又BD1IIBD, B1Dd平面BDE,BDC平面BDE,∴.BD1I平面BDE. ·B1D1∩B1F=B1,.平面BDEI平面B1D1F
导航 证明:设G是BB1的中点, 连接FG,CG,DF,B1E. ∵FG AB,AB DC,∴FG DC. ∴四边形FGCD是平行四边形,则DF CG. 由题设可得EB1 CG,则DF EB1 . ∴四边形DFB1E是平行四边形.∴B1F∥ED. ∵B1F⊄平面BDE,ED⊂平面BDE, ∴B1F∥平面BDE.又B1D1∥BD, B1D1⊄平面BDE,BD⊂平面BDE,∴B1D1∥平面BDE. ∵B1D1∩B1F=B1 ,∴平面BDE∥平面B1D1F