第四节液体的相对平衡 工程中除了重力场中的流体平衡问题以外,还有一种在工程上常见的所谓液体的相对平 衡问题,即液体质点彼此之间没有相对运动,但盛流体的容器却相对地面上的固定坐标系有 相对运动。此类问题如果我们把运动坐标系取在容器上,则对于此坐标系,液体即成为相对 平衡问题。 如果容器只有匀速直线运动,则流体质点的质量力仍与重力场中的情况完全一样,完全 可以采用不可压缩流体的静压强公式(2-28)。因此这里不必论述。工程中常见的相对平衡问 题有下面两种。 一、容器做匀加速直线运动 77777777777777777778%77 图2-10匀加速直线运动
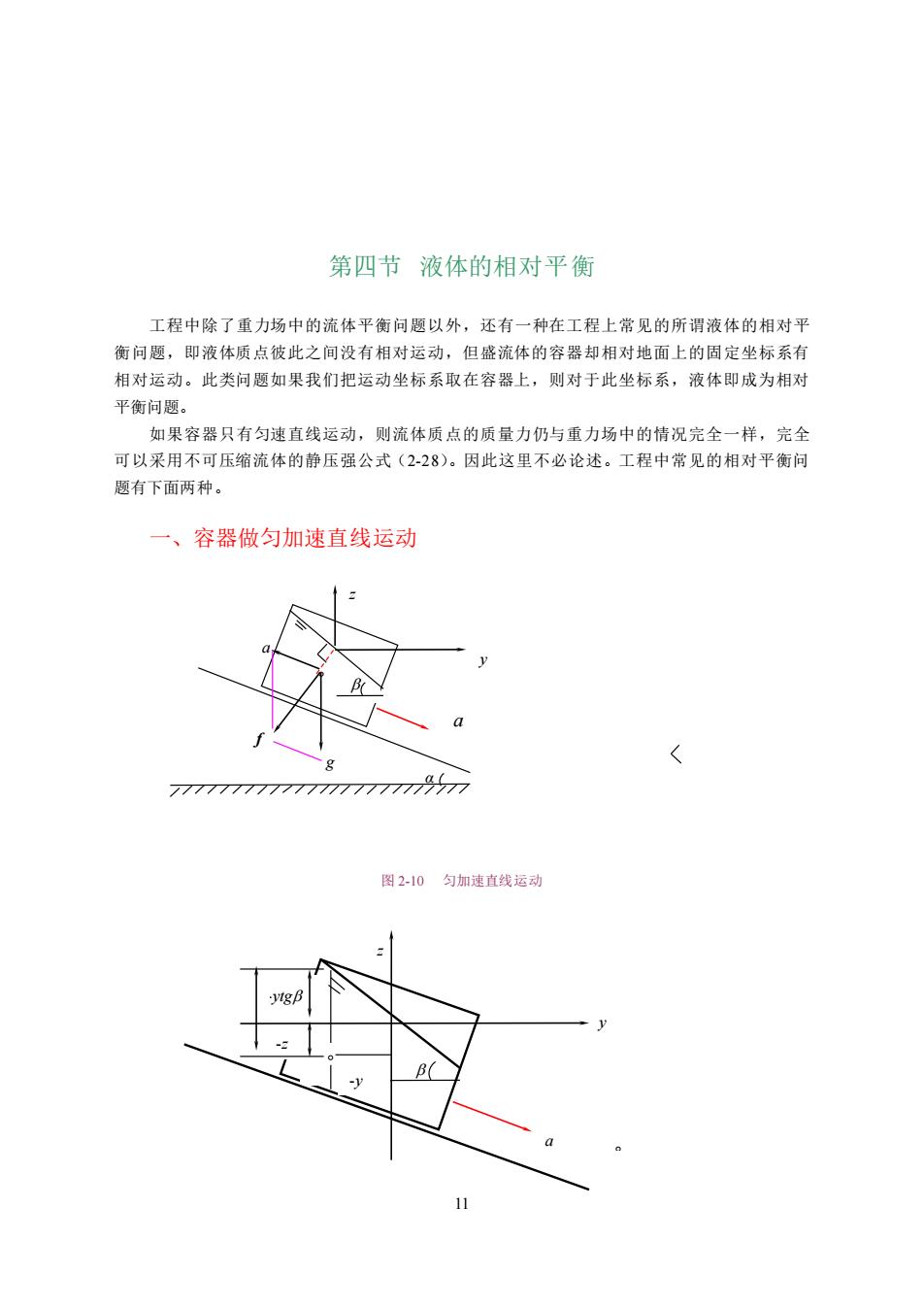
11 第四节 液体的相对平衡 工程中除了重力场中的流体平衡问题以外,还有一种在工程上常见的所谓液体的相对平 衡问题,即液体质点彼此之间没有相对运动,但盛流体的容器却相对地面上的固定坐标系有 相对运动。此类问题如果我们把运动坐标系取在容器上,则对于此坐标系,液体即成为相对 平衡问题。 如果容器只有匀速直线运动,则流体质点的质量力仍与重力场中的情况完全一样,完全 可以采用不可压缩流体的静压强公式(2-28)。因此这里不必论述。工程中常见的相对平衡问 题有下面两种。 一、容器做匀加速直线运动 a 图 2-10 匀加速直线运动 a g f α A -ytg H -z z y a -y z y

77777777777777777777777 图2-11 不失一般性,如图2-10所示,盛有液体的容器沿与水平面成α角的斜面向下以匀加速a 作直线运动,将运动坐标系取在容器上,并使坐标原点在自由液面上,x轴垂直纸面。据达 朗贝尔原理,作用在液体上的力有重力、与运动加速度方向相反的虚构惯性力△=△m,因 此单位质量力为 f=fi+fj+fk (2-30) =-acosaj+(asin a-g)k 因此等压面方程为 d acosa asna-g-g231 所以 IgB=-acosa (2-31) asna-g 因为4,名,α均为常数,因此为常数,即等压面为与水平面成B角的一组平行平面。此 等压面与单位质量力∫的方向相垂直,这进一步验证了等压面的第二个特性 将(2-30)式代入压强微分公式(2-21),并取边界条件为 y-0,-0时p-pm 得压强分布公式为 p=po+pl-aycosa+=(asin a-g)] (2-32) 此式即为流体静压强在不同点(y,:)上的分布规律。但我们关心的是压强沿水深H的 变化,因此可将上式进行换算。 如图(21)所示,当点A位于:轴的左边,即>0时,由图中几何关系可知 H=-=-ytgB (2-33) 同样,当点A位于:轴的右边,即y<0时有 H=-=-ytgB (2-33') 所以有 :=-gB-H (2-34 将(2-34)代入(2-32)可得 p=po+pl-aycosa+(-ytgB-HXasin a-g) =Po+pl(asin a-gX-H)-aycosa-ytgB(asin a-g)] (2-35) 将(2-31)代入(2-35)得
12 图 2-11 不失一般性,如图 2-10 所示,盛有液体的容器沿与水平面成 α 角的斜面向下以匀加速 a 作直线运动,将运动坐标系取在容器上,并使坐标原点在自由液面上,x 轴垂直纸面。据达 朗贝尔原理,作用在液体上的力有重力、与运动加速度方向相反的虚构惯性力 ΔI=Δma,因 此单位质量力为 j k f i j k acos (asin g) f f f x y z = − + − = + + (2-30) 因此等压面方程为 tg a g a y z = − − = sin cos d d (2-31’) 所以 a g a tg − − = sin cos (2-31) 因为 a,g,均为常数,因此为常数,即等压面为与水平面成角的一组平行平面。此 等压面与单位质量力 f 的方向相垂直,这进一步验证了等压面的第二个特性。 将(2-30)式代入压强微分公式(2-21),并取边界条件为 y=0,z=0 时 p=p0 得压强分布公式为 [ cos ( sin )] p = p0 + −ay + z a − g (2-32) 此式即为流体静压强在不同点(y,z)上的分布规律。但我们关心的是压强沿水深 H 的 变化,因此可将上式进行换算。 如图(2-11 )所示,当点 A 位于 z 轴的左边,即 y>0 时,由图中几何关系可知 H = −z − ytg (2-33) 同样,当点 A 位于 z 轴的右边,即 y<0 时有 H = −z − ytg (2-33’) 所以有 z = −ytg − H (2-34) 将(2-34)代入(2-32)可得 [( sin )( ) cos ( sin )] [ cos ( )( sin )] 0 0 p a g H ay ytg a g p p ay ytg H a g = + − − − − − = + − + − − − (2-35) 将(2-31)代入(2-35)得: α

-acosa pp.+pl(-asn a)+p-aycosa-s(asin a-g =Po+p(g-asin a)H (2-36) Po+pH(1-asin a g 由此可知,当a,p为常数时,液体下面的点的静压强的大小只与液深H有关,当斜 面角度变为0或π/2时,即可得容器水平或铅直匀加速直线运动的两种特例。 图2-12沿水平基面作匀加速直线运动 图2-13沿垂直方向作匀加速直线运动 1.Q-0时,即容器沿水平基面匀加速运动时,如图2-12所示,由(2-31)可得等压面 方程为 =0=-g2-37) dy g 由(2-36)可得压强分布公式为 P=Po+pgH (2-38)】 此式表明,容器沿水平基面作匀加速运动时的表压强分布规律与重力场中静压强的分 布形式是一样的。H均代表水深 2.a=/2时,即容器沿铅直方向向下或向上作匀加速直线运动,如图213所示,由(231) 可得等压面方程为 g=0 (2-39) 由(2-36)可得压强分布公式为 P=Po+pgH(1-4) (2-40) 二、容器作等角速回转运动 等角速回转的相对平衡原理在工程上有很多应用,如洗衣机、风机、旋风分离器、除尘 器、离心铸造、离心式水泵等。 13
13 a g ) sin (1 ( sin ) ( sin )] sin cos ( sin ) [ cos 0 0 0 g a p gH p g a H a g a g a p p H g a ay y = + − = + − − − − = + − + − − (2-36) 由此可知,当 a,p0 为常数时,液体下面的点的静压强的大小只与液深 H 有关,当斜 面角度变为 0 或/2 时,即可得容器水平或铅直匀加速直线运动的两种特例。 图 2-12 沿水平基面作匀加速直线运动 图 2-13 沿垂直方向作匀加速直线运动 1.=0 时,即容器沿水平基面匀加速运动时,如图 2-12 所示,由(2-31)可得等压面 方程为 tg g a y z = − − = d d (2-37) 由(2-36)可得压强分布公式为 p = p0 + gH (2-38) 此式表明,容器沿水平基面作匀加速运动时的表压强分布规律与重力场中静压强的分 布形式是一样的。H 均代表水深。 2.=/2 时,即容器沿铅直方向向下或向上作匀加速直线运动,如图 2-13 所示,由(2-31) 可得等压面方程为 tg = 0 (2-39) 由(2-36)可得压强分布公式为 (1 ) 0 g a p = p + gH − (2-40) 二、容器作等角速回转运动 等角速回转的相对平衡原理在工程上有很多应用,如洗衣机、风机、旋风分离器、除尘 器、离心铸造、离心式水泵等。 a g y z a z y a
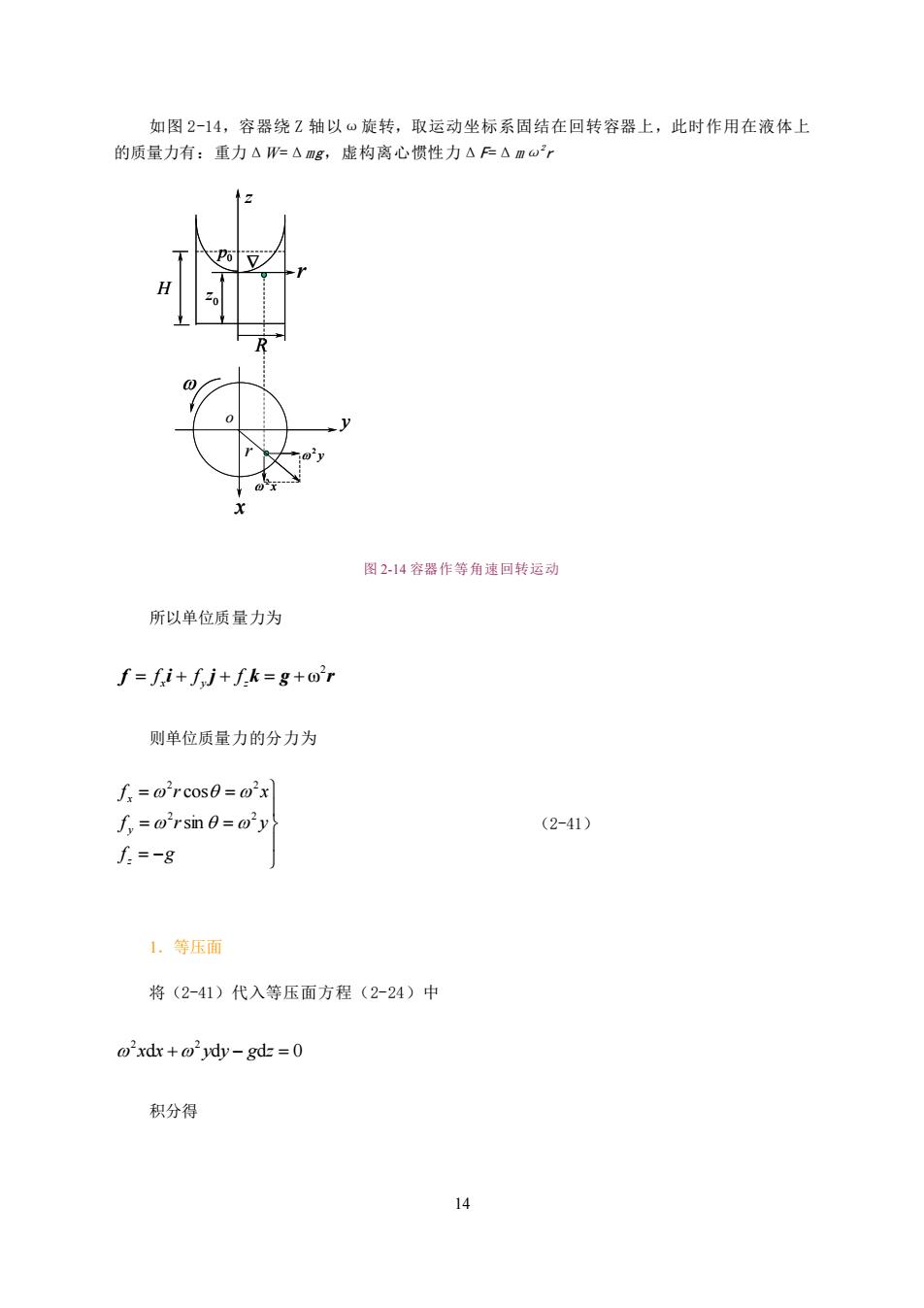
如图2-14,容器绕2轴以。旋转,取运动坐标系固结在回转容器上,此时作用在液体上 的质量力有:重力△形=△mg,虚构离心惯性力△户△mar 图2-14容器作等角速回转运动 所以单位质量力为 f=fi+fj+fk=g+0'r 则单位质量力的分力为 f=@'rcos8=o2x】 f,=o'rsmne=0'y (2-41) 1=-8 1.等压面 将(2-41)代入等压面方程(2-24)中 @'xdx+@'ydy-gd:=0 积分得 14
14 如图 2-14,容器绕 Z 轴以ω旋转,取运动坐标系固结在回转容器上,此时作用在液体上 的质量力有:重力ΔW=Δmg,虚构离心惯性力ΔF=Δmω 2 r 图 2-14 容器作等角速回转运动 所以单位质量力为 f i j k g r 2 = f x + f y + f z = +ω 则单位质量力的分力为 = − = = = = f g f r y f r x z y x 2 2 2 2 sin cos (2-41) 1.等压面 将(2-41)代入等压面方程(2-24)中 d d d 0 2 2 x x + y y − g z = 积分得 x y y 2 x 2 r o r R H z 0 p 0 z x y y 2 x 2 r o r R H z 0 p 0 z