
对于以μm计的小颗粒,常在滞流区沉降。[例4-1]玉米淀粉水悬浮液在20℃时,颗粒的直径为6~21μm,其平均值为15μm,求沉降速度。假定吸水后淀粉颗粒的相对密度为1.02。解:水在20℃时,μ=10-"Pa·s,p=1000kg/m2 ; pp=1020 kg/m2。假定在滞流区沉降,则按斯托克斯公式:_ dp(pp-p)gu.18μ10(02010)98=245x1-m/18×10-3_ 15×10-×2.45×10-×10002 = 3.68×10-5 <1Re, =10-3.u正确,即u,=2.45×10-°m/s。【例 4-2]一直径为15μm,相对密度为0.9的油滴,在21℃,0.1MPa的空气中沉降分离。若沉降时间为2min,试求该油滴沉降分离的高度。解:查附录,得在题设条件下空气的物性为:
对于以μm 计的小颗粒,常在滞流区沉降。 [例 4-1] 玉米淀粉水悬浮液在 20 ℃时, 颗粒的直径为 6~21 μm,其平均值为 15 μ m,求沉降速度。假定吸水后淀粉颗粒的相 对密度为 1.02。 解:水在 20 ℃时,μ=10-3 Pa·s,ρ=1000 kg/m3 ;ρP=1020 kg/m3 。 假定在滞流区沉降,则按斯托克斯公式: sm d g u PP t /1045.2 1018 81.9)10001020()1015( 18 )( 6 3 26 2 − − − ×= × ×−×× = − = μ ρρ 11068.3 10 10001045.21015 Re 5 3 6 6 <×= ×××× = − − − − t ∴ut正确,即 ut=2.45×10-6 m/s。 [例 4-2] 一直径为 15 μm,相对密度为 0.9 的油滴,在 21 ℃,0.1 MPa 的空气中沉 降分离。若沉降时间为 2 min,试求该油滴 沉降分离的高度。 解:查附录,得在题设条件下空气的物性为:

μ=1.8 ×10-s Pa·S, p=1. 20 kg/m假定沉降满足斯托克斯公式:dp(pp-p)gy18μ(15x10)x(900-12)981=6.12×10m/18×1.8×10-5Re15×10*×612x10×12=6.12×1011.8×10-5:.ut正确,即ut=6.12×10-2 m/s。沉降高度:H=ut T =6.12×10- × 2 × 60=0. 734m说明:对于微米级颗粒的沉降,一般在极短的时间内(以毫秒计)就可达到沉降速度,因此可认为,颗粒从一开始就以沉降速度沉降。2.1.2实际沉降速度ut实际的颗粒沉降一般不是自由沉降,且形状也不一定为球形,这时需对u,进行校正。ut' =入,ut入,为校正系数,可参阅式(4-51)~(4-54)。2.1.3重力沉降设备
μ=1.8×10-5 Pa·s,ρ=1.20 kg/m3 假定沉降满足斯托克斯公式: sm d g u PP t /1012.6 108.118 81.9)2.1900()1015( 18 )( 3 5 26 2 − − − ×= ×× ×−×× = − = μ ρρ 11012.6 108.1 2.11012.61015 Re 3 5 6 3 <×= × ×××× = − − − − t ∴ut正确,即 ut=6.12×10-3 m/s。 沉降高度: H=utτ=6.12×10-3×2×60=0.734m 说明:对于微米级颗粒的沉降,一般在极短 的时间内(以毫秒计)就可达到沉降速度, 因此可认为,颗粒从一开始就以沉降速度沉 降。 2.1.2 实际沉降速度ut , 实际的颗粒沉降一般不是自由沉降,且形状 也不一定为球形,这时需对ut进行校正。 ut , =λput λp为校正系数,可参阅式(4-51)~(4-54)。 2.1.3 重力沉降设备
(1) 降尘室如下图所示。KK颗粒被分离下来的条件:颗粒通过降尘室的时间T要等于或大于颗粒沉至器底所需的时间Tt,即:T.>Tt设:L一降尘室的长度,m;H一降尘室的高度,m;B一降尘室宽度,m;ut一颗粒的沉降速度,m/s;u一流体在降尘室中的水平流速,m/s。颗粒在降尘室中的停留时间为:T,=L/u颗粒沉降时间为:T,=H/ut由分离条件,得:L/u≥H/ut将u=q/(HB),可得:
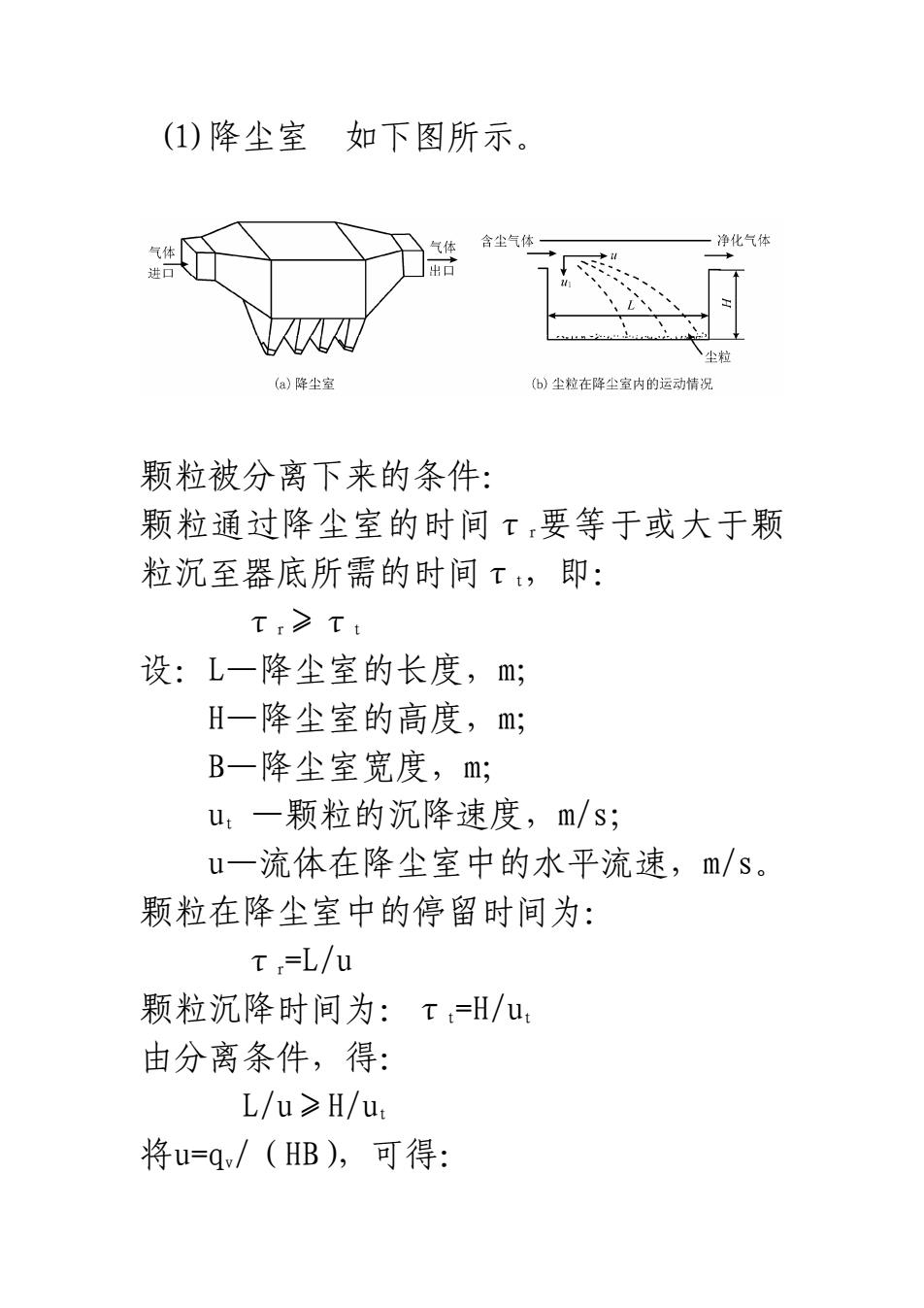
(1)降尘室 如下图所示。 颗粒被分离下来的条件: 颗粒通过降尘室的时间τr要等于或大于颗 粒沉至器底所需的时间τt,即: τr≥τt 设:L—降尘室的长度,m; H—降尘室的高度,m; B—降尘室宽度,m; ut —颗粒的沉降速度,m/s; u—流体在降尘室中的水平流速,m/s。 颗粒在降尘室中的停留时间为: τr=L/u 颗粒沉降时间为:τt=H/ut 由分离条件,得: L/u≥H/ut 将u=qv/(HB),可得:

q<BLu,=Aout式中:q为流体的体积流量,m/s;Ao=BL降尘室的沉降面积,m2。由此可知:降尘室的生产能力只与沉降面积A.及颗粒的沉降速度ut有关,而与降尘室的高度无关,因此,可将降尘室制成多层注意:在计算u,时,要以要求全部被除去的最小颗粒直径计算,且流体速度u要处于滞流范围。(2)连续式沉降器(多尔增浓器)料浆,3H人清液区44 河降1沉淀E颗粒被分离下来的条件:颗粒在沉降器中的沉降速度ut要等于或大于液体的上(或下)流速度u,即:ut≥u
qv≤BLut=A0ut 式中:qv为流体的体积流量,m3 /s; A0=BL降尘室的沉降面积,m2 。 由此可知:降尘室的生产能力只与沉降面积 A0及颗粒的沉降速度ut有关,而与降尘室的 高度无关,因此,可将降尘室制成多层。 注意:在计算ut时,要以要求全部被除去的 最小颗粒直径计算,且流体速度u要处于滞 流范围。 (2)连续式沉降器(多尔增浓器) 颗粒被分离下来的条件: 颗粒在沉降器中的沉降速度ut要等于或大于 液体的上(或下)流速度u,即: ut≥u

设:G一料液中连续相的质量流量,kg/s;Ga一分散相夹带的连续相的质量,kg/s;Ao一沉降面积,m;p一连续相的密度,kg/m。则连续相向上(或下)的流速为:_G-Ga_AG_QU=pApAAo由沉降条件,得:A≥△G/(put )=Q/ut或Q<Aout式中Q为连续相的体积流量,m/s。2.2离心沉降2.2.1分离因数依靠惯性离心力的作用而实现的沉降。分离因数K:同一颗粒所受的离心力与重力之比,即:-rou,=gro"=u,Ku,18μK=@r_2ggrKc的大小是反映离心分离设备性能的重要指标。Kc越大,设备分离效率越高
设:G—料液中连续相的质量流量,kg/s; Gd—分散相夹带的连续相的质量,kg/s; A0—沉降面积,m2 ; ρ—连续相的密度,kg/m3 。 则连续相向上(或下)的流速为: 0 A00 Q A G A GG u d = Δ = − = ρρ 由沉降条件,得: A0≥ΔG/(ρut )=Q/ut 或 Q≤A0ut 式中Q为连续相的体积流量,m3 /s。 2.2 离心沉降 2.2.1 分离因数 依靠惯性离心力的作用而实现的沉降。 分离因数Kc:同一颗粒所受的离心力与重力 之比,即: 2 2 18 )( ω μ ρρ r d u pp r − = tr Ku ct g r uu == 2 ω gr u g r K T c 2 2 == ω Kc 的大小是反映离心分离设备性能的重要 指标。Kc 越大,设备分离效率越高