
电磁场与电磁波 第2章电磁学基本理论 合长K】 (二)电位 1.电位差 电荷9t在电场中受力为:F。=q,E 电荷9t在电场中要保持静止, 需受外力作用为:万。=-q,E 电荷在静电场中由P点移动到A点,外力所做的功为: W=-g.∫E.dl 电位差定义: 单位正电荷由P点移动到A点,外力所做的功称为A点 和P点之间的电位差。 p--了E.d
电磁场与电磁波 第2章 电磁学基本理论 (二)电位 电荷 qt 在电场中受力为: F q E e t Fe F a F q E a t 电荷在静电场中由P点移动到A点,外力所做的功为: t d A P W q E l 电位差定义: 单位正电荷由P点移动到A点,外力所做的功称为A点 和P点之间的电位差。 1. 电位差 t d A AP P W E l q 电荷 在电场中要保持静止, 需受外力作用为: qt

电磁场与电磁波 第2章电磁学基本理论 合长K 例3:计算原点处一点电荷q产生的电场中AP之间的电位差。 解:选取求坐标系,点电荷q产生的电场 E=. pr=-∫E.d7 y dT =drag+Rdodp+Rsinedpa 所以e=ji是月a.da -品京 结论: 空间两点的电位差只 与两点所在位置有关, 而与积分路径无关
电磁场与电磁波 第2章 电磁学基本理论 d A AP P E l d d d sin d ˆ ˆ ˆ R l Ra R a R a 2 0 2 0 1 ˆ d ˆ 4π 1 d 4π P A P AP R R A R R q a Ra R q R R 0 1 1 4π A P q R R 结论: 空间两点的电位差只 与两点所在位置有关, 而与积分路径无关。 例3:计算原点处一点电荷q 产生的电场中AP之间的电位差。 2 0 1 ˆ 4π R q E a R 解:选取求坐标系,点电荷q 产生的电场 所以: x y z P A o

电磁场与电磁波 第2章电磁学基本理论 合长K 2.电位 (1)电位定义: 外力将单位正电荷是由无穷远处移到A点,则A点和 无穷远处的电位差称为A点的电位。 .-八E山4品反 91 以无穷远处为零电位参考点。R4为电荷源到A点的距离。 (2)电位计算: a.点电荷的电位计算:中= 4π8R 多个点电荷的电位计算:中= 其中:R,为第个电荷源到A点的距离
电磁场与电磁波 第2章 电磁学基本理论 (1)电位定义: 外力将单位正电荷是由无穷远处移到A点,则A点和 无穷远处的电位差称为A点的电位。 2. 电位 0 1 d 4π A A A q E l R 以无穷远处为零电位参考点。 RA 为电荷源到A点的距离。 (2)电位计算: a.点电荷的电位计算: 0 4π q R 多个点电荷的电位计算: 其中: R i 为第i个电荷源到A点的距离。 0 1 1 4π N i i i q R

电磁场与电磁波 第2章电磁学基本理论 合长K】 b.连续分布的电荷源的电位计算 线电荷分布:-4记忘会r 面电荷分布:。=G,贵a5 体电荷分布:中= 货 3.电场强度E与电位中之间的关系 =-JE-d7 do=-E.dl d中=Vb.di → E=-V中
电磁场与电磁波 第2章 电磁学基本理论 0 1 d 4π V V V R b.连续分布的电荷源的电位计算 线电荷分布: 面电荷分布: 体电荷分布: d l E l d d E l d d l E 3. 电场强度 E 与电位 之间的关系 0 1 d 4π S S S R 0 1 d 4π l l l R
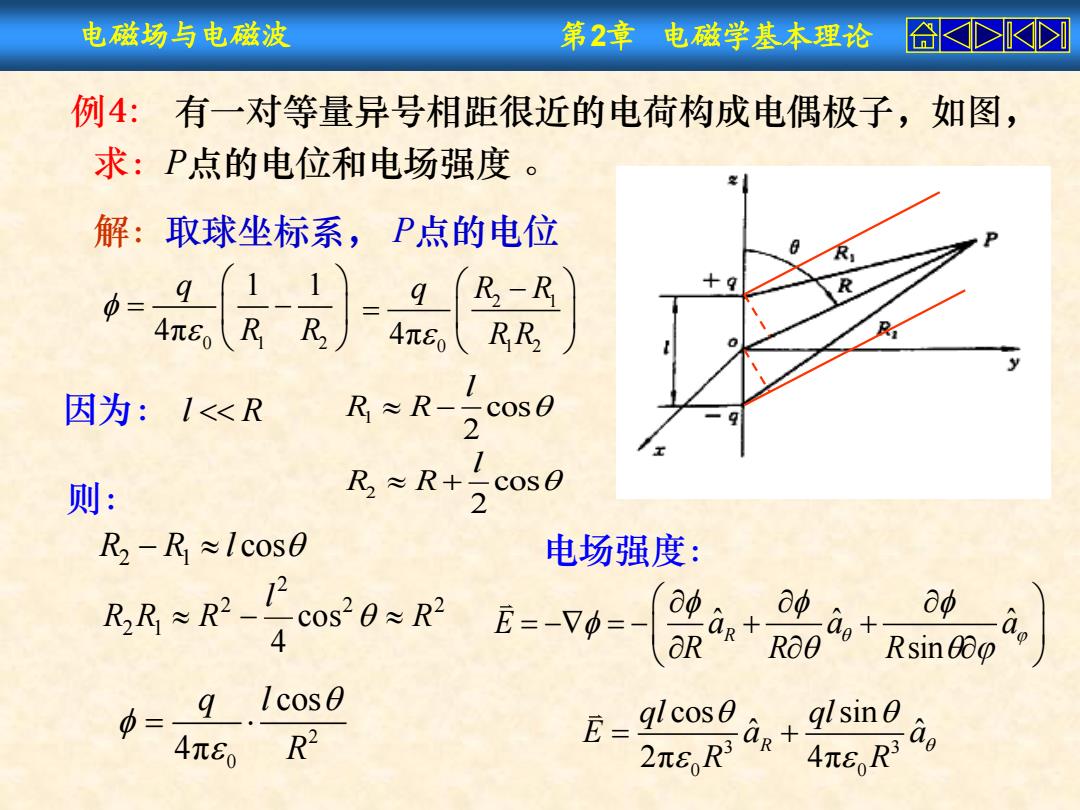
电磁场与电磁波 第2章电磁学基本理论 合长KI 例4:有一对等量异号相距很近的电荷构成电偶极子,如图, 求:P点的电位和电场强度 解:取球坐标系,P点的电位 R-R R RR 因为:1<R R≈R-5cos0 2 则: R≈R+5cosB 2 R2-R,≈Icos0 电场强度: R2-c00R & 8o 4 E=-V0=- aR R60 Rsin 9 Icos0 ql cosθ glsin 4π80 R2 E 2πERae+ 4π8,R
电磁场与电磁波 第2章 电磁学基本理论 例4: 有一对等量异号相距很近的电荷构成电偶极子,如图, 求:P点的电位和电场强度 。 解:取球坐标系, P点的电位 因为: l R 1 cos 2 l R R R2 R1 l cos 2 2 2 2 2 1 cos 4 R l R R R 2 cos 2 l R R 则: 电场强度: ˆ ˆ ˆ sin E a a a R R R R 3 3 0 0 cos sin ˆ ˆ 2π 4π R ql ql E a a R R 0 1 2 1 1 4π q R R 2 1 0 1 2 4π q R R R R 2 0 cos 4π q l R