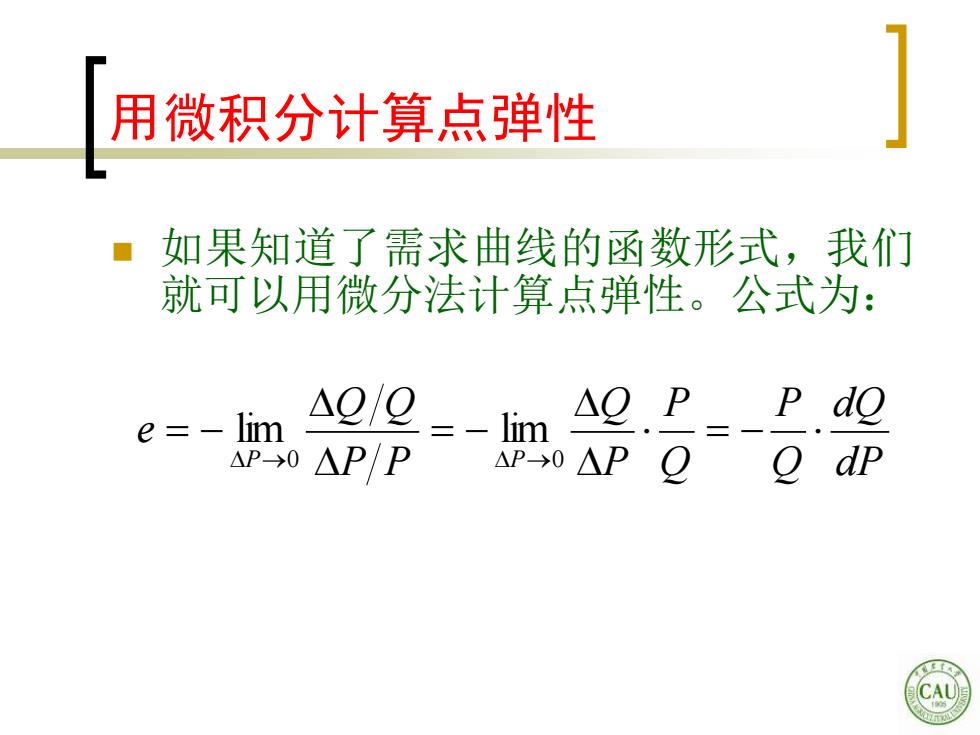
用微积分计算点弹性 如果知道了需求曲线的函数形式,我们 就可以用微分法计算点弹性。公式为: e=-lim △Q/Q lim A.P=- P do AP0△P/P AP→0△PQ o dp CAU
用微积分计算点弹性 ◼ 如果知道了需求曲线的函数形式,我们 就可以用微分法计算点弹性。公式为: dP dQ Q P Q P P Q P P Q Q e P P = − = − = − →0 →0 lim lim

例题: 已知某种商品需求函数为Q=20-2p,导 出点弹性公式,并计算P=2和P=6时的点 弹性。 2P e=- P do o dp 22 ■当P=2时,Q=20-2×2=16∴.e=2×2/16=0.25 当P=6时,Q=20-2×6=8∴.e=2×6/8=1.5 CAU
例题: ◼ 已知某种商品需求函数为Q=20-2p,导 出点弹性公式,并计算P=2和P=6时的点 弹性。 ◼ 当P=2时,Q=20-2×2=16 ∴e=2×2/16=0.25 ◼ 当P=6时,Q=20-2×6=8 ∴e=2×6/8=1.5 Q P Q P dP dQ Q P e 2 = − = − (−2) =

三、需求价格弹性的类型 ■1、完全有弹性e=o∝ D Q 思考:哪些商品具有完全弹性? CAU
◼ 1、完全有弹性 e=∝ 三、需求价格弹性的类型 P Q D 思考:哪些商品具有完全弹性?

三、需求价格弹性的类型 ■2、完全无弹性e=0 Q 思考:哪些商品具有完全无弹性? CAU
◼ 2、完全无弹性 e=0 三、需求价格弹性的类型 P Q D 思考:哪些商品具有完全无弹性?

三、需求价格弹性的类型 ■3、单位弹性e=1 D 思考:哪些商品具有单位弹性? CAU
◼ 3、单位弹性 e=1 三、需求价格弹性的类型 P Q D 思考:哪些商品具有单位弹性?