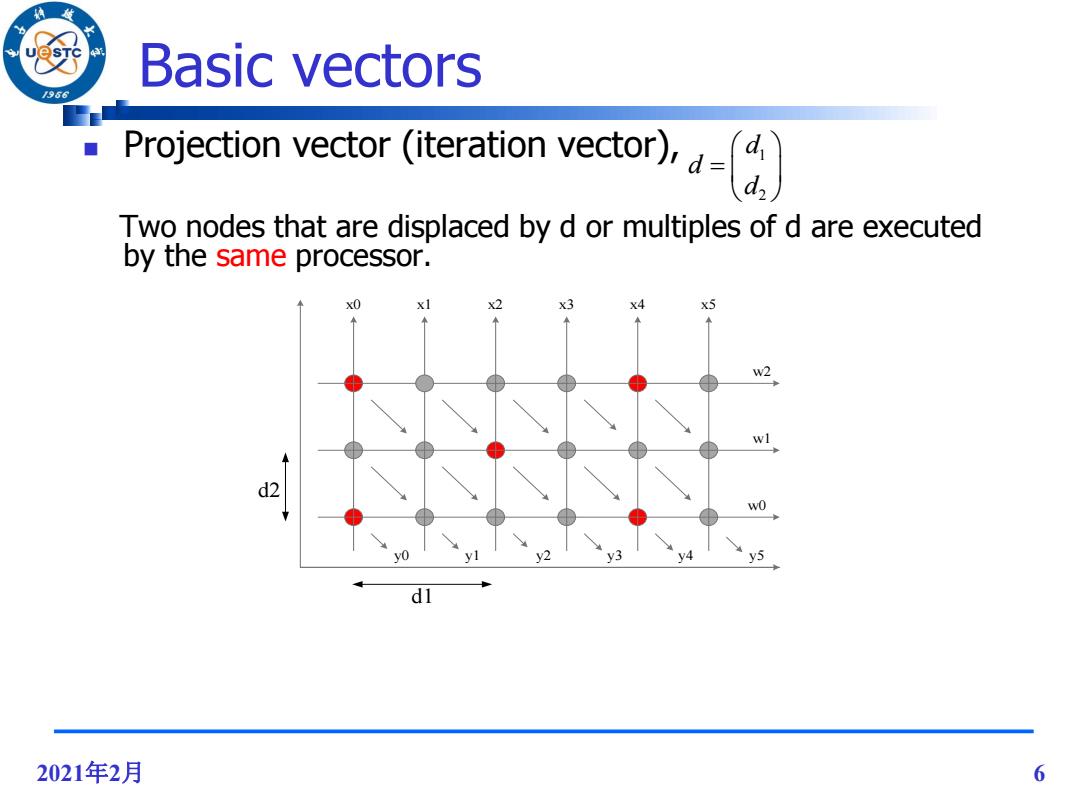
Basic vectors 966 Projection vector (iteration vector), d= 4 Two nodes that are displaced by d or multiples of d are executed by the same processor. x0 xI x2 x3 x4 5 w2 wl d2 y2 y5 2021年2月 6
2021年2月 6 Basic vectors Projection vector (iteration vector), Two nodes that are displaced by d or multiples of d are executed by the same processor. 1 2 d d d x0 x1 x2 x3 x4 x5 y0 y1 y2 y3 y4 y5 w0 w2 w1 d2 d1

Basic vectors 96 Processor space vector,p= P P2 any node with index IT=(i j)would be executed by processor -n Scheduling vector, S= Space rotation S2」 Any node with index I would be executed at time sTI s1=(s Hardware Utilization Efficiency,HUE=1/IsTdl. This is because two tasks executed by the same processor are spaced |sd|time units apart. 2021年2月 7
2021年2月 7 Basic vectors Processor space vector, any node with index IT=(i j) would be executed by processor Scheduling vector, Any node with index I would be executed at time sT I. Hardware Utilization Efficiency, HUE=1/|sTd|. This is because two tasks executed by the same processor are spaced |sTd| time units apart. 1 2 s s s Space rotation 1 2 p p p 1 2 ( ) T i p I p p j 1 2 ( ) T i s I s s j

Feasibility constraints /96 Processor space vector and projection vector must be orthogonal to each other. p d=0 If node A and B differ by d,they must be executed by the same processor. If A and B are mapped to the same processor,then they cannot be executed at the same time,i.e. sTd≠0 Edge mapping:If an edge e exists in the space representation or DG,then an edge pe is introduced in the systolic array with se delays. 2021年2月 8
2021年2月 8 Feasibility constraints Processor space vector and projection vector must be orthogonal to each other. p Td=0 If node A and B differ by d, they must be executed by the same processor. If A and B are mapped to the same processor, then they cannot be executed at the same time, i.e. s Td0 Edge mapping: If an edge e exists in the space representation or DG, then an edge pTe is introduced in the systolic array with sTe delays

definitions 96 A DG can be transformed to a space-time representation by interpreting one of the spatial dimensions as temporal dimension(时间维度). For a 2-D DG,the general transformation is described by i'=t=0,j'=p I,and t'=sTI,i.e. j':processor axis t':scheduling time instance 2021年2月 9
2021年2月 9 definitions A DG can be transformed to a space-time representation by interpreting one of the spatial dimensions as temporal dimension(时间维度). For a 2-D DG, the general transformation is described by i’=t=0, j’=pT I, and t’=sT I, i.e. j’ : processor axis t’ : scheduling time instance

7.3 FIR systolic arrays /96 7.3.1 Design B(Broadcast Inputs,Move Results,Weights Stay) How to Selecting dT=(1 0),pT=(0 1),sT=(1 0) select sT? refer to 7.4. Any node with index IT=(i j) is mapped to processor plI=j. all nodes on horizontal line are mapped to the same processor. is executed at time sI=i. Since s'd=1,we have HUE=1/s'd=1
7.3 FIR systolic arrays 7.3.1 Design B1 (Broadcast Inputs, Move Results, Weights Stay) Selecting dT=(1 0), pT=(0 1), sT=(1 0) Any node with index IT=(i j) is mapped to processor pT I=j. all nodes on horizontal line are mapped to the same processor. is executed at time sT I=i. Since sTd=1, we have HUE=1/|sTd|=1. How to select sT? refer to 7.4