
教案第十九章量子物理 即:电子在核外作圆周运动的半径由(3)式决定,n=1时可得:=529×1"m=0.53A, 是H原子核外最小的轨道半径,也称Bor半径。 这个数值与用其它方法得到的数值符合的很好。 能量的计算: E=静电能+电子动能:∞外为静电能0点 则:E,=m4E e2 代入上式得: 由假设(2)知:,=m7. e2 一然代入可得: e2 n=1,2,3…(4) 由(4)式知,核外电子的能量是量子化的,这种能量称为能级。 N=1时,E1=-13.6CV:称为H原子的基态。 这个数据与实验测得的H原子的电离电势能符合的很好。 (解释电离能的概念) >1的各能量状态称为受激态。 4里德伯(J.R.Rydbeng)公式的推导: 由Bohr的第三条假设可推得Rydbeng公式: hy=E,-E y=E,-E 7-5 ) 8cC=1.097373x10'm me* R Rp=1.096776×10'm
教案 第十九章 量子物理 328 即:电子在核外作圆周运动的半径由(3)式决定,n=1 时可得: 11 1 5.29 1 − = m=0.53Å, 是 H 原子核外最小的轨道半径,也称 Bohr 半径。 这个数值与用其它方法得到的数值符合的很好。 能量的计算: E=静电能+电子动能;外为静电能 O 点 则: n n n e E mv 0 2 2 2 4 1 = − 由假设(2)知: n n m h v = 代入上式得: n n n e m n E 0 2 2 2 2 2 4 = − ; 2 2 0 me h n = 代入可得: n n e h n me E 0 2 2 2 2 0 4 8 1 8 = − = − n=1,2,3…… (4) 由(4)式知,核外电子的能量是量子化的,这种能量称为能级。 N=1 时,E1=-13.6eV;称为 H 原子的基态。 这个数据与实验测得的 H 原子的电离电势能符合的很好。 (解释电离能的概念) n>1 的各能量状态称为受激态。 4 里德伯(J.R.Rydbeng)公式的推导: 由 Bohr 的第三条假设可推得 Rydbeng 公式: h = En − Ek h En − Ek = = − = − − = = 2 2 2 3 2 2 0 4 1 1 1 1 8 ~ k n R h C k n me hC E E C n k * 7 1 2 3 0 4 1.097373 10 8 − = = m h C me R 7 1 exp 1.096776 10 − R = m
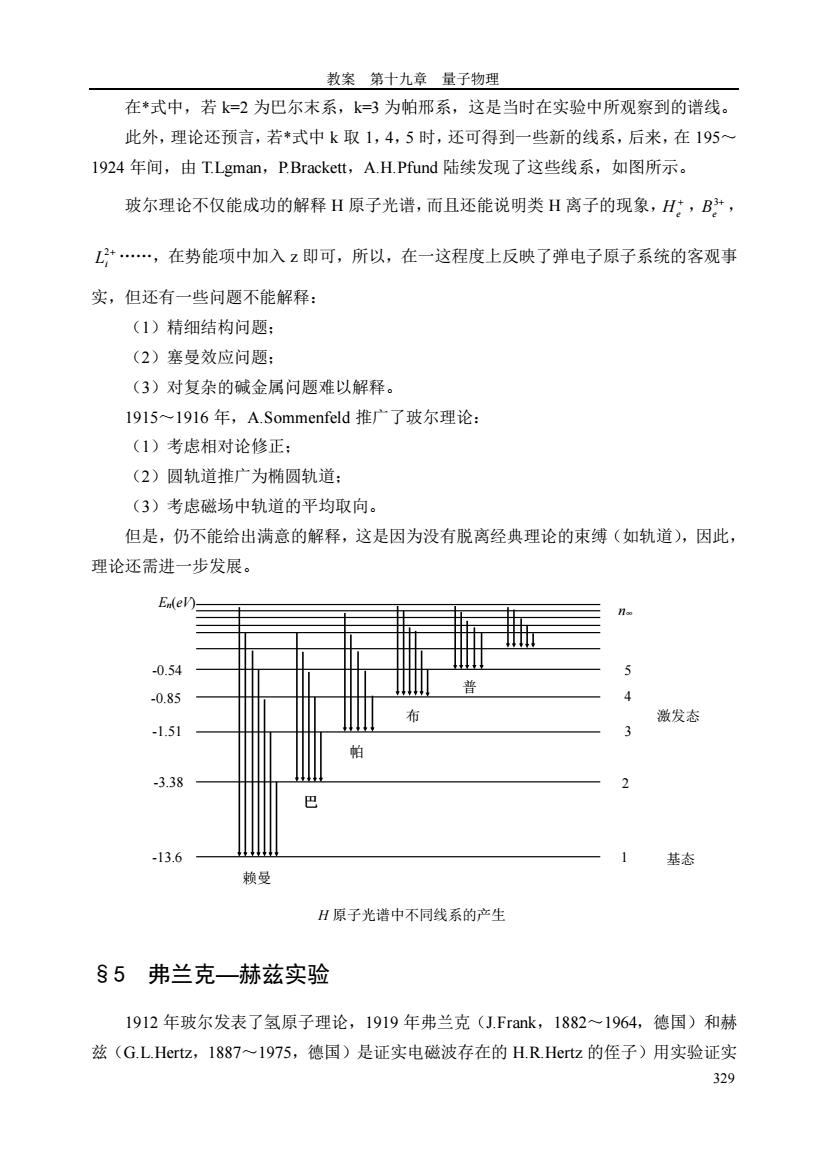
教案第十九章量子物理 在*式中,若k=2为巴尔末系,k=3为帕邢系,这是当时在实验中所观察到的谱线。 此外,理论还预言,若*式中k取1,4,5时,还可得到一些新的线系,后来,在195 1924年间,由TLgman,P.Brackett,,A.H.Pfund陆续发现了这些线系,如图所示。 玻尔理论不仅能成功的解释H原子光谱,而且还能说明类H离子的现象,H;,B”, …,在势能项中加入z即可,所以,在一这程度上反映了弹电子原子系统的客观事 实,但还有一些问题不能解释: (1)精细结构问题: (2)塞曼效应问题 (3)对复杂的碱金属问题难以解释, 1915~1916年,A.Sommenfeld推广了玻尔理论: (1)考虑相对论修正: (2)圆轨道推广为椭圆轨道: (3)考虑磁场中轨道的平均取向。 但是,仍不能给出满意的解释,这是因为没有脱离经典理论的束缚(如轨道),因此 理论还需进一步发展。 E(eV- -0.54 -0.85 激发态 -1.51 -338 巴 -13.6 基态 赖曼 H原子光谱中不同线系的产生 §5弗兰克一赫兹实验 1912年玻尔发表了氢原子理论,1919年弗兰克(J.Frak,1882~1964,德国)和赫 兹(G.L.Hertz,1887~1975,德国)是证实电磁波存在的H.R.Hert立的侄子)用实验证实 329
教案 第十九章 量子物理 329 在*式中,若 k=2 为巴尔末系,k=3 为帕邢系,这是当时在实验中所观察到的谱线。 此外,理论还预言,若*式中 k 取 1,4,5 时,还可得到一些新的线系,后来,在 195~ 1924 年间,由 T.Lgman,P.Brackett,A.H.Pfund 陆续发现了这些线系,如图所示。 玻尔理论不仅能成功的解释 H 原子光谱,而且还能说明类 H 离子的现象, + He , 3+ Be , 2+ Li ……,在势能项中加入 z 即可,所以,在一这程度上反映了弹电子原子系统的客观事 实,但还有一些问题不能解释: (1)精细结构问题; (2)塞曼效应问题; (3)对复杂的碱金属问题难以解释。 1915~1916 年,A.Sommenfeld 推广了玻尔理论: (1)考虑相对论修正; (2)圆轨道推广为椭圆轨道; (3)考虑磁场中轨道的平均取向。 但是,仍不能给出满意的解释,这是因为没有脱离经典理论的束缚(如轨道),因此, 理论还需进一步发展。 §5 弗兰克—赫兹实验 1912 年玻尔发表了氢原子理论,1919 年弗兰克(J.Frank,1882~1964,德国)和赫 兹(G.L.Hertz,1887~1975,德国)是证实电磁波存在的 H.R.Hertz 的侄子)用实验证实 En(eV) -0.54 -0.85 -1.51 -3.38 -13.6 1 2 3 4 5 n∞ 赖曼 巴 帕 布 普 基态 激发态 H 原子光谱中不同线系的产生

教案第十九章量子物理 了原子能级,示意图如下: 玻璃管B内为低压水银蒸汽,电子从加热的灯丝F发射出来,在加速电压Uo下被加 速,在栅极G和P之间有一个小的反向电压U=0.5V,电子到达P后,可在电路中观察 到板极电流P。实验结果如图所示,电流是有峰极的。 设汞原子基态能量为E1,第一激发态能量为E2,Ek为加速电子的动能。若Ek<E2-E1, 装置示意图 实验数据图 则电子不能使汞原子激发,电子动能无损失,1p也随U6增加,当EkE2-E1时,在碰撞中 汞原子从电子中吸收EE,的能量跃迁到激发态,故电子动能由于碰撞而减少,p亦急刷 的降低,这就对应图中第一个波谷,若电子连续与两个汞原子碰撞,使两个汞原子跃迁 到激发态,则会出现第二个波谷,余此类推。 因峰值之间的电压为49V,故4.9V为汞原子第一激发态与基态间能量差 E2-E1=4.9eV,4.9V称为汞原子的第一激发电势。 处于激发成的汞原子跃迁到基态时,要发射光子,其波长为: hy=E2-E =E0-24x10am 在实验中确实能观察到此谱线。 弗兰克一赫兹实验证明,原子能级确定存在的,他们二位科学家因此而获1925年诺 贝尔物理学奖。 §6德布罗意波、实物粒子的二象性de Broglie Wave,matter wave 1.德布罗意假设 德布罗意根据对光的性质的认识,提出实物粒子也具有波粒二象性。 330
教案 第十九章 量子物理 330 了原子能级,示意图如下: 玻璃管 B 内为低压水银蒸汽,电子从加热的灯丝 F 发射出来,在加速电压 U0 下被加 速,在栅极 G 和 P 之间有一个小的反向电压 Ur=0.5V,电子到达 P 后,可在电路中观察 到板极电流 IP。实验结果如图所示,电流是有峰极的。 设汞原子基态能量为 E1,第一激发态能量为 E2,Ek 为加速电子的动能。若Ek<E2-E1, 则电子不能使汞原子激发,电子动能无损失,IP也随 U0 增加,当 EkE2-E1 时,在碰撞中 汞原子从电子中吸收 E2-E1 的能量跃迁到激发态,故电子动能由于碰撞而减少,IP亦急剧 的降低,这就对应图中第一个波谷,若电子连续与两个汞原子碰撞,使两个汞原子跃迁 到激发态,则会出现第二个波谷,余此类推。 因峰值之间的电压为 4.9V,故 4.9eV 为汞原子第一激发态与基态间能量差 E2-E1=4.9eV,4.9V 称为汞原子的第一激发电势。 处于激发成的汞原子跃迁到基态时,要发射光子,其波长为: h = E2 − E1 nm E E Ch 2 2 1 = 2.54 10 − = 在实验中确实能观察到此谱线。 弗兰克—赫兹实验证明,原子能级确定存在的,他们二位科学家因此而获 1925 年诺 贝尔物理学奖。 §6 德布罗意波、实物粒子的二象性 de Broglie Wave, matter wave 1.德布罗意假设 德布罗意根据对光的性质的认识,提出实物粒子也具有波粒二象性。 B F e‐ e‐ U1 U2 G P IP U0 IP 装置示意图 实验数据图