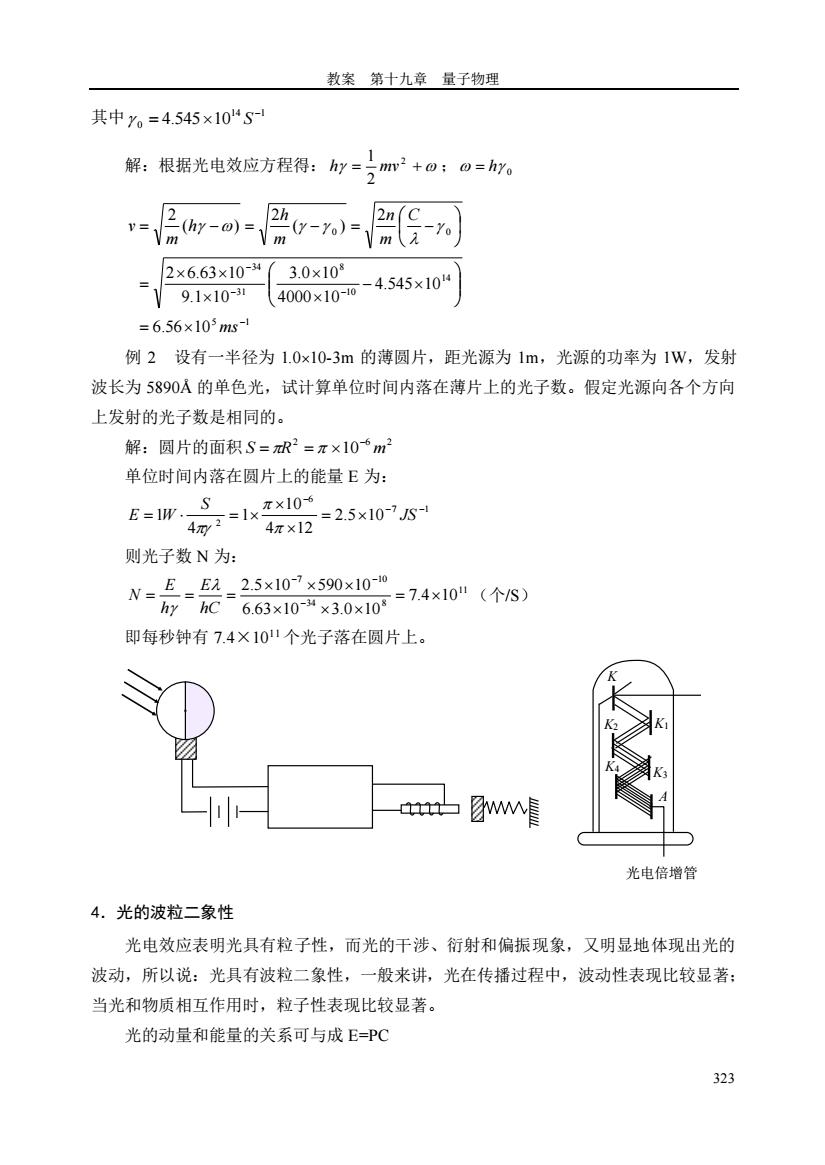
教案第十九章量子物理 其中。=4.545×10“S 解:根据光电效应方程得:r=m2+o:o=hr。 2x6.63×10- 3.0×10 =9.1x100 4000×10-H0 -4.545x104 =6.56×103ms 例2设有一半径为1.0x10-3m的薄圆片,距光源为1m,光源的功率为1W,发射 波长为5890A的单色光,试计算单位时间内落在薄片上的光子数。假定光源向各个方向 上发射的光子数是相同的: 解:圆片的面积S=R2=π×10‘m 单位时间内落在圆片上的能量E为: π×106 =2.5×10-7JS- 则光子数N为: -号-是-名0o-140个 即每秒钟有7.4×101个光子落在圆片上。 m白☑M虐 光电倍增管 4.光的波粒二象性 光电效应表明光具有粒子性,而光的干涉、衍射和偏振现象,又明显地体现出光的 波动,所以说:光具有波粒二象性,一般来讲,光在传播过程中,波动性表现比较显著: 当光和物质相互作用时,粒子性表现比较显著。 光的动量和能量的关系可与成E=PC 323
教案 第十九章 量子物理 323 其中 14 1 0 4.545 10 − = S 解:根据光电效应方程得: = + 2 2 1 h mv ; 0 = h 5 1 14 10 8 31 34 0 0 6.56 10 4.545 10 4000 10 3.0 10 9.1 10 2 6.63 10 2 ( ) 2 ( ) 2 − − − − = − = = − = − = − ms C m n m h h m v 例 2 设有一半径为 1.010-3m 的薄圆片,距光源为 1m,光源的功率为 1W,发射 波长为 5890Å 的单色光,试计算单位时间内落在薄片上的光子数。假定光源向各个方向 上发射的光子数是相同的。 解:圆片的面积 2 6 2 S R 10 m − = = 单位时间内落在圆片上的能量 E 为: 7 1 6 2 2.5 10 4 12 10 1 4 1 − − − = = = JS S E W 则光子数 N 为: 11 34 8 7 10 7.4 10 6.63 10 3.0 10 2.5 10 590 10 = = = = − − − hC E h E N (个/S) 即每秒钟有 7.4×1011 个光子落在圆片上。 4.光的波粒二象性 光电效应表明光具有粒子性,而光的干涉、衍射和偏振现象,又明显地体现出光的 波动,所以说:光具有波粒二象性,一般来讲,光在传播过程中,波动性表现比较显著; 当光和物质相互作用时,粒子性表现比较显著。 光的动量和能量的关系可与成 E=PC K K2 K4 K1 K3 A 光电倍增管

教案第十九章量子物理 P名9 即:H=:P=号 上式可以看出,光的粒子性描述量E和P通过普朗克常数h和描述光的波动性的量) 和y联系在起,故通常把h称为作用量子。 §3康普顿效应Compton Effect 1922~23年间,康普顿(AH.Compton)研究院x射线经金属、石墨等物质的散射 现象,实验结果指出:散射分式中有与入射波长相同的波线,也有大于入射波波长的射 线,这种改变波长的散射称为康普顿效应,波长的改变△随散射角而异,当散射角增加 时,波长的改变也随之增加。 入射线 60 090 X射线源 射谱仪 实验示意图 实验结果图 按经典理论,散射波的频率与入射光的频率相同,解释不了康普顿效庆。 如果应用光子概念,假设光子和实物粒子一样,能与电子等粒子发生弹性碰撞,即 可解释康普顿效应,因为:碰撞时,光子的能量?给电子,故散射波的波长变长。 康普顿效应不仅有力的证实了光子假设的正确性,而且证实了在微观粒子的相互作 用过程中,也严格的遵守能量守恒和动量守恒。 康普顿效应的推导: 如图:碰撞时动量、能量守恒: (hwle)n hyo+moC2 =hy +mc2 (1) h
教案 第十九章 量子物理 324 h C h C E P = = = 即: H = h ; h P = 上式可以看出,光的粒子性描述量 E 和 P 通过普朗克常数 h 和描述光的波动性的量 和联系在起,故通常把 h 称为作用量子。 §3 康普顿效应 Compton Effect 1922~23 年间,康普顿(A.H.Compton)研究院 x 射线经金属、石墨等物质的散射 现象,实验结果指出:散射分式中有与入射波长相同的波线,也有大于入射波波长的射 线,这种改变波长的散射称为康普顿效应,波长的改变随散射角而异,当散射角增加 时,波长的改变也随之增加。 按经典理论,散射波的频率与入射光的频率相同,解释不了康普顿效庆。 如果应用光子概念,假设光子和实物粒子一样,能与电子等粒子发生弹性碰撞,即 可解释康普顿效应,因为:碰撞时,光子的能量?给电子,故散射波的波长变长。 康普顿效应不仅有力的证实了光子假设的正确性,而且证实了在微观粒子的相互作 用过程中,也严格的遵守能量守恒和动量守恒。 康普顿效应的推导: 如图:碰撞时动量、能量守恒: 2 2 h 0 + m0C = h + mC (1) 光阑 X 射线源 0 散射物质 射谱仪 实验示意图 0 入射线 =0 =45 =90 =135 实验结果图 (h0/c)n (h0/c)n0 mv x

教案第十九章量子物理 处元,-g万+m 动量守恒方程可写为:(余弦定理): om-2-竖名w 即:m2v2C2=y6+y2-2h2 Yoycos6 (2) 将(1)式平方减去(2)式得: mcca-co)mc 化为:C,-2.h0-c0s Yor moc 操后写房-大染n号 (3) 由(3)式可以看出,波长改变与散射物质无关,仅决定于散射方向,当散射角增 大时,0也将随之增加,并且-.0的理论值也能与实验结果相结合。 (3)式中h叫康普顿波长,是一个常数: 6.63×10-4 即:C2n1i03x10=24x10m=0243A 由(3)式可以看出,波长的改变量与入射光的波长无关,对于波长较长的可见光, 波长的政支量A与入射光的波长相比小得多。例如:10m的微流,兰-243×10。 因此观察不到康普顿效应,这时量子结果与经典结果是一致的。而对=1A 兰-20:这时才能发察到康额效应。这种情况下,经真结果就失效了。 例题:设波长入,=1.00×10~°m的x射线与自由电子弹性碰撞,散射角0=90°,问 (1)散射波长的改变是A为多少? (2)反冲电子得到多少动能? (3)在碰撞中,光子能量损失了多少? 解:)根据公式有:△2=h (-cos0) 6.63×10-34 甲A以=21n0×3000-ecos909)=243x10-9m 名
教案 第十九章 量子物理 325 n mv C h n C h = + 0 0 动量守恒方程可写为:(余弦定理): ( ) 2 cos 0 2 2 2 0 C h C h C h C h mv − + = 即: 2 0 cos 2 2 2 2 0 2 2 2 2 m v C = h + h − h (2) 将(1)式平方减去(2)式得: 1 2 (1 cos ) 2 ( ) 0 2 0 0 2 4 2 2 0 2 2 4 = − − + − − m C h m C h C v m C 化为: (1 cos ) ( ) 0 0 0 = − − m C C h 最后写为: 2 sin 2 2 0 0 m C h − = (3) 由(3)式可以看出,波长改变与散射物质无关,仅决定于散射方向,当散射角增 大时,-0 也将随之增加,并且-0 的理论值也能与实验结果相结合。 (3)式中 m C h 0 叫康普顿波长,是一个常数: 即: 2.43 10 0.0243 9.11 10 3 10 6.63 10 12 31 4 34 0 = = = − − − m m C h Å; 由(3)式可以看出,波长的改变量与入射光的波长无关,对于波长较长的可见光, 波长的改变量与入射光的波长相比小得多。例如:=10cm 的微波, 11 2.43 10 − = , 因此观察不 到康普 顿效应, 这时量子 结果与 经典结果 是一致 的。而对 =1Å, 2 2.43 10 − = ;这时才能观察到康普顿效应,这种情况下,经典结果就失效了。 例题:设波长 10 0 1.00 10− = m 的 x 射线与自由电子弹性碰撞,散射角=90,问 (1)散射波长的改变是为多少? (2)反冲电子得到多少动能? (3)在碰撞中,光子能量损失了多少? 解:(1)根据公式有: (1 cos ) 0 = − m C h 即 m 12 31 8 34 (1 cos90 ) 2.43 10 9.11 10 3.0 0 6.63 10 − − − − = =

教案第十九章量子物理 (2)根据能量守恒有:mC2-m,C2=hy。-h似 即: E=。-=ChC 入。1 1 =d+a hC△M =+△网 =295eV (3)因为能量守恒,光子损失的能量等于反冲电子获得的动能 s4氢原子的玻耳理论Bohr Hydrogence-一atomic Theory 1.原子光谱的实验规律: 1讲述原子光谱的作用和用途 H原子光谱: 巴乐末(J.Balmer)经验公式:由实验数据总结得出: =8657A:m3.45 1 R=音=1.09676×P'm称为里德伯常数(Rydbeng) 2里兹合并原理(W.Ritz) 碱金属:氵=Tk)-Tm) Tk)、Tn)称为光谱项 R 7k+aTn+所 iim 1 H原子的帕邢系(F.Paschen): 7一仔习:这他是由实验意结出的公式
教案 第十九章 量子物理 326 (2)根据能量守恒有: mC − m C = h − h 0 2 0 2 即: eV hC hC hC hC E h h k 295 ( ) 1 1 0 0 0 0 0 0 = + = + = + = − = − (3)因为能量守恒,光子损失的能量等于反冲电子获得的动能。 §4 氢原子的玻耳理论 Bohr Hydrogence-atomic Theory 1.原子光谱的实验规律: 1 讲述原子光谱的作用和用途 H 原子光谱: 巴乐末(JJ.Balmer)经验公式:由实验数据总结得出: 4 2 2 − = n n B ;B=3645.7Å;n=3,4,5…… = − = − − = = 2 2 2 2 2 2 1 2 1 1 2 4 4 1 n RC B n C C Bn C n 或: = = − 2 2 1 2 ~ 1 1 n R 7 1 1.096776 1 4 − − = = m B R 称为里德伯常数(Rydbeng) 2 里兹合并原理(W.Ritz) 碱金属: ( ) ( ) ~ = T k −T n T(k)、T(n)称为光谱项 2 ( +) = k R Tk ; 2 ( + ) = n R Tn 即: + − + = 2 2 ( ) 1 ( ) ~ 1 k n R H 原子的帕邢系(F.Paschen): = − 2 2 1 3 ~ 1 n R ;这也是由实验总结出的公式

教案第十九章量子物理 根据大量的实验数据,总结出H原子的光谱有如下规律: (1)波数由两个谱项的差值决定。 (2)前项决定以后,后项取不同值,可给出同一线系中不同谱线的波数。 (3)改变前项的值,可给出不同的线系。 对于这些现象,当时只停留在实验阶段,不能给出满意的理论解释。 2.卢瑟福的原子核模型 原子的核型结构 19Il年,E.Ruthenford在x粒子散射实验的基础上,提出了原子的核型结构的理论, 如下图: 缺点:①按经典理论,由于在核外做变速圆周运动时 应以辐射电磁波的形式向外辐射能量,与圆周运动的频率 核外由子 相对应,电磁波也是这一频率,这样,能量将逐渐减小 从而频率改变,光谱应是连续的,而实验并非如此:②电 子半径逐渐减少,最后将落后在原子核上,这也与实验不 符。 这是经典理论所面临的困难,怎样解决这个困难是比较重要的课题,1913年,玻尔 提出大胆的假设。 3.氢原子的玻耳理论 1玻尔理论的基本假设:(当时是针对H原子提出的) ①能量是量子化的,处于稳定态的原子的电子,绕核作圆周运动,但不辐射能量, ②轨道是量子化的,其矩L=名:=1.2n为量子致 ③电子跃迁时,发射或吸收能量为:hy=E。-E, 2H原子轨道半径和能量的计算 根聚牛锁定排有号 2 (1) 又由假设(2):L=my=nh (2) e1,2,3
教案 第十九章 量子物理 327 根据大量的实验数据,总结出 H 原子的光谱有如下规律: (1)波数由两个谱项的差值决定。 (2)前项决定以后,后项取不同值,可给出同一线系中不同谱线的波数。 (3)改变前项的值,可给出不同的线系。 对于这些现象,当时只停留在实验阶段,不能给出满意的理论解释。 2.卢瑟福的原子核模型 原子的核型结构 1911 年,E.Ruthenford 在 x 粒子散射实验的基础上,提出了原子的核型结构的理论, 如下图: 缺点:①按经典理论,由于在核外做变速圆周运动时, 应以辐射电磁波的形式向外辐射能量,与圆周运动的频率 相对应,电磁波也是这一频率,这样,能量将逐渐减小, 从而频率改变,光谱应是连续的,而实验并非如此;②电 子半径逐渐减少,最后将落后在原子核上,这也与实验不 符。 这是经典理论所面临的困难,怎样解决这个困难是比较重要的课题,1913 年,玻尔 提出大胆的假设。 3.氢原子的玻耳理论 1 玻尔理论的基本假设:(当时是针对 H 原子提出的) ①能量是量子化的,处于稳定态的原子的电子,绕核作圆周运动,但不辐射能量。 ②轨道是量子化的,其量矩 n h L = n = 2 ;n=1,2……;n 为量子数 ③电子跃迁时,发射或吸收能量为: h = En − Ek 2 H 原子轨道半径和能量的计算: 根据牛顿定律有: 2 2 0 2 4 v m e = (1) 又由假设(2): L = mv = n (2) 由(1)、(2)两式解得: 2 2 2 2 0 2 2 4 0 n me h n me n = = (3) n=1,2,3…… 原子核 核外电子