《电路》课程教学资源（课后课件）有例题_第15章 -1电路方程的矩阵形式

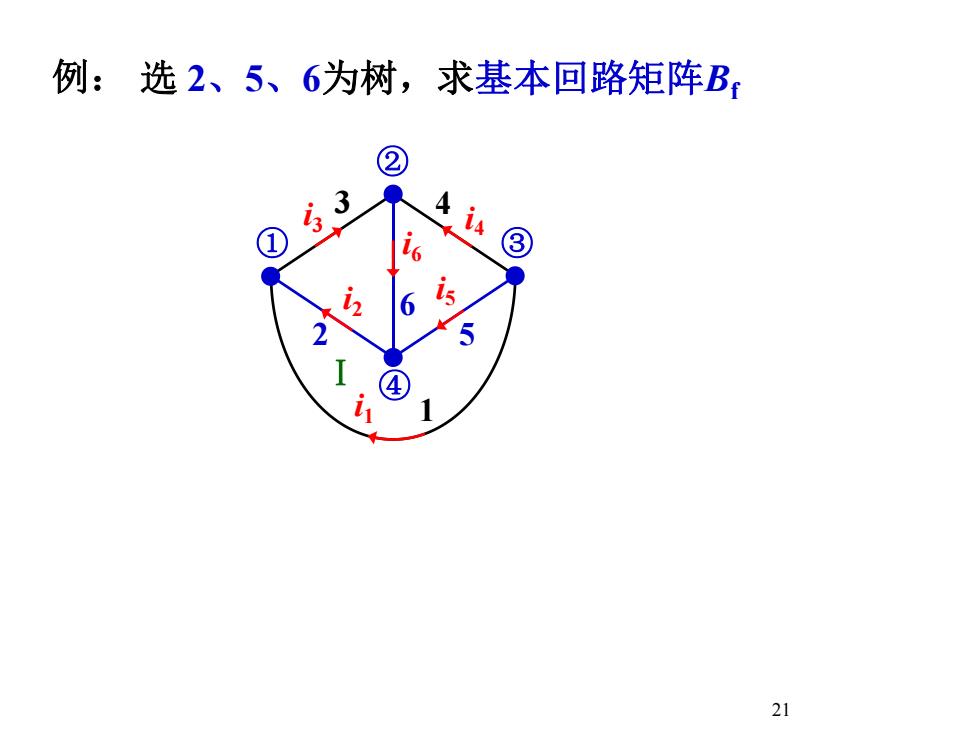
例：选2、5、6为树，求基本回路矩阵B,③isi652I4121

21 例： Ⅰ 1 3 i3 4 i4 i6 6 ① ② ③ ④i1 2 i2 5 i5 选 2、5、6为树，求基本回路矩阵Bf

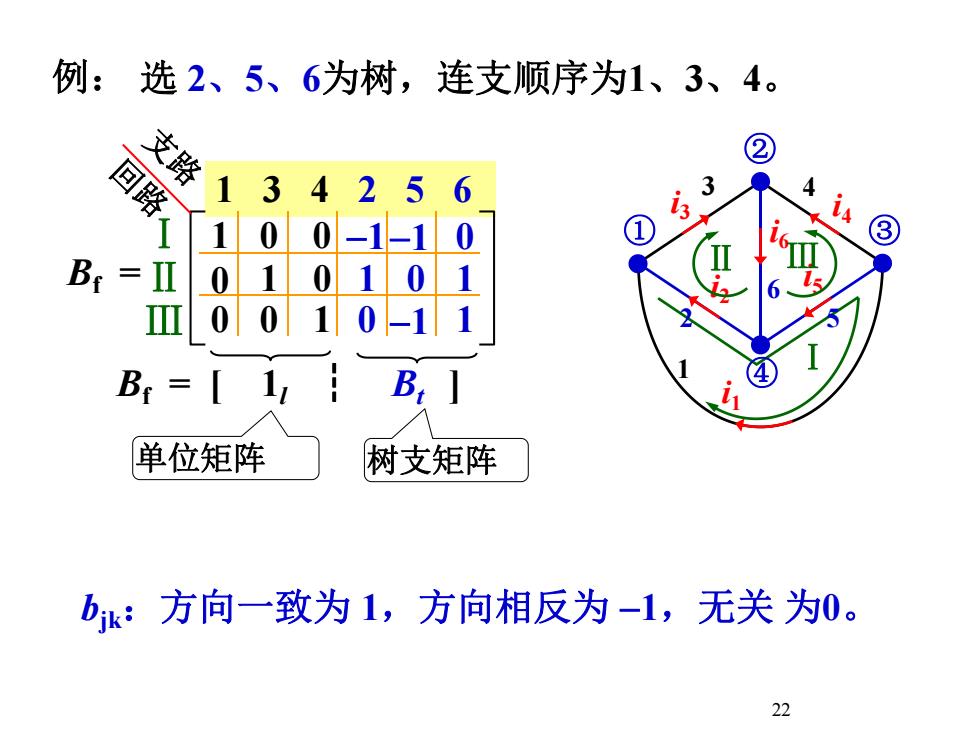
例：选2、5、6为树，连支顺序为1、3、4。支路2回路341210013B.010力010010III-111,B,B1单位矩阵树支矩阵bik：方向一致为1，方向相反为-1，无关为0。22

22 Bf = [ 1l ┆ Bt ] 例： 1 0 0 -1-1 0 0 1 0 1 0 1 0 0 1 0 -1 1 Ⅰ Ⅱ Ⅲ 1 3 4 2 5 6 Bf = 回路 支路 bjk：方向一致为 1，方向相反为 -1，无关 为0。 选 2、5、6为树，连支顺序为1、3、4。 单位矩阵 树支矩阵 1 Ⅰ 3 i3 4 i4 i6 6 ① ② ③ ④i1 2 i2 5 i5 Ⅱ Ⅲ

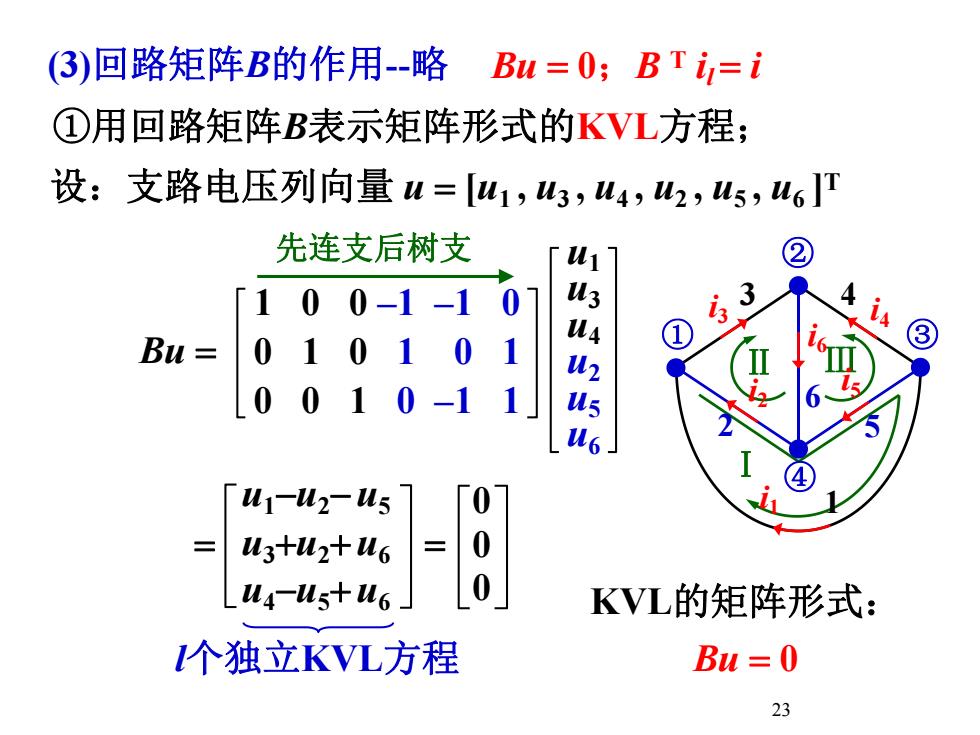
(3)回路矩阵B的作用--略Bu= O; B Ti=i①用回路矩阵B表示矩阵形式的KVL方程;设：支路电压列向量u=[ui，，4，2，us，u]I先连支后树支2ui3us41001-13u4130Bu =011TIIu2i20010usIu640ui-u2-us0=u3+u2+u60u4-us+u6KVL的矩阵形式：1个独立KVL方程Bu = 023

23 (3)回路矩阵B的作用-略 1 0 0 –1 –1 0 0 1 0 1 0 1 0 0 1 0 –1 1 u1 u3 u4 u2 u5 u6  0 0 0 Bu  设：支路电压列向量 u  [u1 , u3 , u4 , u2 , u5 , u6 ]T Ⅰ Ⅱ Ⅲ 1 3 i3 4 i4 i6 6 ① ② ③ ④i1 2 i2 5 i5 KVL的矩阵形式： Bu  0 u1-u2- u5 u3u2 u6 u4-u5 u6  l个独立KVL方程 先连支后树支 Bu  0；B T il  i ①用回路矩阵B表示矩阵形式的KVL方程；

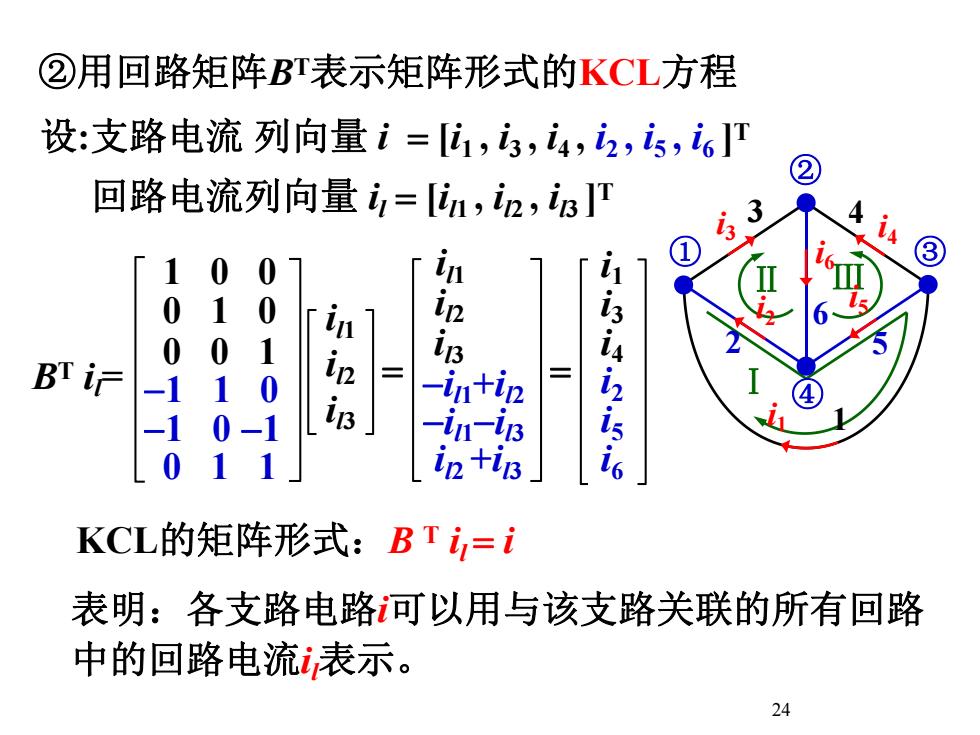
②用回路矩阵BT表示矩阵形式的KCL方程设：支路电流列向量i=[i，i,i,]2回路电流列向量i=[iu,in,i]]3i33W00I1in·3L500i56in:i4.i2.i5:ii.0inBT i记-in+in0-114in3-in-i30-1-1in +ir301KCL的矩阵形式：BTi=i表明：各支路电路河以用与该支路关联的所有回路中的回路电流表示。24

24 i1 i3 i4 i2 i5 i6  il1 il2 il3 -il1-il3 il2 +il3 il1 il2 il3 -il1+il2  Ⅰ Ⅱ Ⅲ 1 3 i3 4 i4 i6 6 ① ② ③ ④i1 2 i2 5 i5 设:支路电流 列向量 i  [i1 , i3 , i4 , i2 , i5 , i6 ]T 1 0 0 0 1 0 0 0 1 -1 0 -1 0 1 1 -1 1 0 回路电流列向量 il  [il1 , il2 , il3 ]T KCL的矩阵形式：B T il  i BT il= 表明：各支路电路i可以用与该支路关联的所有回路 中的回路电流il表示。 ②用回路矩阵BT表示矩阵形式的KCL方程

815-4 回路电流方程的矩阵形式1.典型复合支路特点2.支路方程的矩阵形式3.回路电流方程的矩阵形式4.较复杂电路分析(1)含受控电压源(2)含互感

§15-4 回路电流方程的矩阵形式 1.典型复合支路特点 2.支路方程的矩阵形式 3.回路电流方程的矩阵形式 4.较复杂电路分析 (1)含受控电压源 (2)含互感