
(一)函数在一点处可导的概念 1.1例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
(一) 函数在一点处可导的概念 1.引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系

(一)函数在一点处可导的概念 1.3引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
(一) 函数在一点处可导的概念 1.引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
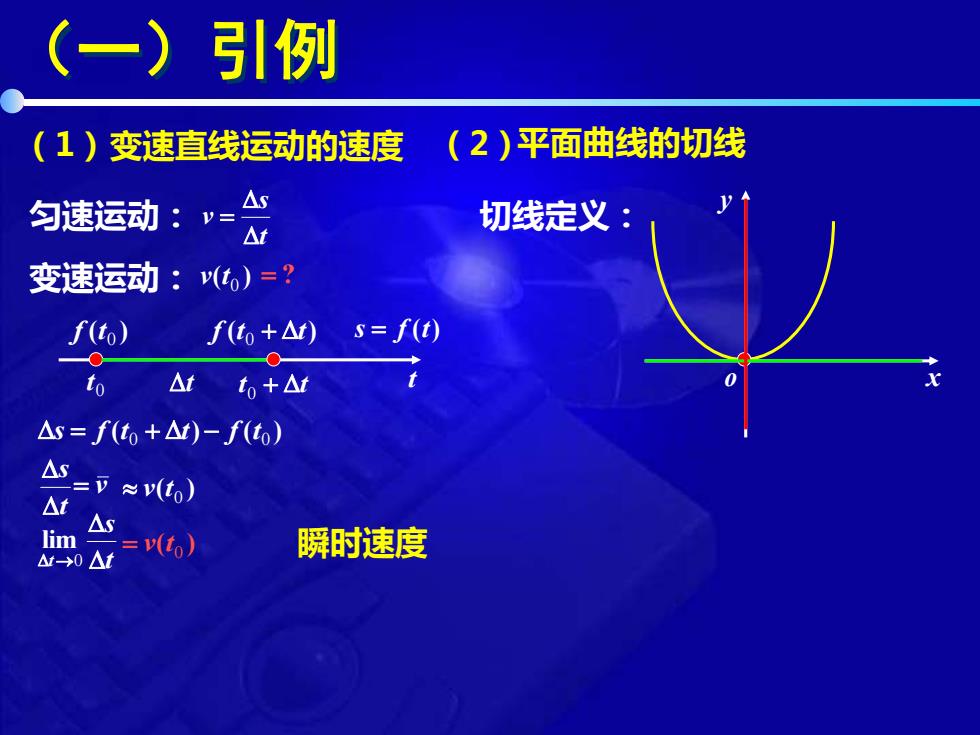
(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △t 变速运动:()=? f(tò) f(t+△) s=f(t) 0 to △t to+△r △s=f(t+△r)-f(to) =v≈(to) t △S lim △→0△t =t6) 瞬时速度
x y o (一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义:

(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △ 变速运动:v()=? f(to) f(to+△) s=f(t) M to △r to+△r 0 △s=f(i+△)-f(o) =v≈v(t) At △S lim M-0△t =v(t) 瞬时速度
(一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义: x y o M N

(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △t 变速运动:()=? f(tò) f(t,+△) s=f(t) M 0 to △t to+△r △s=f(t+△r)-f(to) =v≈(to) t △s lim →0△t =t6) 瞬时速度
(一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义: x y o M N