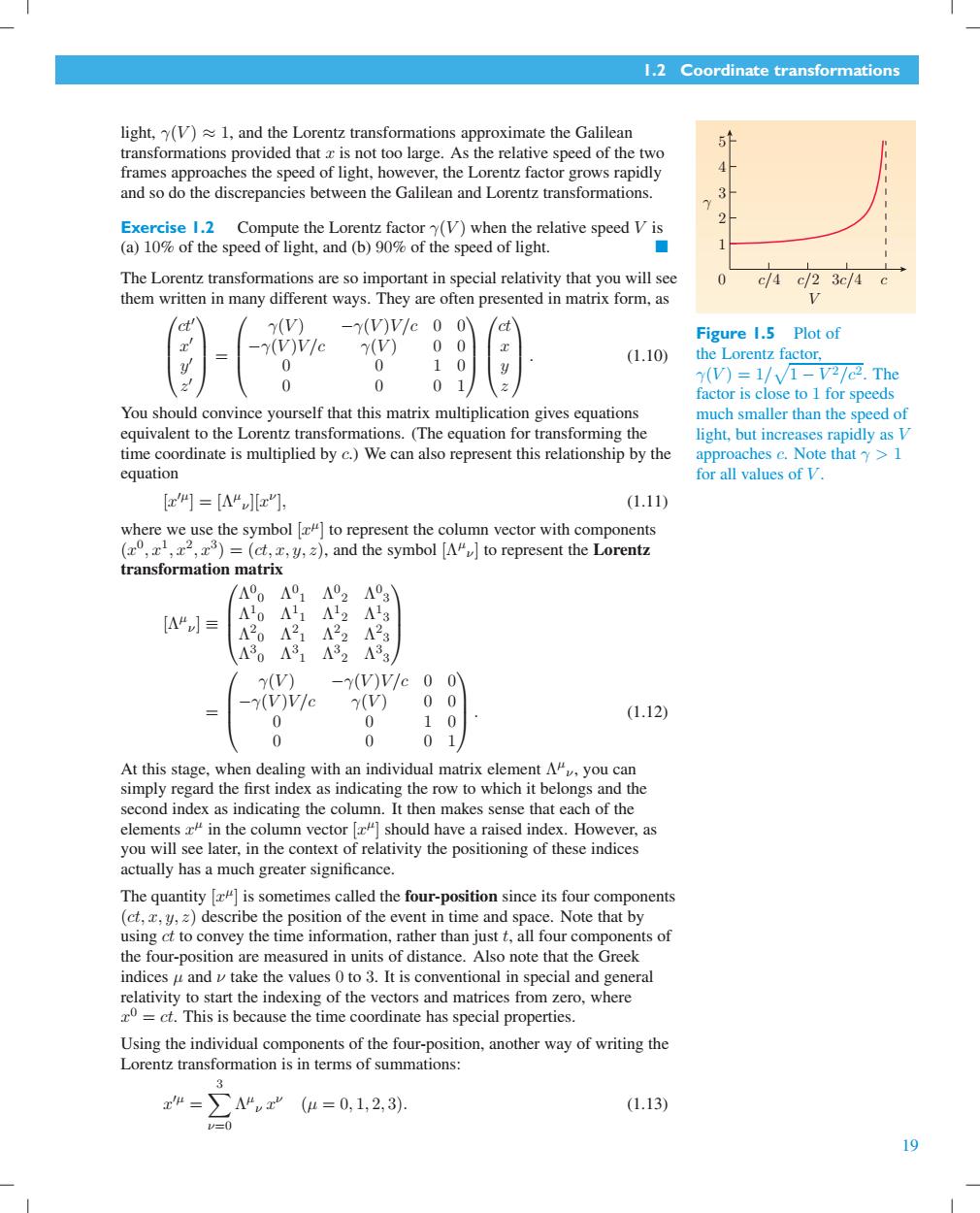
1.2 Coordinate transformations light,(V)1,and the Lorentz transformations approximate the Galilean 51 transformations provided that z is not too large.As the relative speed of the two frames approaches the speed of light,however,the Lorentz factor grows rapidly 4 and so do the discrepancies between the Galilean and Lorentz transformations. 2 3 2 Exercise 1.2 Compute the Lorentz factor y(V)when the relative speed V is (a)10%of the speed of light,and (b)90%of the speed of light. ■ The Lorentz transformations are so important in special relativity that you will see 0 c/4c/23c/4c them written in many different ways.They are often presented in matrix form,as ct' Y(V) -(V)V/e0 0 d Figure 1.5 Plot of (V)V/c (V) 0 0 0 0 0 (1.10) the Lorentz factor, y 0 0 0 Y(V)=1/V1-V2/2.The 2 factor is close to 1 for speeds You should convince yourself that this matrix multiplication gives equations much smaller than the speed of equivalent to the Lorentz transformations.(The equation for transforming the light,but increases rapidly as V time coordinate is multiplied by c.)We can also represent this relationship by the approaches c.Note that >1 equation for all values of V. [z4]=A“a"], (1.11) where we use the symbol [to represent the column vector with components (z0,1,2,3)=(ct,,y,z),and the symbol [AM]to represent the Lorentz transformation matrix A00A01 A02 A03 [A“≡ Λ12Λ13 A201 21A22 423 430A31A32433 Y(V) -(V)V/c 0 0 -y(V)V/c 7(V) 0 0 0 0 10 (1.12) 0 0 0 1 At this stage,when dealing with an individual matrix element Av,you can simply regard the first index as indicating the row to which it belongs and the second index as indicating the column.It then makes sense that each of the elements x#in the column vector [x]should have a raised index.However,as you will see later,in the context of relativity the positioning of these indices actually has a much greater significance. The quantity [#]is sometimes called the four-position since its four components (ct,,y,z)describe the position of the event in time and space.Note that by using ct to convey the time information,rather than just t,all four components of the four-position are measured in units of distance.Also note that the Greek indices u and v take the values 0 to 3.It is conventional in special and general relativity to start the indexing of the vectors and matrices from zero,where 0=ct.This is because the time coordinate has special properties. Using the individual components of the four-position,another way of writing the Lorentz transformation is in terms of summations: 3 x4=>△“x'(4=0,1,2,3) (1.13) =0 19
1.2 Coordinate transformations light, γ(V ) ≈ 1, and the Lorentz transformations approximate the Galilean transformations provided that x is not too large. As the relative speed of the two frames approaches the speed of light, however, the Lorentz factor grows rapidly and so do the discrepancies between the Galilean and Lorentz transformations. γ 0 1 2 4 3 5 c/4 c/2 3c/4 c V Figure 1.5 Plot of the Lorentz factor, γ(V ) = 1/ - 1 − V 2/c2. The factor is close to 1 for speeds much smaller than the speed of light, but increases rapidly as V approaches c. Note that γ > 1 for all values of V . Exercise 1.2 Compute the Lorentz factor γ(V ) when the relative speed V is (a) 10% of the speed of light, and (b) 90% of the speed of light. ■ The Lorentz transformations are so important in special relativity that you will see them written in many different ways. They are often presented in matrix form, as ct% x % y % z % = γ(V ) −γ(V )V /c 0 0 −γ(V )V /c γ(V ) 0 0 0 0 1 0 0 0 0 1 ct x y z . (1.10) You should convince yourself that this matrix multiplication gives equations equivalent to the Lorentz transformations. (The equation for transforming the time coordinate is multiplied by c.) We can also represent this relationship by the equation [x %µ ] = [Λµ ν][x ν ], (1.11) where we use the symbol [x µ ] to represent the column vector with components (x 0 , x1 , x2 , x3 ) = (ct, x, y, z), and the symbol [Λµ ν ] to represent the Lorentz transformation matrix [Λµ ν ] ≡ Λ 0 0 Λ 0 1 Λ 0 2 Λ 0 3 Λ 1 0 Λ 1 1 Λ 1 2 Λ 1 3 Λ 2 0 Λ 2 1 Λ 2 2 Λ 2 3 Λ 3 0 Λ 3 1 Λ 3 2 Λ 3 3 = γ(V ) −γ(V )V /c 0 0 −γ(V )V /c γ(V ) 0 0 0 0 1 0 0 0 0 1 . (1.12) At this stage, when dealing with an individual matrix element Λ µ ν , you can simply regard the first index as indicating the row to which it belongs and the second index as indicating the column. It then makes sense that each of the elements x µ in the column vector [x µ ] should havearaised index. However, as you will see later, in the context of relativity the positioning of these indices actually has a much greater significance. The quantity [x µ ] is sometimes called the four-position since its four components (ct, x, y, z) describe the position of the event in time and space. Note that by using ct to convey the time information, rather than just t, all four components of the four-position are measured in units of distance. Also note that the Greek indices µ and ν take the values 0 to 3. It is conventional in special and general relativity to start the indexing of the vectors and matrices from zero, where x 0 = ct. This is because the time coordinate has special properties. Using the individual components of the four-position, another way of writing the Lorentz transformation is in terms of summations: x %µ = A 3 ν=0 Λ µ ν x ν (µ = 0, 1, 2, 3). (1.13) 19

Chapter I Special relativity and spacetime This one line really represents four different equations,one for each value of u. When an index is used in this way,it is said to be a free index,since we are free to give it any value between 0 and 3,and whatever choice we make indicates a different equation.The index v that appears in the summation is not free,since whatever value we choose for u,we are required to sum over all possible values of v to obtain the final equation.This means that we could replace all appearances of v by some other index,a say,without actually changing anything.An index that is summed over in this way is said to be a dummy index. Familiarity with the summation form of the Lorentz transformations is particularly useful when beginning the discussion of general relativity;you will meet many such sums.Before moving on,you should convince yourself that you can easily switch between the use of separate equations,matrices (including the use of four-positions)and summations when representing Lorentz transformations. Given the coordinates of an event in frame S,the Lorentz transformations tell us the coordinates of that same event as observed in frame S'.It is equally important that there is some way to transform coordinates of an event in frame S'back into the coordinates in frame S.The transformations that perform this task are known as the inverse Lorentz transformations. The inverse Lorentz transformations t=y(V)(t+Vz'/c2). (1.14) x=Y(V)(z'+Vt'), (1.15) y=y, (1.16) 2=d. (1.17) Note that the only difference between the Lorentz transformations and their inverses is that all the primed and unprimed quantities have been interchanged,and the relative speed of the two frames,V,has been replaced by the quantity-V.(This changes the transformations but not the value of the Lorentz factor,which depends only on V2,so can still be written as y(V).)This relationship between the transformations is expected,since frame S'is moving with speed V in the positive r-direction as measured in frame S,while frame S is moving with speed V in the negative a'-direction as measured in frame S'. You should confirm that performing a Lorentz transformation and its inverse transformation in succession really does lead back to the original coordinates,i.e. (ct,c,,2)→(ct,x,,)→(ct,x,y,z) An event occurs at coordinates (ct =3m,x=4m,y=0,z=0)in frame S according to an observer O.What are the coordinates of the same event in frame S'according to an observer O',moving with speed V =3c/4 in the positive x-direction,as measured in S? First,the Lorentz factor (V)should be computed: y(3c/4)=1/V1-32/42=4/W7. 20
Chapter 1 Special relativity and spacetime This one line really represents four different equations, one for each value of µ. When an index is used in this way, it is said to be a free index, since we are free to give it any value between 0 and 3, and whatever choice we make indicates a different equation. The index ν that appears in the summation is not free, since whatever value we choose for µ, we are required to sum over all possible values of ν to obtain the final equation. This means that we could replace all appearances of ν by some other index, α say, without actually changing anything. An index that is summed over in this way is said to be a dummy index. Familiarity with the summation form of the Lorentz transformations is particularly useful when beginning the discussion of general relativity; you will meet many such sums. Before moving on, you should convince yourself that you can easily switch between the use of separate equations, matrices (including the use of four-positions) and summations when representing Lorentz transformations. Given the coordinates of an event in frame S, the Lorentz transformations tell us the coordinates of that same event as observed in frame S % . It is equally important that there is some way to transform coordinates of an event in frame S % back into the coordinates in frame S. The transformations that perform this task are known as the inverse Lorentz transformations. The inverse Lorentz transformations t = γ(V )(t % + V x% /c2 ), (1.14) x = γ(V )(x % + V t% ), (1.15) y = y % , (1.16) z = z % . (1.17) Note that the only difference between the Lorentz transformations and their inverses is that all the primed and unprimed quantities have been interchanged, and the relative speed of the two frames, V , has been replaced by the quantity −V . (This changes the transformations but not the value of the Lorentz factor, which depends only on V 2 , so can still be written as γ(V ).) This relationship between the transformations is expected, since frame S % is moving with speed V in the positive x-direction as measured in frame S, while frame S is moving with speed V in the negative x % -direction as measured in frame S % . You should confirm that performing a Lorentz transformation and its inverse transformation in succession really does lead back to the original coordinates, i.e. (ct, x, y, z) → (ct% , x% , y% , z% ) → (ct, x, y, z). ● An event occurs at coordinates (ct = 3 m, x = 4 m, y = 0, z = 0) in frame S according to an observer O. What are the coordinates of the same event in frame S % according to an observer O% , moving with speed V = 3c/4 in the positive x-direction, as measured in S? ❍ First, the Lorentz factor γ(V ) should be computed: γ(3c/4) = 1/ - 1 − 3 2/4 2 = 4/ √ 7. 20

.2 Coordinate transformations The new coordinates are then given by the Lorentz transformations: ct'=cy(3c/4)t-3x/4c)=(4/W7)(3m-3c×4m/4c)=0m, x'=y(3c/4)(x-3tc/4)=(4/W7)(4m-3×3m/4)=V7m ==0m, =z=0m. ct Exercise 1.3 The matrix equation x= x(V) -(V)V/c ct Y(V)V/e Y() (x no acceleration can be inverted to determine the coordinates(ct,)in terms of(ct',)Show that inverting the 2 x 2 matrix leads to the inverse Lorentz transformations in Equations 1.14 and 1.15. ■ 1.2.3 A derivation of the Lorentz transformations ct This subsection presents a derivation of the Lorentz transformations that relates the coordinates of an event in two inertial frames,S and S',that are in standard configuration.It mainly ignores the y-and z-coordinates and just considers the particle observed transformation of the t-and x-coordinates of an event.A general transformation to accelerate if relating the coordinates (t',x')of an event in frame S'to the coordinates (t,x)of higher-order terms the same event in frame S may be written as are left in t=ao+at+azz+a3t2+ax2+.., (1.18) 0 =bo+b1x+b2t+b322+b4t2+.. (1.19) Figure 1.6 Leaving where the dots represent additional terms involving higher powers of x or t. higher-order terms in the Now,we know from the definition of standard configuration that the event coordinate transformations marking the coincidence of the origins of frames S and S'has the coordinates would cause uniform motion in (t,)=(0,0)in S and (t',')=(0,0)in S'.It follows from Equations 1.18 one inertial frame S to be and 1.19 that the constants ao and bo are zero. observed as accelerated motion The transformations in Equations 1.18 and 1.19 can be further simplified by the in the other inertial frame S'. requirement that the observers are using inertial frames of reference.Since These diagrams,in which the Newton's first law must hold in all inertial frames of reference,it is necessary that vertical axis represents time an object not accelerating in one set of coordinates is also not accelerating in the multiplied by the speed of light other set of coordinates.If the higher-order terms in x and t were not zero,then an show that if the t2 terms were object observed to have no acceleration in S(such as a spaceship with its thrusters left in the transformations.then off moving on the line c=vt,shown in the upper part of Figure 1.6)would be motion with no acceleration in observed to accelerate in terms of x'and t'(i.e.''t,as indicated in the lower frame S would be transformed part of Figure 1.6).Observer O would report no force on the spaceship,while into motion with non-zero observer O'would report some unknown force acting on it.In this way,the two acceleration in frame S'.This observers would register different laws of physics,violating the first postulate of would imply change in velocity special relativity.The higher-order terms are therefore inconsistent with the without force in S',in conflict required physics and must be removed,leaving only a linear transformation. with Newton's first law. So we expect the special relativistic coordinate transformation between two frames in standard configuration to be represented by linear equations of the form t'=at a2x, (1.20) x'=bix+b2t. (1.21) 21
1.2 Coordinate transformations The new coordinates are then given by the Lorentz transformations: ct% = cγ(3c/4)(t − 3x/4c) = (4/ √ 7)(3 m − 3c × 4 m/4c) = 0 m, x % = γ(3c/4)(x − 3tc/4) = (4/ √ 7)(4 m − 3 × 3 m/4) = √ 7 m, y % = y = 0 m, z % = z = 0 m. Exercise 1.3 The matrix equation ? ct% x % @ = ? γ(V ) −γ(V )V /c −γ(V )V /c γ(V ) @ ?ct x @ can be inverted to determine the coordinates (ct, x) in terms of (ct% , x% ). Show that inverting the 2 × 2 matrix leads to the inverse Lorentz transformations in Equations 1.14 and 1.15. ■ 1.2.3 A derivation of the Lorentz transformations This subsection presents a derivation of the Lorentz transformations that relates the coordinates of an event in two inertial frames, S and S % , that are in standard configuration. It mainly ignores the y- and z-coordinates and just considers the transformation of the t- and x-coordinates of an event. A general transformation relating the coordinates (t % , x% ) of an event in frame S % to the coordinates (t, x) of the same event in frame S may be written as t % = a0 + a1t + a2x + a3t 2 + a4x 2 + ··· , (1.18) x % = b0 + b1x + b2t + b3x 2 + b4t 2 + ··· , (1.19) where the dots represent additional terms involving higher powers of x or t. Now, we know from the definition of standard configuration that the event marking the coincidence of the origins of frames S and S% has the coordinates (t, x) = (0, 0) in S and (t % , x% )=(0, 0) in S % . It follows from Equations 1.18 and 1.19 that the constants a0 and b0 are zero. ct S S " x " ct" no acceleration x particle observed to accelerate if higher-order terms are left in O O" Figure 1.6 Leaving higher-order terms in the coordinate transformations would cause uniform motion in one inertial frame S to be observed as accelerated motion in the other inertial frame S % . These diagrams, in which the vertical axis represents time multiplied by the speed of light, show that if the t 2 terms were left in the transformations, then motion with no acceleration in frame S would be transformed into motion with non-zero acceleration in frame S % . This would imply change in velocity without force in S % , in conflict with Newton’s first law. The transformations in Equations 1.18 and 1.19 can be further simplified by the requirement that the observers are using inertial frames of reference. Since Newton’s first law must hold in all inertial frames of reference, it is necessary that an object not accelerating in one set of coordinates is also not accelerating in the other set of coordinates. If the higher-order terms in x and t were not zero, then an object observed to have no acceleration in S (such as a spaceship with its thrusters off moving on the line x = vt, shown in the upper part of Figure 1.6) would be observed to accelerate in terms of x % and t % (i.e. x % =4 v % t % , as indicated in the lower part of Figure 1.6). Observer O would report no force on the spaceship, while observer O% would report some unknown force acting on it. In this way, the two observers would register different laws of physics, violating the first postulate of special relativity. The higher-order terms are therefore inconsistent with the required physics and must be removed, leaving only a linear transformation. So we expect the special relativistic coordinate transformation between two frames in standard configuration to be represented by linear equations of the form t % = a1t + a2x, (1.20) x % = b1x + b2t. (1.21) 21