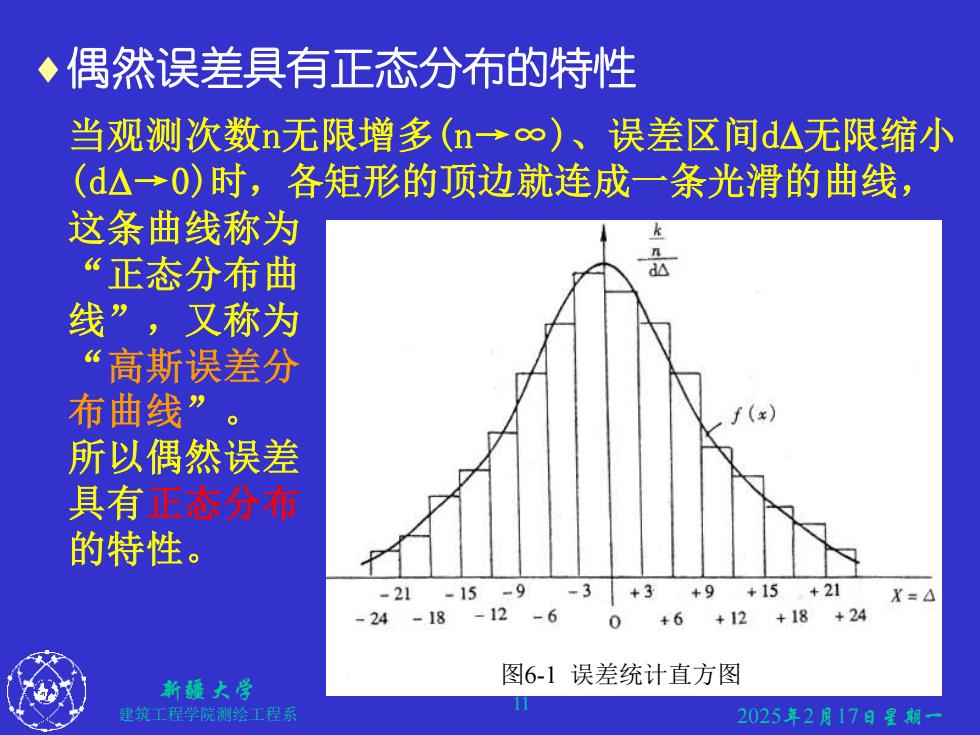
◆偶然误差具有正态分布的特性 当观测次数n无限增多(n→∞)、误差区间d△无限缩小 (d△→O)时,各矩形的顶边就连成一条光滑的曲线, 这条曲线称为 “正态分布曲 d△ 线”,又称为 “高斯误差分 布曲线”。 所以偶然误差 具有正态分布 的特性。 -21 -15 -9 -3 +3+9+15,+21 X=△ -24-18-12 -6 0+6+12+18+24 新疆大学 图6-1误差统计直方图 建筑工程学院测绘工程系 2025年2月17日星期
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 11 偶然误差具有正态分布的特性 当观测次数n无限增多(n→∞)、误差区间d无限缩小 (d→0)时,各矩形的顶边就连成一条光滑的曲线, 这条曲线称为 “正态分布曲 线”,又称为 “高斯误差分 布曲线” 。 所以偶然误差 具有正态分布 的特性。 图6-1 误差统计直方图

§6.4 衡量精度的指标 1.方差与标准差 ◆由正态分布密度函数 )=2 1 (x-a)2 -e 2.2 正态分布曲线(a-0 式中a、g为常数;e=2.72828. 令:△=x-a,上式为: X y=f(△)= √2πo 新疆大学 建筑工程学院测绘工程系 12 2025年2月17日星期一
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 12 1.方差与标准差 由正态分布密度函数 ( ) ( ) 2 2 2 2 1 x a x e − − = 式中 a 、 为常数; e =2.72828. x= y 正态分布曲线(a=0) 令: = x −a ,上式为: 2 2 2 2 1 ( ) − y = f = e §6.4 衡量精度的指标

◆标准差σ的数学意义 G较小 43 y=f)=2xa O较大 上式中,g称为方差: 表示△的 XF△ 离散程度 2 a"lim △公+△3+.+△ n→>0 n 1n-→o0 σ称为标准差: o=lim =±lim n→o 1-→0 n 新疆大学 建筑工程学院测绘工程系 13 2025年2月17日星期一
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 13 标准差 的数学意义 2 2 2 2 1 ( ) − y = f = e 表示的 离散程度 x= y 较小 较大 n n n n [ ] lim [ ] lim 2 = = → → 称为标准差: n n n n n [ ] lim lim 2 2 2 2 2 2 1 = + + + = → → 2 上式中, 称为方差:

·测量工作中,用中误差作为衡量观测值精度的标准。 中误差 观测次数无限多时,用标准差。表示偶然误差的离散情形: o=±lim n>0 n 观测次数n有限时,用中误差m表示偶然误差的离散情形: △△ m= n n 上式中,偶然误差△为观测值与真值X之差: △=l1-X 新疆大学 建筑工程学院测绘工程系 2025年2月17日星期一
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 14 测量工作中,用中误差作为衡量观测值精度的标准。 中误差: 观测次数无限多时,用标准差 表示偶然误差的离散情形: n n [ ] lim = → 上式中,偶然误差为观测值与真值X之差: 观测次数n有限时,用中误差m表示偶然误差的离散情形: n n m n [ ] 2 2 2 2 1 = + + + = i=i - X
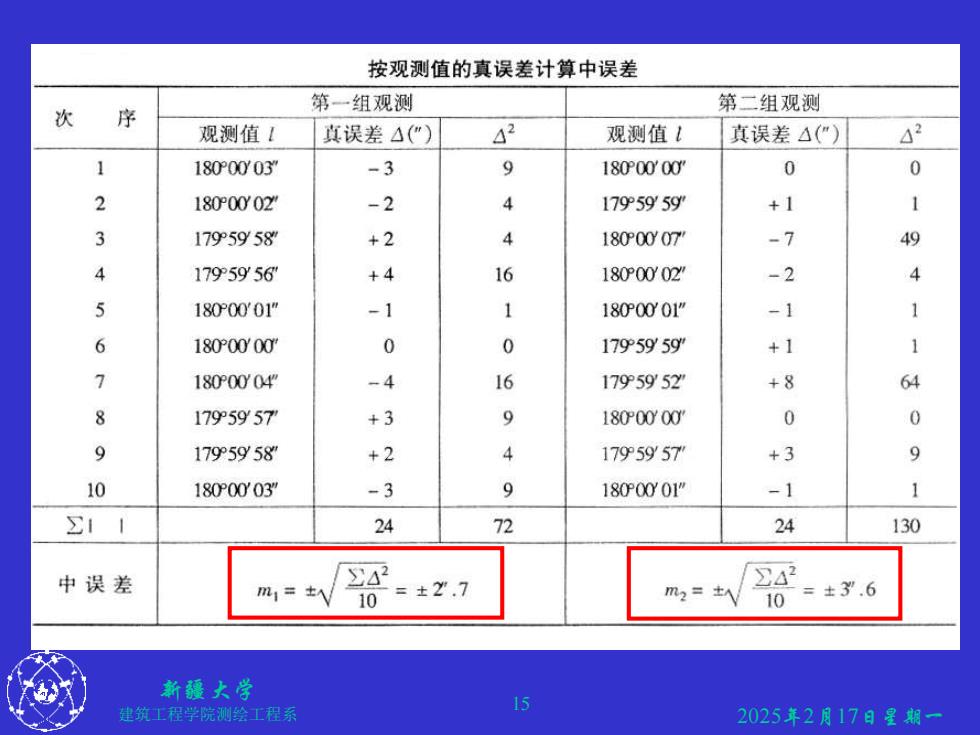
按观测值的真误差计算中误差 第一组观测 第二组观测 次 序 观测值1 真误差△() 42 观测值! 真误差△(") △2 1 1800003 -3 9 1800000Y 0 0 2 1800002Y -2 1795959y +1 1 3 1795958 +2 4 1800007 -7 49 1795956 +4 16 1800002Y -2 4 5 1800001" -1 1 180G0001" -1 1 6 1800000 0 0 1795959y +1 1 7 180P0004 -4 16 1795952 +8 64 8 1795957 +3 9 1800W0W 0 9 1795958 +2 4 1795957 +3 9 10 180P0003 -3 9 1800001" -1 1 ∑11 24 72 24 130 中误差 42 m= 10 =±Y.7 ∑△2 m2= 10 =±3Y.6 新疆大学 建筑工程学院测绘工程系 15 2025年2月17日星期一
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 15 P123表5-2