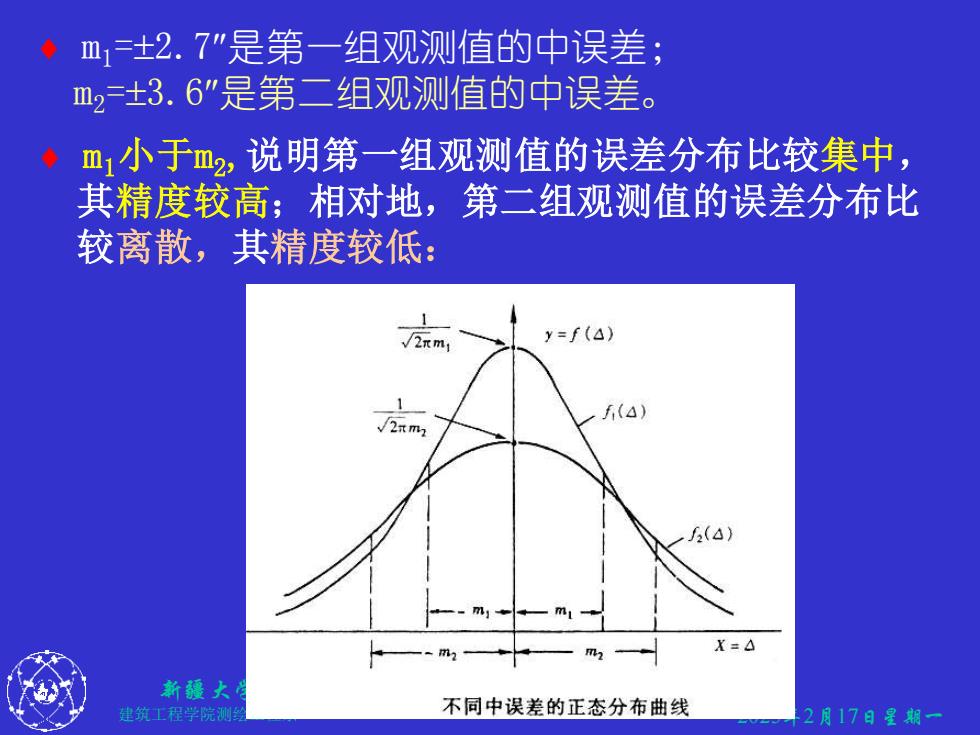
m±2.7"是第一组观测值的中误差; m2±3.6”是第二组观测值的中误差。 ◆ m1小于m2,说明第一组观测值的误差分布比较集中, 其精度较高;相对地,第二组观测值的误差分布比 较离散,其精度较低: √2πm1 y=f(A) f(4) √/2m m X=△ 新疆大 建筑工程学院测 不同中误差的正态分布曲线 2月17日星期一
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 16 m1小于m2,说明第一组观测值的误差分布比较集中, 其精度较高;相对地,第二组观测值的误差分布比 较离散,其精度较低: m1=2.7是第一组观测值的中误差; m2=3.6是第二组观测值的中误差

2.容许误差(极限误差 根据误差分布的密度函数, 误差出现在微分区间d△内的概 率为 △2 1 P(△)=f(△)d△= 2md△ √2元m 误差出现在K倍中误差区间内的概率为: ♪Ncan-2sn 2m d△ 将K=1、2、3分别代入上式,可得到偶然误差分别出现在 一倍、二倍、三倍中误差区间内的概率: P(4≤m)=0.683=68.3% P(△s2m)=0.954=95.4% P(△s3m=0.997=99.7% 测量中,一般取两倍中误差(2m)作为容许误差,也称为限差: 1△容=3醐ml或△容=2m 新疆大学 17 建筑工程学院测绘工程系 2025年2月17日星期
2025年2月17日星期一 新疆大学 建筑工程学院测绘工程系 17 2.容许误差(极限误差) 根据误差分布的密度函数,误差出现在微分区间d内的概 率为: = = − e d m P f d m 2 2 2 2 1 ( ) ( ) 误差出现在K倍中误差区间内的概率为: + − − = km km m e d m P k m 2 2 2 2 1 ( ) 将K=1、2、3分别代入上式,可得到偶然误差分别出现在 一倍、二倍、三倍中误差区间内的概率: P(|| m)=0.683=68.3 P(||2m)=0.954=95.4 P(||3m)=0.997=99.7 测量中,一般取两倍中误差(2m)作为容许误差,也称为限差: |容|=3|m| 或 |容|=2|m|