
那么,对LTI系统来说,式2.3就变为 十 [n=∑x[k]hn-k] 式2.6 k=-∞ 式2.6又称为卷积和,其右边的运算称为xn和hn 的卷积,用符号记作 y n=xn]hn] 这意味着,既然一个LT系统对任意输入的响应可 以用系统对单位脉冲的响应来表示,那么LTI系统 的单位脉冲响应就完全刻画了系统的特性。 6比较式2.6和式2.3,其区别就在于是否是LT1系统, 在时刻k加入的输入xk引起的响应x[h[n-k就是 h[n移位并经加权的结果
那么,对LTI系统来说,式2.3就变为 式2.6又称为卷积和,其右边的运算称为x[n]和h[n] 的卷积,用符号记作 y[n] = x[n] * h[n] 这意味着,既然一个LTI系统对任意输入的响应可 以用系统对单位脉冲的响应来表示,那么LTI系统 的单位脉冲响应就完全刻画了系统的特性。 比较式2.6和式2.3,其区别就在于是否是LTI系统, 在时刻k加入的输入x [k]引起的响应x[k]h[n-k]就是 h [n]移位并经加权的结果。 [] [ ][ ] k yn xkhn k +∞ =−∞ = − 式2.6

卷积和 卷积和 y[n]=∑[k]hM[n-k] k=-∞ 或者 yn]=x n]h n] LTI系统的单位脉冲响应完全刻画了系统的特性 第2章线性时不变系统 17
第2章 线性时不变系统 17 卷积和 卷积和 +∞ =−∞ = − k knhkxny ][][][ 或者 y[n] = x[n] * h[n] LTI系统的单位脉冲响应完全刻画了系统的特性
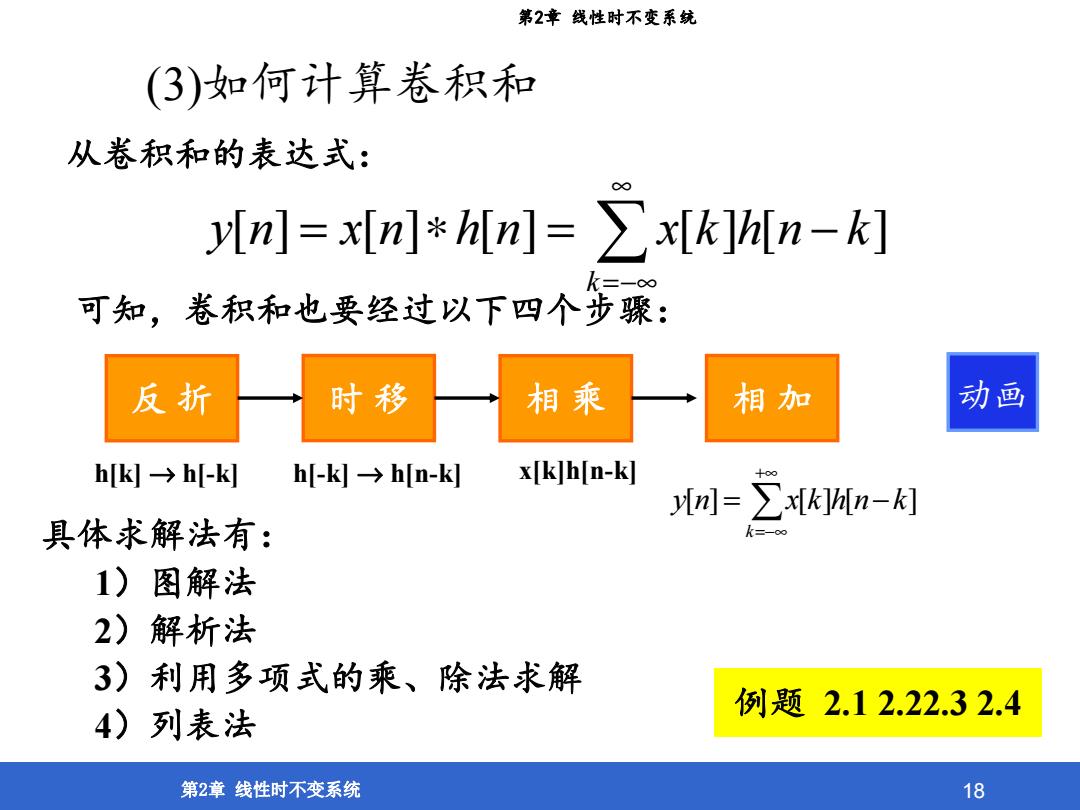
第2章线性时不变系统 (3)如何计算卷积和 从卷积和的表达式: ●● yIn]=x[n]hin]=x[kThin-k] 可知,卷积和也要经过以下四个步骤: 反折 时移 相乘 相加 动画 hk→h-k h-k→hn-k x[k]h[n-k] yn=∑xk[n-] 具体求解法有: 1)图解法 2)解析法 3)利用多项式的乘、除法求解 例题2.12.22.32.4 4)列表法 第2章线性时不变系统 18
第2章 线性时不变系统 18 (3)如何计算卷积和 从卷积和的表达式: ∞ =−∞ =∗= − k knhkxnhnxny ][][][][][ 可知,卷积和也要经过以下四个步骤: 反 折 时 移 相 乘 相 加 h[k] → h[-k] h[-k] → h[n-k] x[k]h[n-k] +∞ =−∞ = − k knhkxny ][][][ 例题 2.1 2.22.3 2.4 具体求解法有: 1)图解法 2)解析法 3)利用多项式的乘、除法求解 4)列表法 动画 第2章 线性时不变系统

第2章线性时不变系统 1)图解法 已知N和a,桌:y[n]=xn]小·hn] x[n] h(n] 12 0 012 第2章线性时不变系统 19
第2章 线性时不变系统 19 1)图解法 已知X[n]和h[n],求: 2 x[n] 1 n 0 1 1 2 0 1 2 h[n] 1 n 1 [] [] [] ⋅= nhnxny 第2章 线性时不变系统
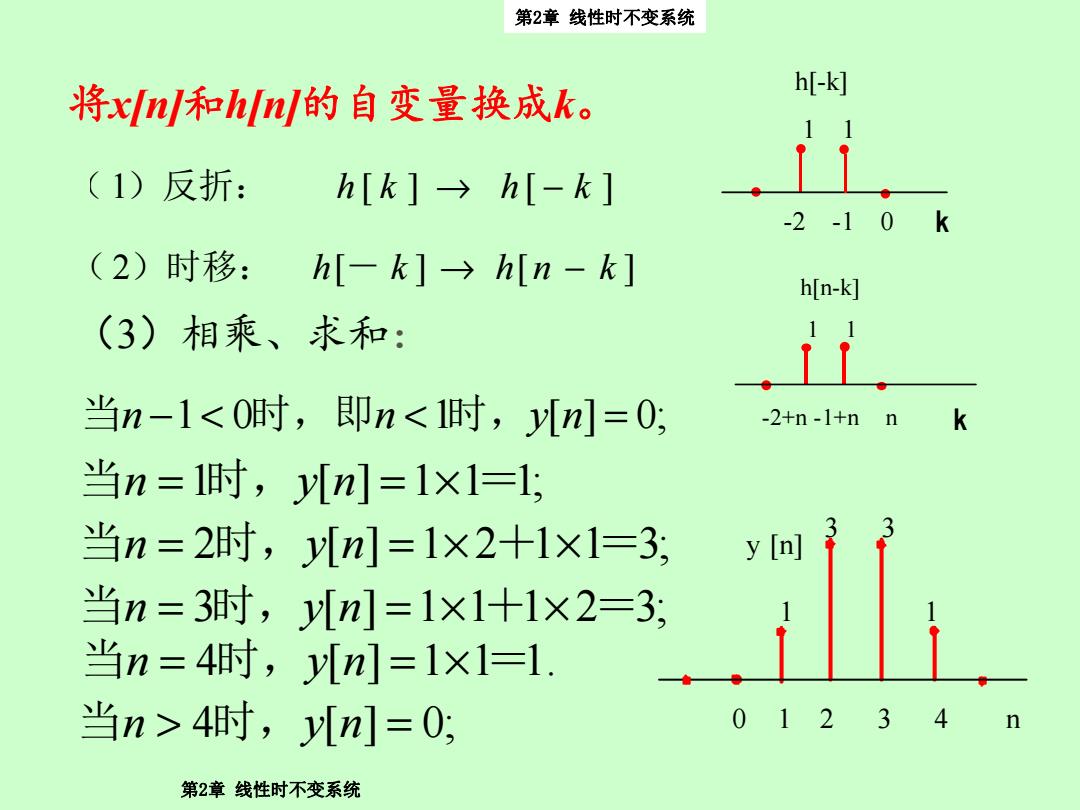
第2章线性时不变系统 h[-k] 将xn/和hln的自变量换成k。 (1)反折: h[k]→h[-k] 2 -10k (2)时移:h[-k]→h[n-k] h(n-k] (3)相乘、求和: 1 当n-1<0时,即n<1时,yn]=0; -2+n-1+nn k 当n=1时,yn=1×l=l; 当n=2时,y[n]=1×2+1×1=3, y[] 当n=3时,y[n]=1×1+1×2=3; 当n=4时,y[n]=1×1=1. 当n>4时,y[n]=0; 012 34 第2章线性时不变系统
第2章 线性时不变系统 ( 1)反折: −→ khkh ][][ (2)时移: - −→ knhkh ][][ -2 -1 0 n h[-k] 1 1 k -2+n -1+n n n h[n-k] 1 1 当n <− 01 时,即 < 时, nyn = ;0][1 k 0 1 2 3 4 n 3 3 1 1 y [n] (3)相乘、求和: 当 = 时, nyn ×= = ;111][1 当 = 时, nyn ××= =+ ;31121][2 当 = 时, nyn ××= =+ ;32111][3 当 = 时, nyn ×= = .111][4 当 > 时, nyn = ;0][4 将x[n]和h[n]的自变量换成k。 第2章 线性时不变系统