
1.1.3接收光功率 设距光源很远的R处有一个小接收面A,R>>(A)2。 接收面上的光场(视为平面光场)强度为 I(t,R)=G, P.(t-ta) 4πR2 P):点光源的功率变化函数 1FR/C:光源到R处的传输时延 G:A所在方向的发射光增益 特例:若点光源发射光场的功率恒定为P,则在R 处光束之内的光强度为 I(t,R)= 4R2

接收面A,收到的光功率是R处光强度在A,面上的积分 P.(t)=cose I(t,R)dA 0:接收面A,的法线与光功率流传输方向间的夹角 讨论: 若0=O,则A,上所接收的光功率: P=( GP)A. 4πR2 [发射增益为G,的光源所产生的电磁场标准功率流方程] 接收增益,定义为: 4π、 G,=(京)A 则 P=PG,LG, ←一物理意义理解 ,=(?片波长A的电磁场在传输距离R后的树耗

1.2光接收机视场 ·光接收机内,输入光场一般都是由前端面上的光学元件收 集并汇聚到探测器表面(图1.2-1所示) 透镜变换特性影响到达探测器上的光场分布 透镜面积4少 物理本质:衍射场 焦点区 注: 适当设计接收机透 收集到透镜输 聚焦光场 镜,可以在焦平面 入瑞的光场 得到夫琅和费衍射 光阑平面(x)) 焦平面(u.) (接收机平面) (探测器平面) 图1.2-1光接收机的成像几何图形

1.2.1透镜变换 用ft,)表示在整个透镜光阑上接收到的光场, 用f(,u,v)表示焦平面上的衍射场,则: ∫(,,)= I(u,v) f.(t,x,y)exp[-j 2π (xu+yv)txdy(1.2-1) 元f. 元f (x,y)和(u,V)分别为光阑和焦平面上的场坐标,相因子 I(u.v)=exp[j-Z(u+v) (1.2-2) 元f f(t,u,v)还与∫(t,x,y)的二维傅里叶变换相联系,即若定义 F,(t,@.@2)=f(t,x,y)exp[-j(xo+y@2)dxdy (1.2-3) 为化,x,y)的二维空间傅里叶变换,则有
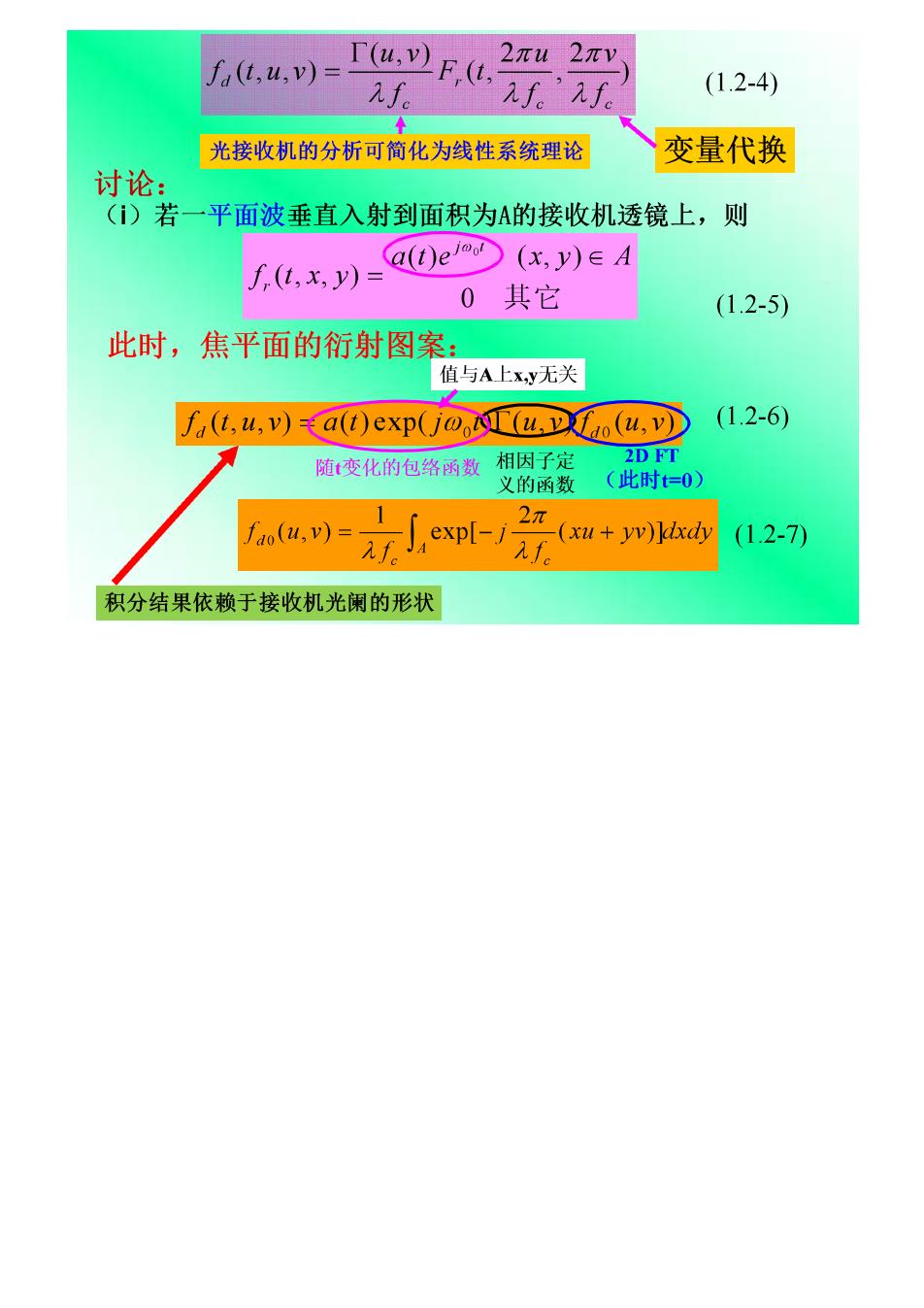
(t,u,v)= T(u.v)F(t. 2πu2πv (1.2-4) 光接收机的分析可简化为线性系统理论 变量代换 讨论: (1)若一平面波垂直入射到面积为A的接收机透镜上,则 a(t)e(x,y)EA f(t,x,y)= 0其它 (1.2-5) 此时,焦平面的衍射图 值与A上xy无关 f(t,u,v)a(t)exp(j(u.(u,v) (1.2-6) 随变化的包络函数相因子定 2D FT 义的函数 (此时t=0) ,2 f4o(4,)= -(x+yw)y(1.2-7) 积分结果依赖于接收机光阑的形状