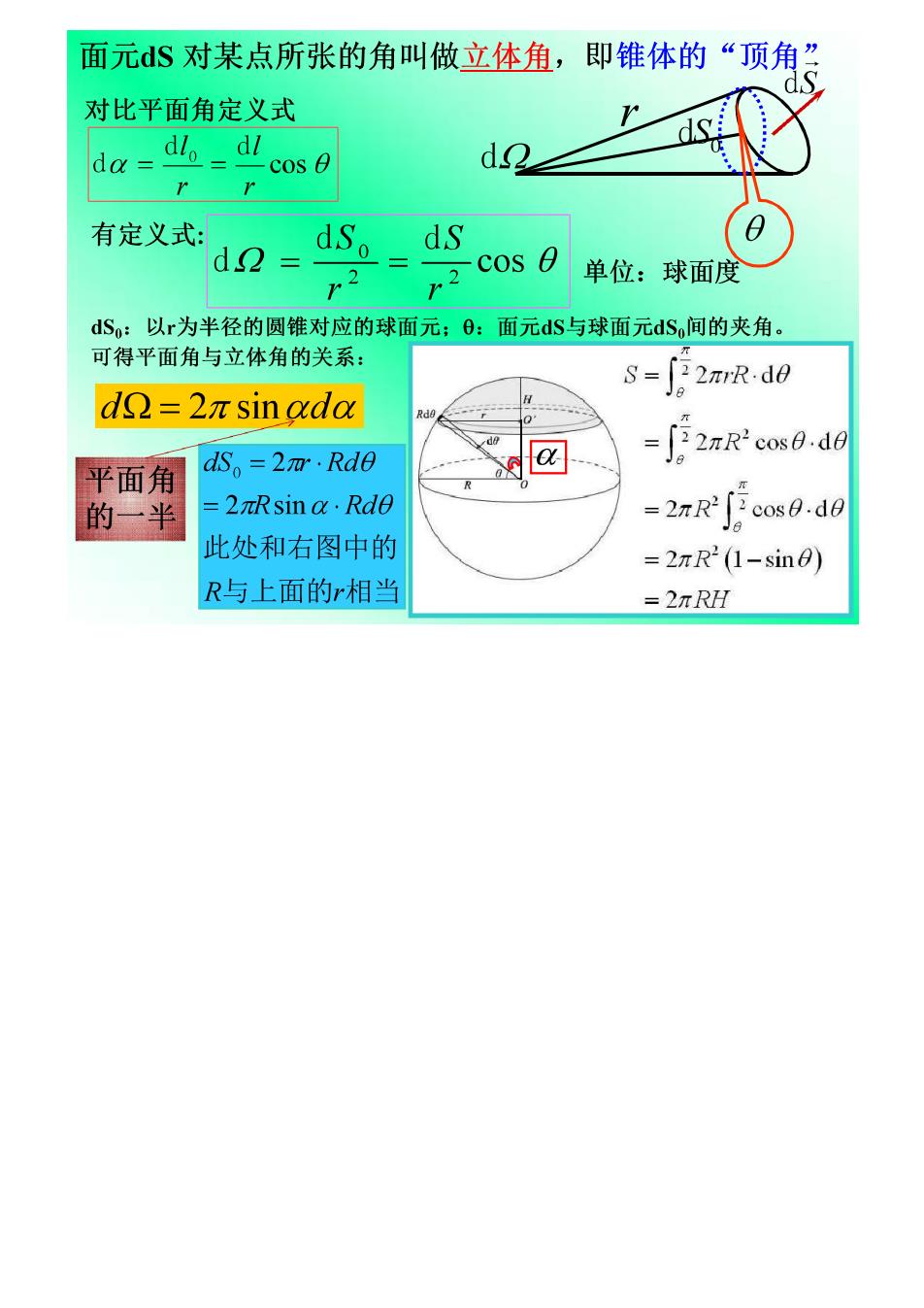
面元S对某点所张的角叫做立体角,即锥体的“顶角” 对比平面角定义式 da dlo=di -cos 0 有定义式: pd的 Cos8单位:球面度 dS:以r为半径的圆锥对应的球面元;0:面元dS与球面元dS,间的夹角。 可得平面角与立体角的关系: dn=2πsinada s-f2mR-d0 平面角 dS。=2m.Rd0 a☑ =J月2 nRcox0..dd 的一半 =2Rsin a.Rde -2nR[icos0.d0 此处和右图中的 =2rR2(1-sin0) R与上面的r相当 =2nRH

闭合平面曲线对曲线内一点所张的平面角 a-fdafgcas=54-2n 弧度 闭合曲面对面内一点所张的立体角 P=5an=f兴-续面度

1.1.2光源发射增益 (光接收机接收到的光功率与光发射机发射功率相关) 。光的辐射特性:光源的亮度函数L(0) 定义:给定的方向角0时,光源辐射的归一化功率。 单位:W/(srm)(瓦特每球面度平方米) >均匀辐射型光源(大部分光源) 辐射的总功率为:P,=LA、2 (A,:发光面积;Q。:辐射角) 光面积, 朗伯光源:Ω2.=2π(sr)P=2πLA > 辐射对称型光源 立体角2,与平面辐射角0,间的关系: 2、=2π[1-cos(0,/2)l 图1.1-5光反射角 2,=an=2πsinu0

·光束形成和光汇聚平面光束的直径 0+ :波长 4:输出透镜直径 :透镜的距离 注意:扩束准直后的光東在长距离空间通信中会扩展,而不是 平行光束,因为聚束透镜无法把光源场聚焦为一点 讨论: 光束形 成系统 >在近场时,z/d<1准直后 光束角 光束直径与透镜直径相同。 光源 >在远场时,1z/d>1光束直 透镜直径 径随距离的增加而扩大。扩 散的平面角约为 图1.1-6光束形成和光汇聚

衍射极限发送机光束角0。≈ -rad 对应的立体角: 透镜直径 0,=2al-cos0/21=平9 [注:cos6唯0=0附近的7ay1or展开式:cos0=分上旷0 台(2k 说明:长距离空间传输中,光波段与微波段相比, 优势是波长短、扩束角小几个量级(p5:例子) ·光汇聚的特征参量一有效天线增益 [概念移植:微波天线发射中,天线作用即汇聚电磁波,可移植到光波段] 4元4d G.= [试用条件:远场(上述二式决定)川 2 G越小越好,还是越大越好?