
由于斯皮尔曼一布朗公式有个基本假设,即:两个“半 测验”满足方差齐性,故 当数据资料不能满足这一 役设时,怎选下两朵等侨的公艺一: ①弗朗那根(Flanagan)公式 ri,=21-(s2+S:)/ 式中,S2和S2分别表示所有被试在两半测验上得分的 方差;S表示所有被试在整个测验上的总得分的方差。 ②卢仑(Rulon)公式 m=1-S/S2 式中,S表示同一组被试在两半测验上得分之差的方差
由于斯皮尔曼-布朗公式有个基本假设,即:两个“半 测验”满足方差齐性,故,当数据资料不能满足这一 假设时,应选择下述两个等价的公式之一: ①弗朗那根(Flanagan)公式 式中,Sa 2 和Sb 2分别表示所有被试在两半测验上得分的 方差;SX 2表示所有被试在整个测验上的总得分的方差。 ②卢仑(Rulon)公式 式中, Sd 2表示同一组被试在两半测验上得分之差的方差。 ( ) 2 2 2 t t 21 Sa Sb S X r = − + 2 2 tt 1 Sd S X r = −

补: ■方差与标准差 口1.基本概念 口一组数据中,各数离均差的平方和的算术平均数 称为这组数据的方差,文m均方差或变异数 ▣定义式: K,- S2= W 口方差的算术平方根称为标准差 口定义式: 2x,-x} S=V- i= N
补: ◼ 方差与标准差 1.基本概念 一组数据中,各数离均差的平方和的算术平均数 称为这组数据的方差,又叫均方差或变异数 定义式: 方差的算术平方根称为标准差 定义式: ( ) N X X S n i i = − = 1 2 2 ( ) N X X S n i i = − = 1 2

补: ■2.计算方差和标准差的简单方法
补: ◼ 2.计算方差和标准差的简单方法 2 2 2 = − N X N X S 2 2 = − N X N X S

估计同质性信度的方法: (2)克龙巴赫a系数 该方法适合对题目的题型较多的测验进行内部一致性信度分析。 估计测验信度采用克龙巴赫α系数,其计算公式为: 式中,为题目数,S,表示所有被试在第1道题上得分的 方差,S表示所有被试在整个测验上的总得分的方差
估计同质性信度的方法: (2) 克龙巴赫α系数 该方法适合对题目的题型较多的测验进行内部一致性信度分析。 估计测验信度采用克龙巴赫α系数,其计算公式为: 式中,K为题目数, Si 2表示所有被试在第i 道题上得分的 方差,SX 2表示所有被试在整个测验上的总得分的方差。 − − = 2 2 1 1 X i S S K K
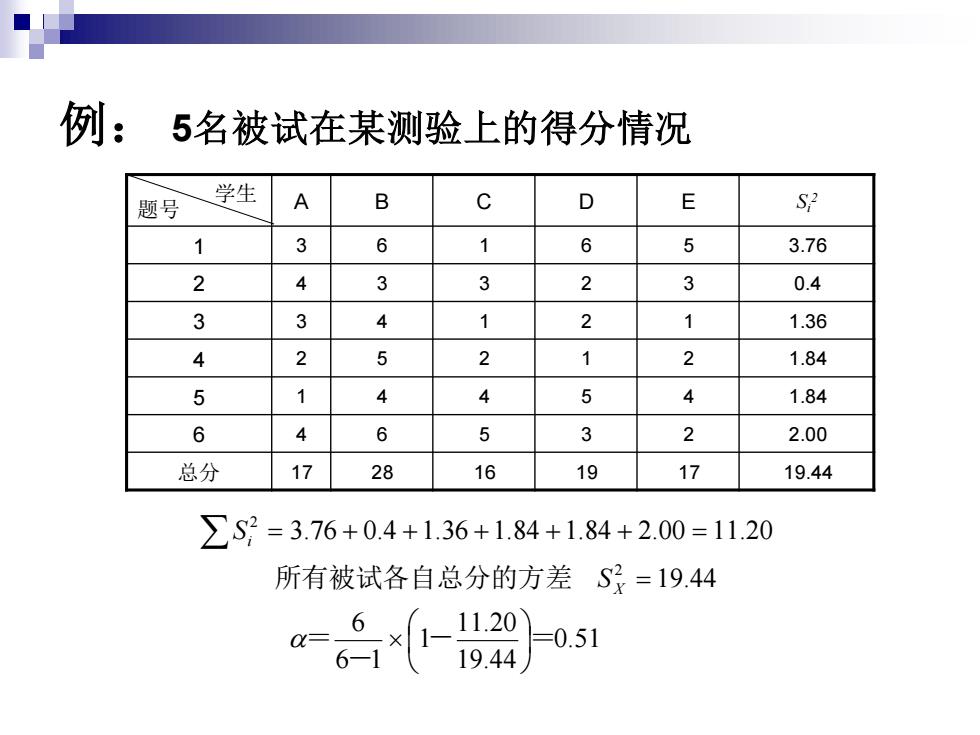
例: 5名被试在某测验上的得分情况 题号 学生 A B D E S 1 3 6 1 6 5 3.76 2 4 3 3 2 3 0.4 3 3 4 1 2 1 1.36 4 2 5 2 1 2 1.84 1 4 4 5 4 1.84 6 4 6 5 3 2 2.00 总分 17 28 16 19 17 19.44 ∑S2=3.76+0.4+1.36+1.84+1.84+2.00=1120 所有被试各自总分的方差S2=19.44 6 11.20 a- =0.51 6-1 19.44
例: 5名被试在某测验上的得分情况 A B C D E Si 2 1 3 6 1 6 5 3.76 2 4 3 3 2 3 0.4 3 3 4 1 2 1 1.36 4 2 5 2 1 2 1.84 5 1 4 4 5 4 1.84 6 4 6 5 3 2 2.00 总分 17 28 16 19 17 19.44 题号 学生 0.51 19.44 11.20 1 6 1 6 19.44 3.76 0.4 1.36 1.84 1.84 2.00 11.20 2 2 - = - = 所有被试各自总分的方差 = = + + + + + = X i S S